两个潜变量的模糊PLS-结构方程模型算法求解

任红梅，王 緌

（四川大学 工商管理学院，成都 610064）

0 引言

结构方程模型(SEM)方法是在20世纪70年代中期由瑞典统计学家Karl G.Joreskog提出的，受到了管理学界、心理学界等社会科学研究人员的青睐。这主要是因为它具有不同于一般统计分析方法的优点：（1）可以同时处理多个因变量；（2）允许自变量和因变量含有测量误差；（3）可以同时估计因子结构和因子关系；（4）允许更大的测量模型；（5）能够估计整个模型的拟合程度[1][2]。

结构方程现已在我国各个领域得到了广泛的应用，然而数据的输入都是采用确定的形式，从数据的来源看，结构方程的大多数数据是调查数据，通过设置问卷的方法获取。然而，这一过程中，存在着大量的不确定性因素。首先，备选答案之间存在中间过渡性，就具有模糊性；其次，在人类的感觉、判断、经验和情绪起重要作用的领域，本身存在大量的模糊性因素。考虑到大量的实际决策系统中,有时所获取参数信息不完全或者所获取信息的不可量化，Liu给出了模糊集的相关理论；文献[3]则研究了具有模糊参数的规划问题，并通过利用模糊集理论知识，给出了相应的算法。

不同模糊数据的可信性直接影响到结构方程模型结果的真实性，所以，将模糊变量引到结构方程模型，将一些边界不清，不易定量的因素转化了某种量化的表达形式，可以提决策的科学性与正确性。从结构方程数据获取的方式而言，选择模糊结构方程方法对模型中潜变量之间、潜变量与显变量之间的关系系数进行估计是一条可行也是一条较好的途径。本文拟采用模糊模拟[3]的算法，求解模糊PLS-结构方程迭代模型。该算法既保持了原结构方程的精华，同时又有许多良好的优化性能。

1 模糊PLS-结构方程模型

结构方程模型主要通过引入潜在变量来研究抽象变量之间的因果结构关系，由测量模型和结构模型两部分组成。PLS作为一种求结构解结构方程的“软模型”，可以明确求出潜变量估计值[4]，以及用PLS求解时不需要预先假设总体数据某种分布等。本文以2个潜变量的模糊PLS-结构方程进行研究并给出具体的求解过程。模型结构如图1。

图1 模糊结构方程模型

模糊PLS的结构方程模型由源结构关系和隐性结构关系组成。

1.1 源结构关系

源结构关系由两部分组成。

1.1.1 外部关系

其中：π1h0，π2k0为截距值；π1h，π2k为载荷系数；v1h，v2k为误差（残差）。

满足条件假设：（1）期望关系

（2）非相关性

1.1.2 内部关系

满足条件假设：E(η|ξ)=β0+β1ξ；r(ε,η)=0

1.2 隐结构关系

隐结构关系包括因果预测关系和权重关系，为偏最小二乘法分析所特有的。

1.2.1 因果预测关系

由（2）和（3）可得：

其中：截距为 μ2k=π2k0+π2kβ0

残差为 v2k=π2kε+v2k

满足条件假设：r(v2k,ξ)=0

1.2.2 权重关系

权重关系分为反映型和构成型两种模型，在图1中，潜变量η属于反映型，潜变量ξ属于构成型，其权重关系分别为：

2 模糊PLS-结构方程的求解

2.1 理论基础

设ξ为模糊变量，它的隶属函数是μ，如果u和 r是实数，那么一个模糊事件{ξ≤r}的可能性被描述为Pos{ξ≤r}，模糊事件{ξ≤r}的可信为 Cr{ξ≤r}Pos{ξ≤r}+1-Pos{ξ≤r})，在此基础上，Liu给出了模糊变量期望值的定义。

定义1 设ξ为模糊变量，则称

为模糊变量的期望值（为了避免出现∞-∞情形，要求上式两个积分到少有一个有限）。

那么，假设 f∶Rn→R 是一个实值函数，ξ=(ξ1，ξ2，…，ξn)是可能性空间(Θ，p(Θ)，Pos)上的模糊向量，则 f(ξ)也是一个模糊变量，它的期望值定义为

其中:L=Cr{f(ξ)≥r}为模型事件 f(ξ)发生的可信性,可以由下式估计得到：

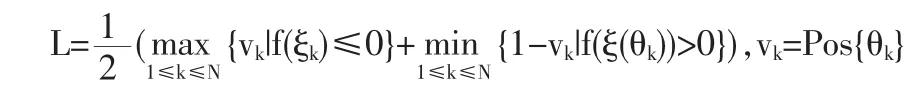
2.2 求解原理及步骤

对带有不确定数的数学模型，要进行计算，首先得转化化确定性问题的求解。从模糊数的特点不难判断，模糊PLS-结构方程模型的解不是唯一的，而是存在无数个，根据模糊数的性质，模糊数取不同值的隶属度一般不同，因此，由模型PLS结构方程得出的估计值和回归系数取不同解的可能性也一般不同。为了在目标值和可能度之间达到某种均衡或折中，我们引入模糊期望的概念，利用模糊模拟的原理，把不确定的数确定化，求解以上模型。由扩张原理知，由于所求的PLS 估计值 ω1h，ω2k，LXn，LYn都为的函数，记为 f,故都为模糊变量。

以两个潜变量的模糊PLS-结构方程的迭代模型为例，说明求解过程。该求解过程包括两大部分，一是运用模糊模拟的主程序；二是求解确定PLS-结构方程模型的迭代函数f，作为代求期望的模糊向量，向量中的各个元素的期望值即为待求的原结构方程的估计值。

2.2.1 模糊模拟

（1）置向量 e=0。

（2）分别从 Θ 中均匀产生 θk，使得 Pos(θk)≥ε，令 vk=Pos(θk)；k=1，2，…，N。 其中 ε 是个充分小的数。

(3)置向量 a=f(ξ(θ1))∧…∧f(ξ(θN))，向量 b=f(ξ(θ1))∨…∨f(ξ(θN))。

（4）从[ai，bi]中均匀产生 ri,构成向量 r。

(5)如果 ri≥0，那么 ei←ei+Cr{f(ξ)i≥ri}。

(6)如果 ri＜0，那么 ei←ei-Cr{f(ξ)i≤ri}。

(7)重复步骤（4）至步骤（6）共 N 次。

(8)E[f(ξ)i]=ai∨0+b∧0+ei(bi-ai)/N

2.2.2 确定PLS-结构方程模型的迭代原理

由模糊区间随机产生的数构成确定的输入数据。求解步骤如下:

这里f1,f2是标准化算子。 同理可得f2

重复以上步骤直到|ω（n）-ω(n+1)|＜10-5。

（2）由（1）步得出的潜变量估计值 LXn,LYn后,由以下几个方程估计出测量模型与结构模型系数

(3)将所求结果赋给函数f

3 模型应用

选取学生能力与成绩的一组小样本数据，对以上模糊PLS-结构方程模型进行测试。其中潜变量ξ为学习能力，η为学习成绩，其估计值分别为LX,LY。x1为IQ表现，x2为高中时综合成绩，x3为去年学习动机得分，y1为必修课平均绩点，y2为选修课平均绩点。由于IQ表现的程度之间本身就具有过渡性，且目前较真实的IQ测量需在失重的状态下进行才比较有效。根据相关资料和专家意见，对原始数据中x1进行模糊化 x1，为形如=(a1，a2，a3)的三角模糊数，见表 1。

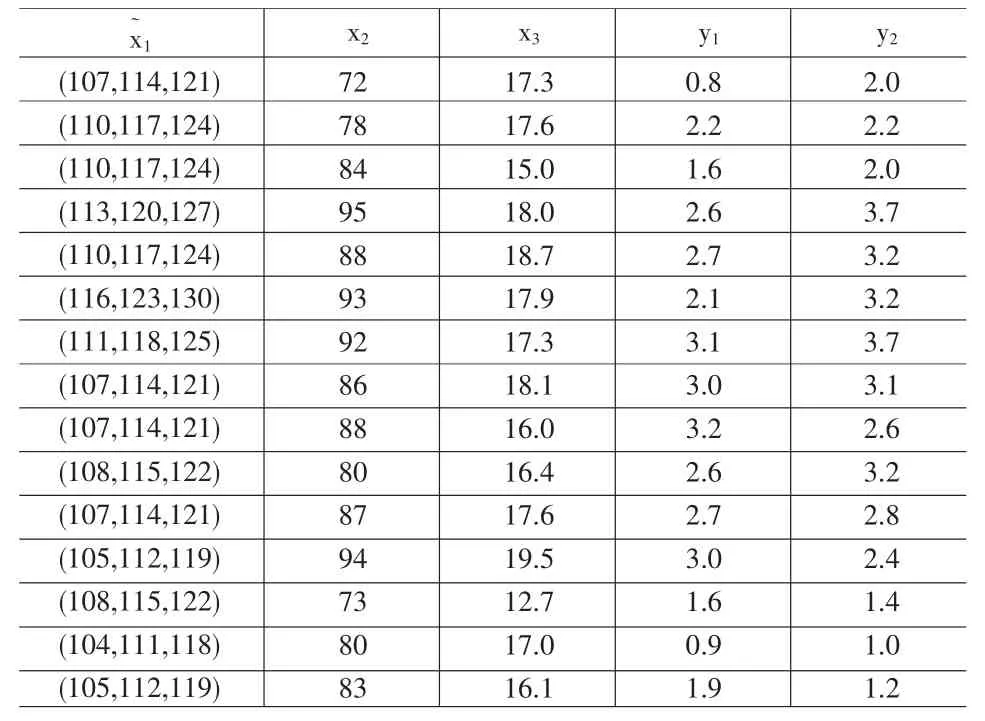
表1 模糊处理后的数据

表2 潜变量ξ与η的估计值LX与LY

表3 回归系数与拟合效果

在matlab7.0下,运用以上模糊PLS-结构方程模型实现程序,循环2000次,同时为了区别本文模型与传统确定的PLS-结果方程模型,将对比结果列入表2、表3。

从表3可知,当用确定PLS-结构求解时,由于忽略了大量模糊因素的存在,其结果与经过模糊化的PLS-结构方程有一定差别。当模糊数的置信水平取为1时,所有的模糊数都变成确定数—模糊数的主值,相当于应用确定PLS-结构方程模型。把IQ表现变量定义为三角模糊数时,与实际相吻合,得出IQ表现与学习能力的关系系数变小。

对回归方程进行显著性检验,确定PLS-结构方程模型R2=0.5692(越接近1越好)，拟合效果不是很好。如果此时我们把得出回归系数解释模型，必定不合理。相反，从模糊PLS-结构模型得出的结果可以看出，R2=0.6703＞0.5692，F=40.715＞＞F0.05(1,13)=4.67，因此，由x~1,x2,x3反映的 ξ与由 y1，y2反映的η之间线性关系显著存在；且在一定程度上优化了传统的确定PLS-结构方程模型。

4 结语

本文系统研究了含有两个潜变量的模糊PLS-结构方程模型的求解方法，给出了具体的求解步骤，并通过算例验证了模型有效性。由于目前结构方程的应用尚未直接引入模糊变量，对所有不确定变量的处理方式大多采用先确定化的方法，这种方式对以问卷获取输入数据为主要途径的结构方程模型而言是一个很大的弊端，将影响模型最终的解释能力。所以，本文的模糊PLS-结构方程模型方法为优化结构方程提供了一个有现实意义的数学工具；同时本文模糊模拟算法对含有两个潜变量的模糊PLS-结构方程具有普遍的适用性。考虑到实际中多个潜变量的情形，可结合该思想，对模型进行改进。

[1]侯杰泰，温忠麟，成子娟.结构方程模型及其应用[M].北京：教育科学出版社，2004.

[2]林盛，刘金兰，韩文秀.基于PLS-结构方程的顾客满意度评价方法[J].系统工程学报，2005，20(6).

[3]刘宝碇，赵瑞清，王纲.不确定规划及应用[M].北京：清华大学出版社，2003.

[4]宁禄乔，刘金兰.两个潜变量的PLS算法模拟数据分析[J].统计与决策，2007.(8).