基于半静态分层抽样的模糊聚类分析方法的改进
谢笑盈
(浙江工商大学 统计学院,杭州 310018)
0 引言
聚类分析是根据某种相似性度量将数据划分成有意义或有用的组,对聚类的研究源于对相似度的研究。随着研究的深入,聚类从最初的简单的数值型(包括离散的和连续的)数据以及逻辑型数据的聚类发展到对复杂的事务数据库的聚类,这其中对相似性的定义也发生了巨大的变化。在对数据对象分组过程中,其目标是组内的对象相互之间是相似的(相关的),而不同组中的对象是不同的(不相关的)。通常,组内的相似性越大,组间的差别越大,聚类效果越好。经常地,我们把组也称为簇。主要的聚类分析方法有划分方法、层次方法、基于密度的方法、基于模糊的方法等。本文将要讨论的是基于模糊的方法。
1 基于模糊的聚类方法
当数据集中的数据分布在明显分离的组中时,利用聚类算法,可以将数据对象明确地分到不相交的簇中,即,一个对象的所属的簇是非此即彼的。但在很多情况下,数据集中的对象不能划分成明显分离的簇,一个对象即可以划分到A簇,也可以划分到B簇,但可能离A簇稍微近一些,此时最好的解决办法是为该对象划分到A簇或B簇设置一个权值,指明该对象属于该簇的程度,即对象Xi以Wij的可能性属于Cj类。设置权值的方法可以用概率统计的方法,也可用模糊集理论的方法。基于统计模型的模糊聚类[1]就是利用概率统计为对象设置权值的一种方法。该方法假定数据是由一个统计过程产生的,并且通过找出拟合数据最佳的统计模型来描述数据,其中,统计模型用分布和该分布的一组参数来描述。更具体地说,就是可以把每个簇用一个合适的分布来表示,那么不同分布的对象自然要在聚类后被分开来,比较成熟的基于统计模型的模糊聚类方法是期望最大化(EM,expectation maximization)算法,它对参数做初始的猜测,然后通过迭代改进这些估计,直到参数不再改变为止。要使期望最大化可行,必须知道各个簇是满足什么分布,理论上应该首先考察各个对象所在簇的分布。但根据大量的统计事实,我们通常假定连续型数据对象是符合多元正态分布的,而离散型数据对象则多假定其满足泊松分布或二项分布。下面是对EM算法进行一定改进后的简要步骤:
(1)用DBSCAN[2]基于中心的聚类扫描一遍数据库,快速剔除离群点;
(2)为模糊聚类选择合适的统计分布组(比如一系列均值不相同的多元正态分布);
(3)选择模型参数的初始集合(比如多元正态分布中均值和方差);
(4)对于每个数据对象,计算该对象属于每个分布的概率(贝叶斯公式);
(5)得到(3)中所有数据对象的联合概率密度函数,并对其用最大似然法求出新的参数估计,更新(2)中的模型参数集;
(6)重复(3)、(4)、(5),直到参数不再改变为止。
EM算法利用各种类型的分布,可以发现不同大小和不同形状的簇,而且使聚类结果有很好的统计性质,这对于描述和理解数据都是非常有利的。但另一方面,因为EM涉及到复杂的运算,所有当对象的属性个数很多时,计算一个如此复杂的密度函数的最大似然值是不切实际的;另外,当簇只包含少量数据点,或者数据点之间有线性关系时,用该方法也不适合。最后,对于离群点和噪声,该方法也存在问题,上述部分改进后的EM算法克服了最后一个缺点,剔除了离群点和噪声,对另外两个缺点的改进将在后文中提出。
2 数据挖掘中的抽样技术
数据挖掘中应用的抽样技术主要来源于统计学中的抽样技术,但因使用目的和使用方式的区别,通常将数据挖掘中的抽样技术分为两类[3],即:静态抽样和动态抽样。静态抽样也称一阶段抽样或一次性抽样,是根据预先估计的误差范围、可靠性等计算一个固定的样本量,所有的后续分析只依据这一次性抽取的样本。该抽样方式一般在数据挖掘算法执行之前进行,适合各类挖掘任务的运用。数据挖掘的静态抽样方式都来自于统计抽样调查领域,主要有简单随机抽样、分层抽样、整群抽样。其中,简单抽样应用最广,分层抽样在分类问题中运用普遍,整群抽样在聚类时运用较多。比如,Heikki Mannila 等(1994)、Hannu Toivonen(1996)、M.Zakiand S.Parthasarathy(1997)、Einoshin Suzuki(2005), 都 运 用 一 次 性抽样方式挖掘了关联规则。静态抽样是从统计学的角度静态地判断样本与总体的近似程度。优点是实施比较方便。缺陷在于没有与挖掘工具结合起来,不能明智地回答样本是否足够好。
动态抽样指需要经过两次或更多次抽样才能达到最终要求的抽样方法,抽样过程与算法的执行过程和推断是交互进行的。它直接利用挖掘工具,能及时提供样本与总体接近程度的信息,而不是间接地考虑样本的统计特性。在该抽样方式下,决策者能够在算法效率和模型正确性之间及时做出抉择。数据挖掘中常用的动态抽样技术有累进抽样和序贯抽样,它们都可以称为适应性(adaptive)抽样。序贯抽样是数据挖掘中最早使用的适应性抽样方法,主要用于关联规则挖掘[4]和聚类分析。
Baohua Gu等在[5]介绍了一种独立于具体算法得最优样本容量的确定方法法,这个方法可归类于上文所提的静态抽样:用S.Kullback[6]的信息理论来描述抽样样本与总体数据集之间的信息差异Di,给Di和样本容量n做回归分析,当回归曲线的斜率接近于1时,说明样本容量n已达到了最优(OSS),此时的n即为最优样本容量OSS。结合该方法,本文使用下列算法来计算最优样本容量OSS:
(1)输入数据集D,其中包含N个实例;
(2)随机产生n个样本容量跨度在[1,N]区域中的样本Si,(i=1..n),[Si]表示样本 Si的样本容量并且满足/Si+1/=10*/Si/(i=1…n);
(3)计算每个样本Si在数据集D中的样本质量Qi;
(4)根据点(Si,Qi)的坐标拟合出一条样本容量和质量的曲线;
(5)输出 SOSS。
其中样本质量Qi的计算公式为为每个样本表示该数据集的属性个数,的每个样本的第i个属性有c种不同的取值,t表示总体,s表示样本,ptj表示总体中第i个属性的第j个取值的概率,psj表示样本中第i个属性的第j个取值的概率。
3 引入抽样技术后的改进的模糊聚类分析方法
在模糊聚类中运用抽样技术,通常的做法,是设计合适的抽样方案,提取一个样本,对样本中的点进行聚类;然后将其余的点指派到已有的离其最近的簇中。在抽样中,最可能犯的错误是因为抽样而丢失比较小的簇。当然,如果丢失的是噪声,就无所谓了。
在设计抽样方案时,为了使抽取的样本最大可能地反映总体的信息,本文结合静态抽样和动态抽样的优点,在参考最优样本统计量的基础上设计一种半静态抽样方法,具体算法如下:
(1)通过主成分分析或信息增益计算找到与挖掘任务关系最紧密的属性A,若用主成分计算时,A是第一主成分中系数最大的那个属性;若用信息增益计算时,A是使信息增益最大的属性(在数据量极大时,可用原数据集的一个随机样本来计算属性A,实验证明代表性较好);
(2)按 A 的值(a1,a2,…,an)对原数据集进行分组,各组的样本个数分别为N1,N2,…,Nn;
(3)计算最优样本容量OSS(前文已提);
(4)给每个组分配样本个数Si=OSSNi/N,得到最终的抽样样本
(5)在S上进行挖掘算法的挖掘。
该算法通过计算最具代表性的属性A,达到对数据集分层的目的,若选取主成分法寻找属性A时,可以克服属性间的线性相关问题。另外在选择了最优样本容量的基础上,通过对数据集的分层抽样增加了样本的代表性,使得抽样样本的特性最大可能地接近总体特性。
为了提高聚类的效率,我们还引进维归约的思想来加快聚类的速度。在高维数据集中(现实中的数据集大多是有十几个,几十个甚至上百个属性的高维数据集),考察对象邻近度的传统的欧几里得距离等概念变得不再适合。因为随着维数的增加,数据集构成的体积迅速增加(半径为r,维数为d的超球的体积正比于rd。),若数据集中点的个数很少,则其密度将趋向于0,那么各个数据子集的基于密度的邻近度度量将趋于一致,此时基于密度的聚类算法将不再适用。如果一个数据集的某一个子集拥有与之相同的簇的话,那么对该数据集维规约后的子集进行聚类就可以得到簇,当然这里的前提条件是重要的:数据集的聚类信息集中在少量几个属性上,其余属性是随机分布的。而要判断一个数据集是否满足这一条件并不是太困难的事情,只需对各个属性进行统计分析和信息分析就可以得出结果。将上述思想结合后得到引入抽样后的基于统计模型的模糊聚类的一个改进如下:
(1)对数据集进行统计或信息分析,剔除不必要的属性;
(2)对该数据集进行异常点的剔除;
(3)运用半静态抽样算法计算出样本集合S;
(4)对样本集S进行基于改进的统计模型的模糊聚类EM进行分析;
(5)对聚类结果进行评估。
4 实证分析
结合上述分析,选用UCI数据库中人口调查数据集为例,该数据集有32561条记录,将抽样方法引入EM模糊聚类,做出分析见表1。
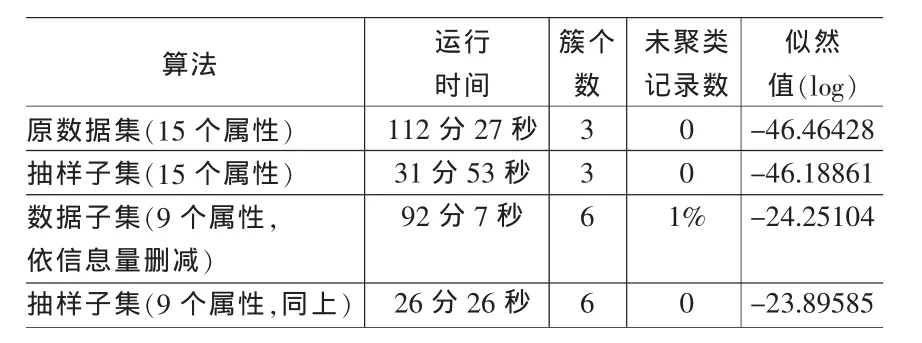
表1
从表1中可以清楚地看出EM算法因为要计算涉及所有属性的似然函数,并由此计算各个参数的值,所以运行速度非常慢,这也从事实上印证了前文对EM算法缺点的讨论:当涉及的属性个数较多,或数据集的记录条数很多时,EM的计算是不可行的。通过对属性的删减,可以减少部分运行时间,但聚类的结果有较大的不同,这说明在原数据集和它的子集上发现的感兴趣的簇可能是不一样的,这可能是因为剔除的属性中有影响簇个数的因子存在。另外,删减属性使得聚类结果在似然值上也发生了较大的改变,涉及的属性个数越少,似然值越大。
从抽样的结果看,无论在原数据集上的抽样还是在删除属性后子集上的抽样,都大大减少了聚类的时间,而且抽样并不影响结果中簇的个数,似然值也变化甚微。这说明抽样技术的应用在提高聚类效率的同时,还能保证聚类结果的一致性,是解决高数量级的数据集运算不可行的好办法。
5 结束语
虽然有学者提出在超大型的数据集上应用增量算法或分块处理来提高数据挖掘的效率可能比用抽样技术更有效,但在本文的实践过程中发现,对于中等数量级(几万到几十万数量级)的数据集,抽样技术有着其他技术不可比拟的优势——速度快,准确性高,易实现,特别是对于总体数据集有较好的统计特性时。今后,笔者将继续致力于研究统计方法与挖掘技术的结合。
[1]F.Hoppner,F.Klawonn,et al.Fuzzy Cluster Analysis:Methods for Classification,Data Analysis and Image Recognition[M].New York:John Wiley,1999.
[2]M.Ester.,H.P.Kriegel.,J.Sander.A Density Based Algorithm for Discovrerying Clusters in Large Spatial Databases with Noise[C].In Proc of the 2nd.Knowledge Discovery and Data Mining,1996.
[3]朱梅红.数据挖掘中抽样技术的应用[J].统计与决策,2007,(8).
[4]Tobias Scheffer,Stefan Wrobel.Finding the Most Interesting Patterns in a Database Quickly by Using Sequential Sampling[J].The Journal of Machine Learning,2000,8.
[5]Baohua Gu,Bing Liu,Feifang Hu,Huan Liu.Efficiently Determine the Starting Sample Size for Progressive Sampling[J].Lecture Notes in Computer Scierce,2001,2167.
[6]S.Kullback.Information Theory and Statistics[M].Chichester:John Wiley and Sons,1987.

