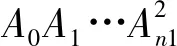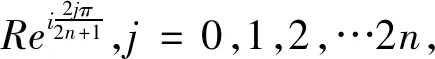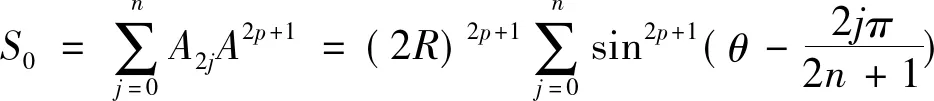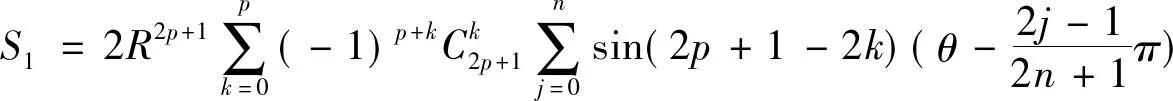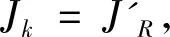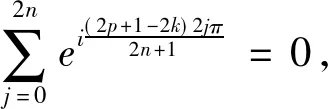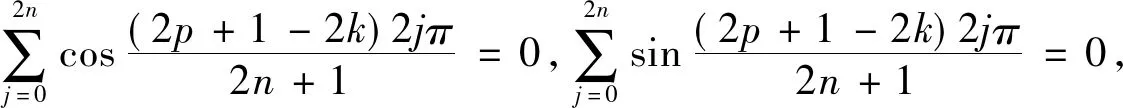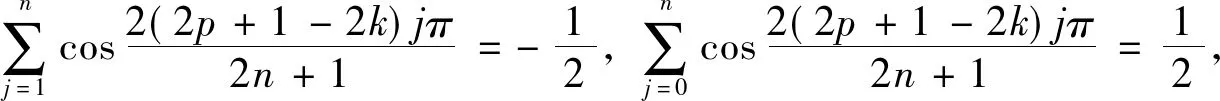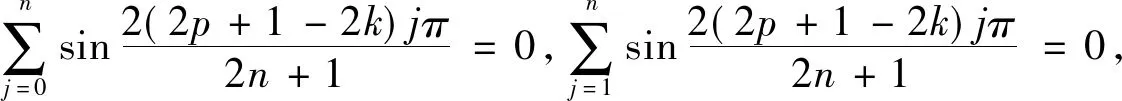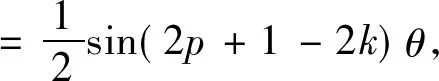圆内接正n边形的性质及应用*
沈 林 昌
(湖州市善琏成人文化学校, 浙江 湖州 313014)
1 引理
引理1 设m是整数,则
设p为正整数,下面的引理2引自文献[1]。

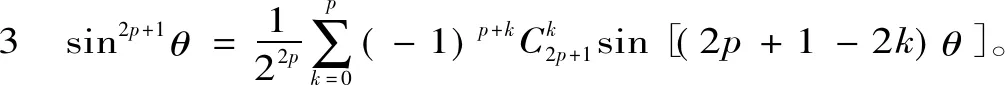
因此引理3成立。
2 主要结果证明
定理:设A是半径为R的正n边形A0A1…An-1的外接圆上任一点,p是正整数,且p 推论2 设正整数p A0A2p+1+A2A2P+1+…+A2nA2p+1=A1A2p+1+A3A2p+1+…+A2n-1A2P+1。 记S0=A0A2p+1+A2A2p+1+…+A2nA2p+1;S1=A1A2p+1+A3A2p+1+ …+A2n-1A2p+1 同时可证得: 但是 参考文献: [1] 熊喆风.圆内接正2n边形的一个性质[J].数学通讯,1988,(10):5-7.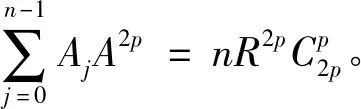
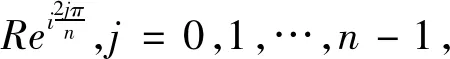
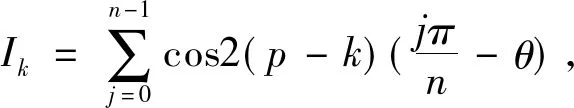
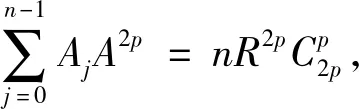

3 定理应用