基于振型分解反应谱法的重力坝抗震安全评价

黄宜胜 李建林 常晓林

(1.三峡大学水利与环境学院,湖北 宜昌 443002;2.武汉大学水资源与水电工程科学国家重点实验室,武汉 430072)

目前,工程界对于混凝土重力坝的抗震计算主要采用拟静力法和动力法两种[1].拟静力法是将结构的重力作用、设计地震加速度与重力加速度比值、给定的动态分布系数三者乘积作为设计地震力的静力分析方法.动力法包括振型分解反应谱法和时程分析法.时程分析法是由结构基本运动方程输入地震加速度记录进行积分,求得整个时间历程内结构地震作用效应的方法.振型分解反应谱法是先用反应谱法求解结构对应其各阶振型的地震作用效应后再组合成结构总地震作用效应的方法.根据《水工建筑物抗震设计规范(DL5073-2000)》的规定,工程抗震设防类别为甲类(场地基本烈度≥6度的1类壅水建筑物)时,地震作用效应的计算需采用动力法.作为线弹性结构的混凝土建筑物,可采用振型分解反应谱法或者振型分解时程分析法.由于采用振型分解反应谱法进行混凝土重力坝抗震计算相对简单易行,因此该法是采用最多的动力计算方法.

正在建设中的金安桥水电站位于云南省丽江市境内的金沙江中游河段,是金沙江中游河段规划的“一库八级”电站中的第5级.该电站大坝为碾压混凝土重力坝,正常蓄水位为1418 m,坝顶高程为1424 m,最大坝高为160m,坝顶长度为640m.大坝左岸坡坝段坝基岩层倾向河床,坝基为台阶状,坝基岩体多为碎裂和块裂绿泥石化岩体,如图1所示,且大坝抗震设防烈度高达Ⅸ度,这些因素导致左岸坡坝段在地震作用下比较危险,因此非常有必要利用动力分析方法对左岸坡坝段进行抗震安全评价.由于金安桥水电站碾压混凝土重力坝横缝结构为间断式横缝,因此大坝可近似为一个整体,经与设计单位协商,确定采用振型分解反应谱法对由④、⑤、⑥坝段组成的左岸坡坝段群进行抗震安全评价[2].

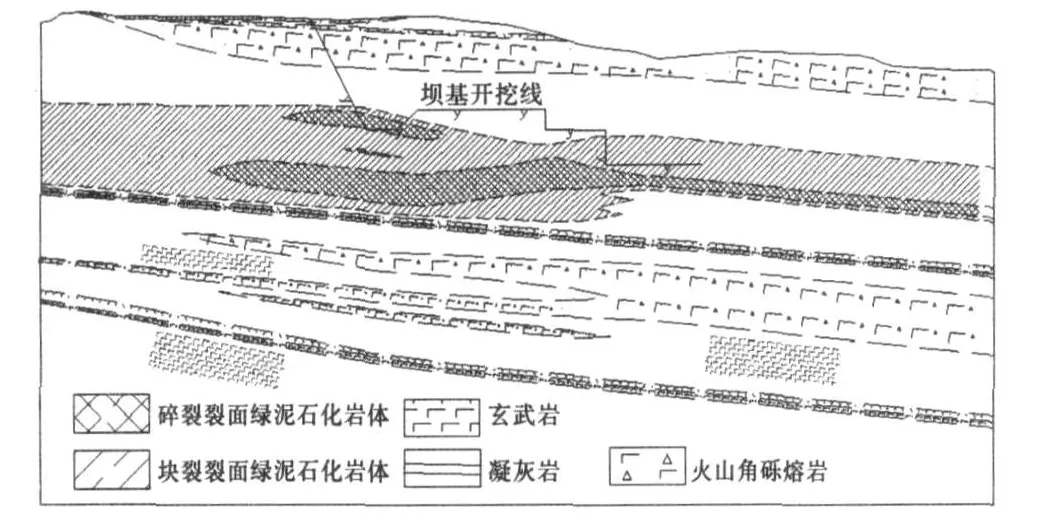
图1 ④、⑤坝段交界横缝处地质纵剖面图

1 重力坝静动应力叠加原则

振型分解反应谱法计算的只是重力坝在动力作用下的位移与应力,当对重力坝进行抗震安全评价时必须对静力作用下的位移与应力和动力作用下的位移与应力进行叠加.由于振型分解反应谱法计算出的位移与应力均为绝对值,而静力作用下的位移与应力却是有正有负,因此如何进行静动叠加是重力坝抗震安全评价时首要解决的问题.规范(DL5073-2000)规定,当对重力坝进行抗震安全评价时只需大坝的抗震强度和稳定性满足承载能力极限状态设计式的要求,因此本文重点探讨的是重力坝在地震作用下的静动应力叠加原则.目前关于静动应力叠加原则的相关文献较少,文献[3]介绍了静动应力叠加的两种原则,即最不利组合原则和全拉全压原则;文献[4]提出了应力同向或者反向直接叠加原则,同向叠加为动态位移与应力和静态位移与应力同号的代数和,反向叠加为动态位移与应力和静态位移与应力反号的代数和.另外很多文献只是给出了静动应力叠加的结果,没有明确静动应力叠加的原则[5-6],有的甚至不进行静动应力叠加[7-9].总的说来,目前的静动应力叠加原则基本上可概括为两类,即:间接叠加原则和直接叠加原则.

1.1 间接叠加原则

其叠加原则为:对于坝体同一结点,如果静应力分量为负,且该部位的动应力相应分量数值小于其静应力相应分量的绝对值时,那么把该动应力分量作为负值与静应力相应分量进行叠加;在其他情况下(包括静应力分量为负时,且该部位的动应力相应分量数值大于其静应力相应分量的绝对值和静应力分量为正时两种情况),把动应力相应分量直接与静应力相应分量叠加.由于要根据静动应力分量的符号以及大小对比结果来决定叠加方式,因此把上述叠加原则称为“间接叠加原则”.

1.2 直接叠加原则

考虑到按间接叠加原则得到的坝体综合应力并不一定是大坝的最不利情况,如把地震作用下的各个动应力分量都作为正值直接与静应力相应分量叠加,可能对大坝来讲更加危险.因为根据振型分解反应谱法计算得到的动应力各分量均为绝对值,基于上述应力叠加原则,铅直向动应力的效应相当于在大坝建基面上起到全断面上抬的作用,这大大减小了大坝抗滑稳定的抗力,而水平向动应力也可能对水平向滑动效应起到加强的作用.由于该原则把静动相应应力直接叠加,因此把上述叠加原则称为“直接叠加原则”.

2 抗震计算方法

在进行抗震计算时,假定坝体是线弹性体,地基为弹性无质量体[10].库水对坝的动力作用可等效为附加质量,附加质量采用Westergaard公式计算.坝体自振特性采用子空间迭代法,动力分析采用振型分解反应谱法.同时考虑三向地震的作用,计算中提取前10阶振型,各振型之间采用SRSS方法组合,即取各阶振型地震作用效应平方总和的方根作为总地震作用效应.地震作用下总作用效应为动力作用效应与静力作用效应按最不利原则叠加而成.

规范(DL5073-2000)规定,水工建筑物的抗震强度和稳定应满足下列承载能力极限状态设计式

当评价重力坝的抗滑稳定性时,可令

则K可看作规范(DL5073-2000)里的动抗滑稳定安全系数,只要K≥1就可满足规范要求(上式中各符号含义及取值详见规范(DL5073-2000)).

3 工程基本资料

3.1 地震参数和材料参数

依据规范(DL5073-2000)规定,金安桥水电站坝址区域为Ⅰ类场地,特征周期为0.20 s,设计反应谱最大值的代表值为2.0;地震设计烈度按Ⅸ度取值,水平向设计地震加速度代表值为0.4 g,竖向设计地震加速度的代表值取为水平向设计地震加速度代表值的2/3;混凝土动态强度和动态弹性模量的标准值在其静态标准值基础上提高30%,混凝土动态抗拉强度的标准值取为动态抗压强度标准值的10%,基岩动态变形模量也较其静态提高30%,动态抗剪断指标等同静态值;重力坝的恒定阻尼比取为5%.

表1～2分别为金安桥水电站大坝混凝土和坝基岩体的物理力学参数.

表1 金安桥水电站大坝混凝土物理力学参数

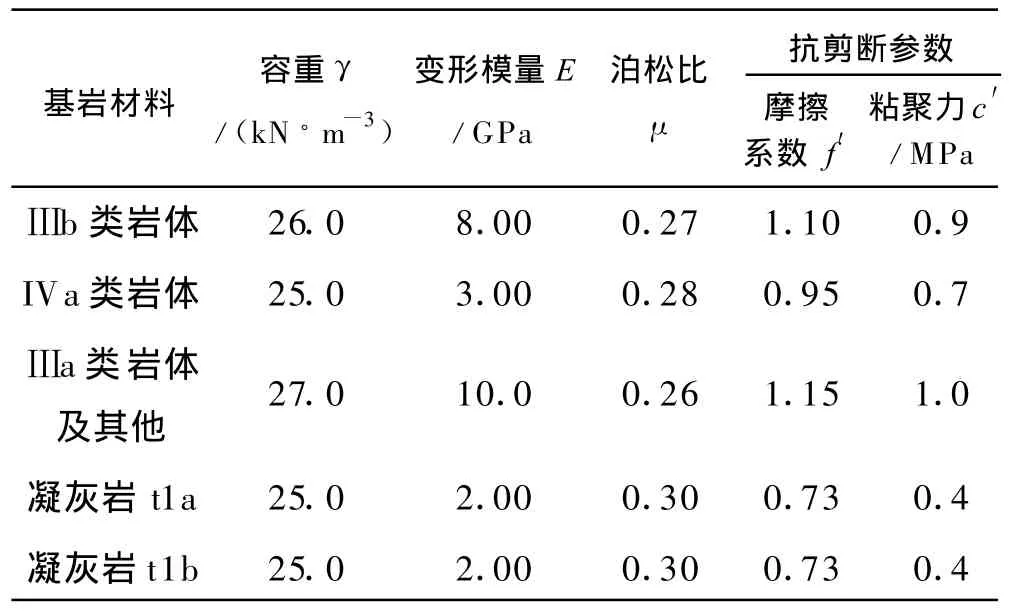
表2 金安桥水电站大坝坝基岩体物理力学参数

3.2 计算荷载和材料模型

静力计算所施加的荷载为:上游正常蓄水位水压力+下游相应尾水位水压力+坝体自重+上游淤沙压力+坝基面扬压力,最大水压高度为130 m;动力计算只考虑地震荷载.对于大坝和坝基,静动计算均采用线弹性本构模型.

3.3 有限元模型

金安桥水电站左岸坡坝段群的计算模型由④、⑤、⑥3个坝段组成,如图2所示.模型详细模拟了坝体的材料分区和基本体型.坝基部分则主要模拟了玄武岩、软弱岩层及两种绿泥石化岩层.坝基计算范围为:基础深度最低取为1.5倍坝高(这里的坝高是指⑥坝段的最大坝高),即204m;自坝轴线向上游取为1.5倍坝高;自⑥坝段基本体型的最低坝趾处向下游取为1.5倍坝高.模型网格以八节点六面体单元为主,局部部位采用五面体单元进行过渡.由于大坝切割式横缝很薄,故采用薄层单元来模拟横缝.为了考虑混凝土横缝的开裂对坝体抗震性能的影响,计算中把横缝薄层单元弹性模量折减为原来的60%.整个模型单元数为10039个,节点数为11759个,其中坝体单元数为2670个,节点数为3436个.另有312个上游坝面附加质量单元,附加质量单元采用质量单元来模拟.坝体左右面不施加约束,当作自由面处理;坝基上下游面、左右面和底面,施加垂直向约束.

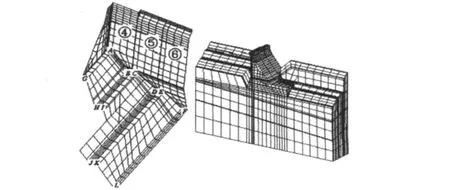
图2 左岸坡坝段群以及整体网格图

静、动计算用到的有限元模型均是图2的模型,唯一的区别在于附加质量单元只在进行动力计算的时候才会用到.质量单元是一个点单元,当进行动力计算时,需把质量单元附加在上游坝面与水接触的节点上,故又称该单元为附加质量单元,本次计算采用的是ANSYS里的MASS21质量单元.在计算过程中,先通过Westergaard公式计算上游坝面水下节点处的附加质量,然后再把这个附加质量输入到质量单元的实常数中,这样就完成了附加质量单元的设置.

4 抗震安全评价

4.1 强度评价

分别按间接叠加原则和直接叠加原则进行静动应力叠加,然后进行强度评价,叠加结果如图3～4所示.坝体应力计算结果表明,无论是在静力作用下还是在动力作用下,金安桥水电站左岸坡坝段群的坝体应力沿坝高分布都比较均匀,但坝踵与坝趾处均存在应力集中现象,故抗震强度评价只需评价坝踵与坝趾处强度.坝踵处评价抗拉强度,坝趾处评价抗压强度.对于坝踵处,依据上述两个叠加原则,可知评价结果都是一样的,见表3,但坝趾处的评价结果有较大差异,见表4～5.表中“√”表示满足式(1),“×”表示不满足式(1).

图3 静动应力间接叠加后竖直向应力分布图

图4 静动应力直接叠加后竖直向应力分布图

表3 金安桥水电站左岸坡坝段群坝踵抗震强度评价(单位:MPa)

表4 按间接叠加原则进行坝趾抗震强度评价 (单位:MPa)

表5 按直接叠加原则进行坝趾抗震强度评价 (单位:MPa)

由表3～5可知,左岸坡坝段群坝踵处的拉应力超过了规范(DL5073-2000)的极限承载能力要求,而坝趾处的压应力则满足极限承载能力要求.众所周知,在有限元分析中,坝踵、坝趾处的应力集中现象非常复杂,应力集中的数值和区域与该部位的单元种类、单元形态、网格疏密程度有关,另外也受坝体与坝基的刚度以及计算方法等多种因素的影响.尽管坝踵、坝趾处的应力集中现象比较突出,但实际上岩体中的微细裂隙和混凝土本身的塑性特性可对这种应力集中现象起到比较明显的缓解作用,因此坝踵、坝趾处的实际应力应该小于计算值,而且由于坝踵处拉应力区范围较小,小于坝底宽的7%,故可认为坝踵坝趾处的应力集中不致于影响大坝的抗震安全.

另外,从表4～5可知,虽然按上述两种叠加原则进行坝趾抗震强度评价均能够满足规范(DL5073-2000)的极限承载能力要求,但显然按间接叠加原则要比按直接叠加原则进行坝趾抗震强度评价的结果要危险一些,故间接叠加原则一般又可称为“强度最不利应力叠加原则”.因此,为偏安全计,当对重力坝进行抗震强度评价时,需对静动应力叠加采用强度最不利应力叠加原则.

4.2 动抗滑稳定评价

对于坝基为台阶式的碾压混凝土重力坝岸坡坝段来说,当遭遇地震作用时,大坝不只是具有顺河向的滑动趋势,同时也具有横河向的滑动趋势,因此总的作用效应应为顺河向和横河向的作用效应的矢量和.本文中SX(*)为顺河向作用效应,SY(*)为横河向作用效应,S(*)为顺河向和横河向总的作用效应,β为总的作用效应与顺河向的夹角.对于各坝段建基面的抗剪断指标,取坝基混凝土与各坝段基岩接触面积的加权平均值.

从表6～7可知,无论是按间接叠加原则还是按直接叠加原则进行静动应力叠加,金安桥水电站左岸坡坝段群和单个坝断的抗震稳定性均满足规范(DL5073-2000)的极限承载能力要求.因此,金安桥水电站左岸坡坝段群和单个坝段在设防烈度为Ⅸ度的地震作用下能够保持稳定.

表6 按间接叠加原则进行抗滑稳定评价 (106kN)

表7 按直接叠加原则进行抗滑稳定评价 (106kN)

另外,从表6～7可知,显然按直接叠加原则要比按间接叠加原则得到的重力坝动抗滑稳定安全系数要小一些,故直接叠加原则又可称为“稳定最不利应力叠加原则”.这说明从偏安全角度来讲,当对重力坝进行抗震稳定性评价时,需对静动应力叠加采用稳定最不利应力叠加原则.

5 结 论

(1)振型分解反应谱法计算出的位移与应力均为绝对值,而静力作用下的位移与应力有正有负,因此如何进行静动叠加是重力坝抗震安全评价时首要解决的问题,目前的静动应力叠加原则基本上可概括为强度最不利应力叠加原则和稳定最不利应力叠加原则.

(2)为偏安全计,当对重力坝进行抗震强度评价时,必须对静动应力叠加采用强度最不利应力叠加原则;当对重力坝进行抗震稳定性评价时,必须对静动应力叠加采用稳定最不利应力叠加原则.

(3)金安桥水电站左岸坡坝段群在Ⅸ度地震作用下,坝踵坝趾处的抗拉、抗压强度和单个坝段、坝段群的抗震稳定性均满足规范(DL5073-2000)的要求,这说明金安桥水电站碾压混凝土重力坝能够抵御设防地震.

[1］倪汉根,金崇磐.大坝抗震特性与抗震计算[M].大连:大连理工大学出版社,1994.

[2］孙恭尧,王三一,冯树荣.高碾压混凝土重力坝[M].北京:中国电力出版社,2004.

[3］张传国.Ansys在混凝土重力坝振型分解反应谱分析中的应用[J].云南水力发电,2009,25(6):24-28.

[4］焦爱萍,刘宪亮,许新勇.宝泉浆砌石重力坝三维有限元动力分析[J].水利水运工程学报,2007(1):36-40.

[5］杜成斌,洪永文.带有参数不确定性的重力坝地震响应的直接数值模拟[J].世界地震工程,2006,22(3):46-52.

[6］张晓燕,任旭华,邵 勇.碾压混凝土重力坝陡峭建基面的动力稳定分析[J].红水河,2007,26(4):35-38.

[7］刘国明.古田溪一级重力坝悬臂梁振型分解反应谱法抗震计算[J].水力发电学报,2004,23(1):31-35.

[8］汪家正,阎贵平.基于ANSYS的重力坝地震动力有限元分析[J].华北水利水电学院学报,2006,27(1):21-23.

[9］张晓燕,任旭华,邵 勇.软弱夹层对碾压混凝土重力坝的动力影响分析[J].中国农村水利水电,2008,94-97.

[10]Coulgh R W,Cheng K T,Chen Houqun,et al.Dynamic Interaction Effects in Arch Dams Report No.EERC-85/11[R].Berkeley:Earthquake Engineering Research Center,University of California,1985.