基于状态空间法的复杂正弦稳态电路相量计算

袁新娣，黄贤通

（1. 赣南师范学院 物理与电子信息学院，赣州 341000；2. 赣南师范学院 数学与计算机科学学院，赣州 341000）

基于状态空间法的复杂正弦稳态电路相量计算

袁新娣1，黄贤通2

（1. 赣南师范学院 物理与电子信息学院，赣州 341000；2. 赣南师范学院 数学与计算机科学学院，赣州 341000）

0 引言

如图1[1]所示的四网孔正弦电路是大型复杂电路系统的代表。该电路的特点是所含储能元件多，电路阶数高，电路结构比较复杂，所以对该类电路的分析有较大的代表意义。为了全面地反映一个电路系统的内在运动规律，通常会通过建立系统的状态空间表达式数学模型，但在正弦电路的稳态分析中，通常需要求出该稳态输出的相量表达式。本文应用MATLAB软件，通过系统的状态空间表达式模型，计算获取了系统的正弦稳态电流响应的相量表达式，同时本文也应用传统的稳态电路相量分析法验证了该方法的正确性。

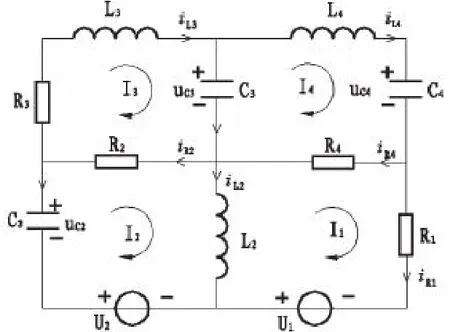
图1 四网孔正弦电路

1 由状态空间法获取稳态电流响应相量

1.1 四网孔正弦电路的状态空间表达

状态空间法是建立在状态变量描述基础上，揭示控制系统内在运动规律的一种时域分析方法。用状态空间法建立系统数学模型称为状态空间描述，用状态空间表达式表征[3]，状态空间表达式通常有两个数学方程组成：

其中方程(1)是反映系统内部状态变量X和输入变量u间因果关系的数学表达式，常具有微分方程或差分方程的形式，称为状态方程；方程(2)是表征系统内部状态变量X及输入变量u和输出变量y之间转换关系的数学表达式，具有代数方程的形式，称为输出方程。

根据电路的状态空间理论[4]，对于图1，应选取电感电流i12,i13,i14及电容电压uc2,uc3,uc4作为内部状态变量，两电源u1与u2是电路的输入变量，对图1电路可以建立如下状态方程：

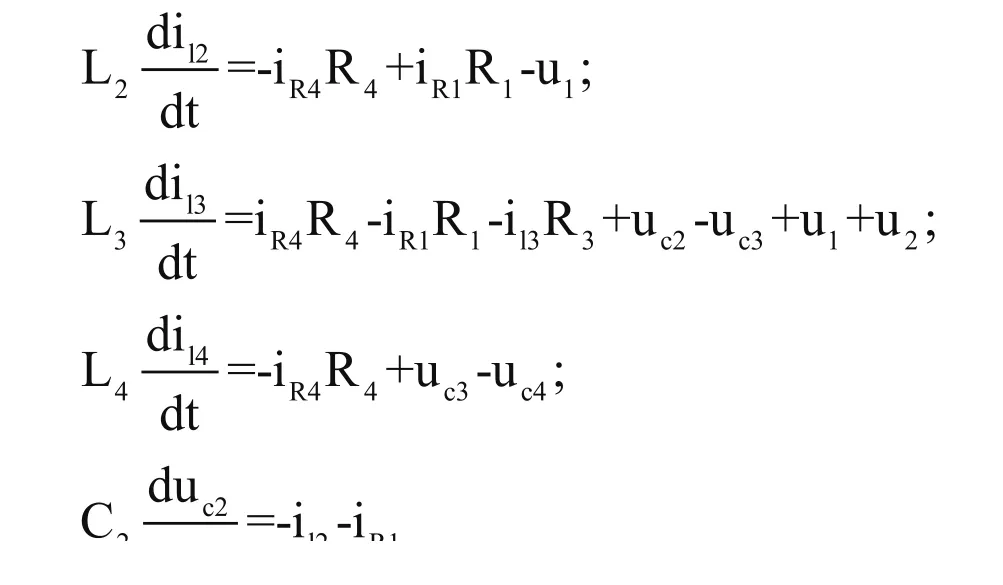
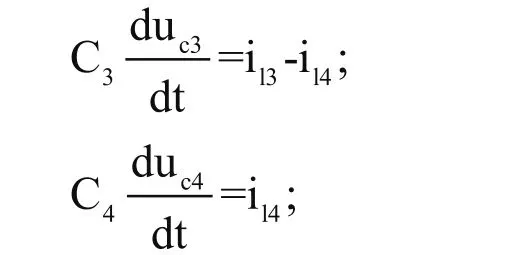
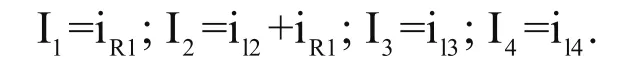
再根据基尔霍夫电压定理（KVL）和基尔霍夫电流定理（KCL）得到下面方程组：

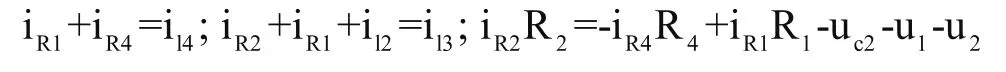
利用该方程组消去状态方程和输出方程中的中间变量iR2,iR3,iR4后就可以得到图1系统的状态空间表达式：

1.2 MATLAB 软件获取稳态电流响应相量

在电路各元件的参数已知的情况下，可以根据表达式(3)应用MATLAB软件计算获取电路的稳态网孔电流相量。现通过下述实例来说明这点。

例1：在图1表示的四网孔电路中，已知L2=L3=L4=0.0 0 3 H；C2=C3=C4=0.0 0 3 F，R1=R2=R3=R4=1Ω,激励电源U1=cos(314t)，U2=1.2cos(314t)。即已知所有元件参数及输入激励，求网孔回路的稳态电流相量。

把电路各元件参数代入状态空间表达式(3)中的G、A、B、C、D得到状态方程和输出方程分别为：

利用MATLAB解状态空间方程时，可以使用指令[I ,t]=lsim(ss1,[u1;u2],t)获得电路在对应激励作用下的电流响应波形，其中ss1是该系统的状态空间表达式，u1,u2是输入激励，t是指定的仿真时间序列，I是返回的网孔回路电流响应序列值。指令执行结果如图2所示。下面将分析如何从图2所示输入输出波形中获得稳态网孔电流的相量表达式。

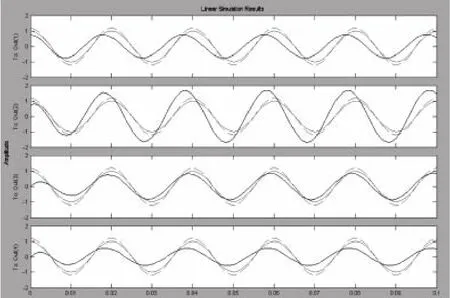
图2 按例1所设计的参数情况下的输入及各网孔电流输出波形

因为各网孔的稳态电流是与激励电源频率相同、但幅值和相角可能不同的正弦信号，所以要获得正弦电流稳态表达式只需求出各网孔稳态电流的幅值和初相角，而幅值就是各网孔电流的仿真序列的最大值，初相角是指网孔电流的相位与相应激励源的相位之差。所以应用MATLAB编程获取稳态相量表达式时的具体做法是：

1）用max指令获得各个网孔回路电流的最大值，也就是相量的幅值；

2）从各输出波形图中取某个稳定时刻的电流值和同一时刻的激励输入电源值，利用acos指令获得该时刻电流的相位和电源的相位。注意：因acos函数返回值的范围是[00,1800],且在取值范围内该函数是降函数，该例中的电源初相角又是零，所以这个稳定的时刻不是随便取，在该时刻，网孔电流应当已经达到了稳定，且电源与网孔电流的波形都同为下降。本文选择了第64个仿真时刻来计算网孔回路电流初相角；

3)把上述获得的网孔电流的相位与电源的相位相减，这样就获得了相应网孔回路电流相量的初相角。

根据上述论述，设计的M A T L A B程序如example1.m[5]。

从运行结果可知，按例1所提出的参数计算出的四个网孔的回路电流相量为:

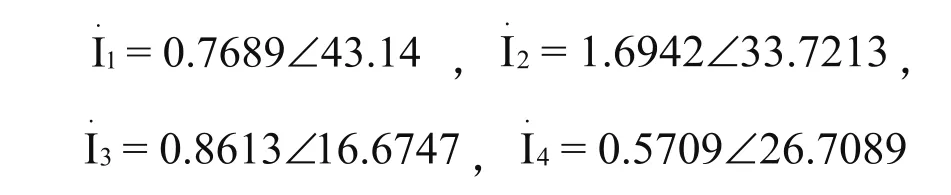
2 用相量分析法获取电路的回路电流相量

为了验证上述应用状态空间表达式结合MATLAB进行的稳态电路相量分析的正确性，下面对例1应用传统的相量分析法分析计算回路电流相量。

相量法就是用一个复数(X)来表示一个正弦量，复数的模是正弦量的有效值或幅值（本文采用幅值），复数的相角是正弦量的初相角。相量分析法的原理见参考文献[4]。图1所示的电路在正弦信号作用下，可以根据相量分析法的回路电流法建立相量方程(4)[4]：

对比前述的状态空间分析法分析得到的结果，相差不到2%，而这个误差大小是工程上认可的，从而说明了本文采取的状态空间表达式结合MATLAB软件分析复杂电路稳态响应相量的方法是正确的。

3 结论

本文研究了状态空间表达式结合MATLAB分析计算复杂电路——四网孔正弦稳态电路的网孔回路电流相量响应，同时，为了说明该方法的正确性，对同一实例的同一问题也应用了传统的相量分析法分析计算，两次计算结果的一致性说明了本文提出的计算方法是有效的、可靠的。

[1]Liu Jian-sheng.The Application of Matrix Theory in Second Order Electrical Circuits Designing. Proceedings of the Eighth International Conference on Matrix Theory and Its Applications in China, Advances in matrix theory and its applications[C],series B(2008):202-205.

[2]陈建业.电力电子电路的计算机仿真[M].北京:清华大学出版社,2003.

[3]胡寿松.自动控制原理(第四版)[M].北京:科学出版社,2000.

[4]邱关源.电路(第五版)[M].北京:高等教育出版社,2006.

[5]张志涌.MATLAB教程[M].北京:北京航空航天大学出版社,2002.

Phasor-analysis about complex circuit base on state-space

YUAN Xin-di1, HUANG Xian-tong2

四网孔正弦电路是大型复杂电路系统的代表，其稳态电流相量的分析计算是性能分析的的重要方面。本文研究了一种新的方法，即利用能够描述系统内部特性的状态空间方程，同时结合MATLAB软件对电路的稳态电流相量进行分析计算。为了验证该方法的正确性，本文也应用传统的相量分析法对同一实例的相同输出进行了求解。两次求解结果的一致性，说明了本文研究的方法在求解正弦稳态电路的相量上是有效的、可靠的。

四网孔正弦稳态电路；分析；相量；状态空间法

袁新娣（1974－），女，江西瑞金人，硕士，主要从事电子信息方面教学与研究工作。

TP391

B

1009-0134(2010)06-0091-04

10.3969/j.issn.1009-0134.2010.06.31

2009-11-30