一种改进的威胁空间搜索算法

杜思翰, 李 铭



一种改进的威胁空间搜索算法

杜思翰1, 李 铭2

(1.湖南大学 软件学院, 湖南 长沙，410082; 2. 湖南文理学院 土木工程学院, 湖南 常德, 415000 )

研究了五子棋游戏开发中极大极小搜索框架计算量太大, 无用计算太多等问题. 在传统经典极大极小搜索和alpha-beta剪枝基础上采用了判重, 加入启发式的优化, 每次选择最有“前途”的若干个决策搜索以减少搜索量, 再加入基于五子棋专业棋手下棋策略, 改进威胁空间搜索算法. 使得计算机的搜索过程更像人的思考过程, 算法复杂度大幅降低. 经过测试最终编写的程序具备高响应度和智能性.

极大极小搜索；alpha-beta剪枝；判重；启发式；威胁空间搜索

五子棋的算法发展了多年, 先后有基于深度优先敌对搜索的极大极小搜索[1-2], 优点是编程复杂度低, 但是计算量太大无法接受. 之后伴随着alpha-beta剪枝[1-2]的出现搜索量有了显著的减小, 对于connect-four和tic-toe-tac等游戏已经能很快的完美解决. 但是由于五子棋搜索的branch-factor(分枝因子)太大(平均约为200). 所以还是不能高效地解决五子棋. 之后出现的SSS*[3]基于广度优先搜索的框架将搜索量进一步减小, 但由于空间复杂度太高一直没有得以应用. 之后伴随着算法的进一步发展, proof-number search[4]和遗传算法[4]等从根本上改进算法复杂度的优秀算法出现了. 但这些算法的共同特点是编程复杂度太高和不成熟, 使得它们也没有广泛地应用起来. 五子棋真正的优秀算法, 是要在编程复杂度、时间复杂度、空间复杂度上得到一个极好的平衡同时能够保证搜索质量. 笔者在极大极小搜索和alpha-beta剪枝加入了判重[5]、启发式加权排序[6]、威胁空间搜索.

判重能够避免重复搜索, 而启发式加权排序能够同时提高alpha-beta剪枝的效果和进一步减少无用搜索. 为了更好地提高效率和智能, 引入了威胁空间搜索. 在每次搜索前调用一个复杂度较小的：“二次搜索”来减少无用计算.

1 判重

如图1所示的搜索树, 数字代表状态编号, 由于该极大极小搜索采用深度优先实现, 所以会做很多重复的搜索. 如图1, 设搜索的结点顺序为1→2→4→5→3, 而假设3之后的局面为4, 5, 那么这时可以发现4和5在之前已经搜索过的, 不需要再次搜索. 所以产生了重复计算. 故可以保存每次搜索之后的结果, 这样下次访问该节点时若已经搜索过直接取结果. 事实上经过如此改造, 搜索的图形其实已经变成了一个有向无环图(dag, directed acycl- elic graph), 满足无后效性质, 搜索的本质变成了动态规划. 一颗搜索树经过判重改造后如图2所示.

图1 一颗搜索树

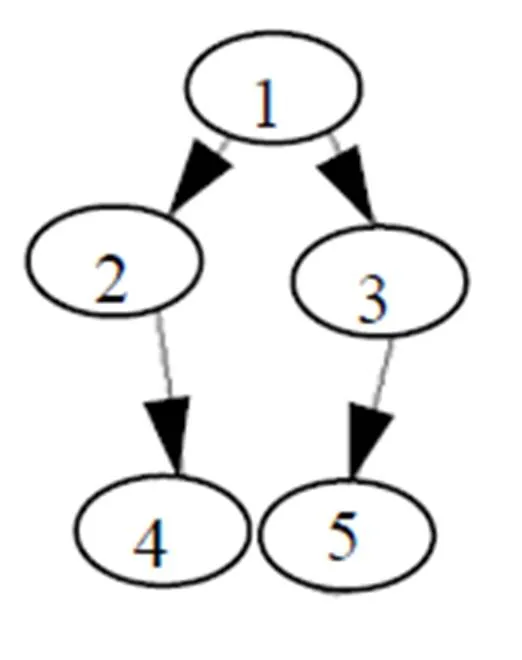
图2 改造后的dag

这样搜索量将会大减, 判重实现可以采用平衡树((logn))或者rk等hash算法(期望复杂度(1)), 或者采用字典树, 每个状态最多只有3个子结点, 也可以针对实现的语言调用相关的模板库(如C++就可以用stl).

2 启发式的应用

首先从游戏本身着手优化, 加入经典的五子棋棋谱. 类似于围棋, 五子棋也有很多经典棋谱, 若将若干棋谱建造一个“数据库”, 则当前残局如果在数据库中, 马上选择相应的对策.

加入人下棋时候的基本策略：

a. 如果某个位置能让自己获胜那么马上选择该位置；

b. 如果某个位置对手能够一步获胜那么必须阻止；

c. 如果某个位置对手有诸如.BBBB.这样的连线, 那么本局是必败局. 所以如果对手可能造成这样的局面, 必须要阻止.

还有其他策略诸如下棋的时候一般会尽量选择靠近棋盘中央的空区域, 尽量让自己“一举多得”. 连线加权概念：

a. “WBBBB.”, “B.BBB.”算做第1类,记8分；

b. “WBBB.”, “B.BB.”算做第2类, 记3分；

c. “BB.”, “B.B”算做第3类, 记1分.

放置棋子时, 希望其所在的4个方向(水平, 竖直, 主对角线, 副对角线)得分之和尽可能多, 且尽量靠近中间棋盘. 所以将决策排序, 第1关键字分数从大到小, 第2关键字与棋盘中央的迈哈顿距离从小到大. 可以更好的发挥alpha-beta剪枝的作用. 同时可以只搜索排序后靠前的几个决策, 根据是基于这样一个假设：在当前阶段看似没有“前途”的决策很难产生比看似更有“前途”的决策更好的最终结果.

3 威胁空间搜索

威胁空间搜索是模拟人对于“威胁”这个概念的对策以及从五子棋本身的特点入手进行优化, 将棋手下棋中的套路公式化提高搜索效率.

3.1 相关定义和知识

在五子棋中, 威胁是一个重要的概念；主要种类的名字：four(图3a)是5个方块, 第5个方块位置为空；straight four(图3b)是直线上6个方块, 进攻方占据了中间4个方块位置, 外部2个方块位置为空；three(图3c或图3d)是直线上7个位置, 中间3个位置被占据, 其余4个位置为空, 或者直线上6个位置, 中央4个相连位置中3个位置被进攻方占据, 其余3个位置为空；broken three(图3e)是直线6个位置, 进攻方占据中央4个位置不相连的3个位置, 其他3个位置为空. 如果某方创造了一个four, 他无疑会在下一次行动中产生威胁. 因此必须被立即防御. 如果创造一个straight four, 防守方就太迟了, 因为进攻方在下次行动中有两个位置可以下子. 如果创造了一个three, 进攻方在下一回合将威胁产生一个straight four. 因此即使该威胁的深度为2, 它也必须立即被防御. 如果两边都能被扩展(图3c), 那样便有两种防御策略：都是与进攻方石子相邻. 如果只有一个扩展则3种防御策略可行(图3d). 并且对于broken three而言, 存在3种防御策略(图3e).

为了赢得游戏必须创建一个double treat(双重威胁). 威胁序列由威胁构成的一系列移动, 在双重威胁创造出来之前必须被创建. 一个导致双重威胁的威胁序列叫做胜利威胁序列. 序列中的每个威胁迫使防御方防御该威胁, 因此防御方的可能性是被限制的.

在图4中展示黑子可以通过一系列威胁序列获胜的位置, 该威胁序列仅仅由four组成. 因为一个four必须被立即防御, 因此白子移动是被强迫的.

在图5中展示了一个黑子可以通过一个完全由three组成的威胁序列获胜的例子. 在游戏中他可以创造2个four, 然而他还是不能避免地要输掉游戏. 我们标记出黑子方的威胁序列是独立白子方的防守策略的.

图3 威胁

图4 一个由four组成的威胁序列

图5 一个由three组成的威胁序列

一个专家棋手能够很快发现威胁序列可以被分为如下步骤:

a. 棋盘某个部分的形状看上去对进攻选手有利. 看是否有足够的石子能够合作可以使得能够搜索出一个威胁序列, 这依靠“感觉”, 是通过长期观察棋型训练出来的；

b. 威胁会被考虑, 尤其是与棋盘上面已经有的, 其他棋子相关的威胁. 对方的防御可以完全被忽略；

c. 一旦发现进攻方可以联合他的石子组成一个双重威胁, 将马上调查防守方如何防御这个可能获胜的威胁序列. 当对手有多于一种可能的防守策略时, 将检查是否该威胁序列在所有情况都能奏效, 并且调查对手能否创造一个或者多个four来中和进攻方；

d. 如果只有某些异样不能通过同样的威胁序列获胜, 检查剩余位置能否通过其他威胁序列获胜；

e. 在现实游戏中, 一个获胜的威胁序列通常由单方面组成, 与防守方的策略无关；

f. 特别的, 搜索空间通过进攻方第一次搜索显著改善. 当且仅当潜在的获胜威胁序列被发现, 防守方的影响才被调查. 这个分析过程由Sakata和Ikawa两位日本选手于1981年发表.

在没有获胜威胁序列的位置, 选手更愿意下的位置创造威胁的可能性更大, 或者不管任何时候防御被忽略, 被选择的移动将降低对手创造威胁的可能性. 选手评估局面可能性通常基于两方面: a)直接计算可能性; b)一个好的形状(石子能更好地合作的形状).

3.2 威胁空间搜索的过程

一个获胜的威胁序列由威胁组成. 因此我们关注威胁空间. 空间的大小通常由数百万位置组成. 因此重点放在: a)减小空间大小; b)在剩余空间尽可能地高效搜索.

一个重大的改善来自决定与威胁相关的防守. 五子棋专家通常选择和对手无关的策略. 与在防守策略中选择其一不同, 我们允许对手在同一时间执行所有可能的防守策略. 如果我们还能找到一个获胜威胁序列, 那么可以确定对手的移动无关紧要. 简要来说, 将搜索空间减少到只要搜索攻击移动(威胁), 它们之中任何一种存在相应的防守策略. 为了更加准确描述威胁空间搜索, 这里介绍6个概念.

a. 一个威胁中的gain方格是由进攻方下的方格；

b. 一个威胁中的cost方格是由防守方下的方格, 是为了应对威胁的；

c. 一个威胁中的rest方格是可能包含威胁的方格, 除掉gain方格；

d. 威胁独立于威胁, 当的某个rest方格是的gain方格；

e. 威胁的依赖树是有根和依赖结点组成, 每个结点的子结点是依赖于的威胁；

f. 两个依赖树相冲突, 如果在依赖树中存在威胁或者在依赖树中存在威胁, 在这种情况下:的gain方格是的cost方格, 或者相反, 或者的一个花费格也是的一个花费格.

威胁空间搜索可以由以下两个原则描述.

a. 威胁独立于威胁当且仅当不允许出现在威胁的搜索树中；

b. 在威胁空间搜索树中只包括进攻方的威胁, 在一个潜在的威胁序列被发现之后, 将调查该序列能否承受任何防御.

这两个原则描述了威胁空间搜索算法的核心和过程, 每次搜索一个分枝之前调用以上两个原则构成的威胁空间搜索, 将大幅减少无用计算. 这样实现程序的智能和效率都大大提高了, 归根结底因为这样将人的策略和思维方式加入到了程序中.

4 结语

虽然五子棋搜索是个不确定多项式问题, 不存在严格多项式复杂度算法, 但经过如此实现的程序, 在加入判重之后避免了重复搜索. 搜索的结点数目经过测试平均不足去掉判重的1/2, 而如果实现的时候引入部分棋谱, 当局面变成棋谱对应的经典局面之后便是索引的复杂度. 对于若干明显的局面引入特判(如自己一步能赢就必然下该步, 对手一步能赢必然要阻止等). 加入部分棋谱启发式估价过程每次搜索将分枝因子数目限制为至多10(事实上可以放宽数目限制, 这样实现的程序智能就更高了). 对于原来若有个结点, 分枝因子平均为200的情况下, 计算量最坏为(200). 而加入该优化之后计算量最坏为(10). 当然事实上由于alpha-beta剪枝该计算量不可能达到. 同时配合强力的威胁空间搜索将棋手下棋的很多“套路”公式化之后加入程序每次搜索提前判断, 大幅减少不用分枝搜索, 经过笔者测试最后对于每个局面搜索的分枝数平均不到2, 实际计算量约为(1.3), 实现的程序能在平均不到一秒的速度下做出高效反应.

[1] 刘汝佳, 黄亮. 算法艺术与信息学竞赛[M]. 北京: 清华大学出版社, 2004.

[2] Knuth D E, Moore R W. An Analysis of Alpha-Beta Pruning[J]. Artificial Intelligence, 1975, 6(11): 293-326.

[3] Donald Knuth, Ronald W Moore. Alpha-beta pruning. [EB/OL]. http://en.wikipedia.org/wiki/Alpha-beta_pruni- ng, 2002.

[4] Allis L V. Games and Artificial Intelligence[D]. Maast- richt Netherlands: Department of Computer Science, 1994.

[5] 郭瑞杰, 程学旗, 许洪波, 等. 一种基于动态平衡树的在线索引快速构建方法[J]. 计算机研究与发展, 2008, 45(10): 1769-1777.

[6] 张钹. 统计启发式搜索算法在函数优化中的应用[J]. 计算机学报, 1997, 20(8): 673-680.

An improved treat-space search algorithm

DU Si-han1, LI Ming2

(1. Software College, Hunan University, Changsha 410082,China; 2. Hunan University of Arts And Science, Changde 415000, China)

The problems was studied in the convetional minmax search and alpha-beta pruning, ranging from too much computation to too much useless computation. Then it was enhanced with judging duplicate search and heuristic. Only the best several strategies was selected to reduce the search work. Then further enhanced it with threat-space search, which was based on the strategies of professional players. After these work, making the computer’ thinking more like human’s can tremendousely reduce the complexity. In conclusion, after the test, the implemented program has high intelligence and give excellent respond to the players’ move quickly.

minmax search; alpha-beta pruning; judging duplicate search;heuristic; treat-space search

TP 301.6

A

1672-6146(2010)03-0073-04

10.3969/j.issn.1672-6146.2010.03.019

2010-05-08

杜思翰(1987-), 男, 研究方向为人工智能、字符学组合优化等.