开征物业税对土地利用效率的影响*——比较静态模型的理论分析与数值模拟

王智波

(华南师范大学经管学院,广东广州510006;华南师范大学华南市场经济研究中心,广东广州510006)

一、引 言

自2003年10月,党的十六届三中全会提出：“条件具备时对不动产开征统一规范的物业税”以来,物业税改革一直在积极稳妥地推进。本文正是在此背景下,致力于研究即将开征的物业税对土地利用效率的影响。当前,我国正处于城镇化、工业化快速发展阶段,土地资源紧张已经成为制约社会经济可持续发展的瓶颈。在这一严峻形势下,开征物业税对土地利用效率的作用方向和大小究竟怎样,已成为房地产税制改革中无法回避的重大理论与实践问题。

传统的物业税效率分析可归功于19世纪末的Cannan(1899)和Marshall(1890)。至今,这一分析方法仍然在教科书和政策建议分析中占有重要地位。传统分析的核心是将土地供给视为完全无弹性;将房屋建筑物(资本)供给看成完全有弹性。通过简单的图形分析可得到,物业税中对土地价值的征税部分,即所谓“地价税(land value taxation)”或“场所价值税(site value taxation)”是没有扭曲的,税负完全由土地所有者承担;对房屋建筑物价值征税部分,即所谓“建筑物价值税(structure value taxation)”是扭曲的,它将减少资本密度(资本—土地面积的比率,可以粗略地理解为容积率、建筑高度和建筑密度)。传统模型的关键假设——资本供给完全有弹性实质是指“建筑物具有完美可塑性”,然而,这一假设可能过于严苛了。

最近30年对物业税效率问题的研究进展沿三个方向展开：第一,引入一般均衡分析,从物业税转嫁的角度考察讨论物业税的效率问题。Mieszkowski(1972)从Harberge的静态一般均衡出发,提出建筑物价值税应被看作是对资本征税,它将减少资本市场上的均衡收益,因而该部分税负由所有的资本承担。Sullivan(1985)通过一个可计算的一般均衡(CGE)模型证明了Mieszkow ski的结论,他对以物业税代替土地税的情形进行了模拟,发现物业税将在开放城市中导致资本密度和城市人口的减少;而在封闭城市中将导致生产和就业转移到其他城市地区。Feldstein(1977)同样使用了一般均衡的方法,但从动态角度展开,所得结论也不尽相同,他否定了场所价值税是中性的传统观点。Feldstein通过考察一个简单的两阶段世代交叠模型,发现对土地征税将引导家庭持有更大数量的资本,从而削弱了资本净收益,因而,土地税也转嫁给了资本,并认为由此产生了无谓损失。

第二,引入空间因素分析,从空间均衡分析的角度研究物业税对土地利用的集约化水平的影响。这是一个最近发展起来的研究领域,主要文献有Brueckner和Kim(2003)、Yan Song和 Yves Zenou(2006)。Brueckner和Kim(2003)在Muth-Mills的空间一般均衡模型中引入物业税,他们发现物业税的作用是一方面会降低单位土地面积上的资本密度;另一方面会减少人均居住面积,从而物业税对城市蔓延与土地集约化使用的影响是不确定的。Yan Song和Yves Zenou(2006)则在居民的拟线性效用函数假设下简化并检验了Brueckner和Kim(2003)的一般性模型,他们得出了物业税有助于抑制城市蔓延的结论,不过,这一结论所依赖的拟线性偏好在Yan Song和 Yves Zenou的模型中要求居民的收入与其住房面积成反比,其一般性令人生疑。

第三,以建筑物的“耐用性”假设替代传统模型中的“完美可塑性”假设,来讨论土地税对土地利用效率的影响。目前,这一研究领域只关注房屋建筑物的生产供给方面,其主要方法是运用了动态资产定价理论将租金转为价值,将物业税视为是对价值而不是对租金征收,同时,假设土地开发后的资本密度不随时间变化,因而考察了物业税对耐用性建筑物,进而对土地开发行为的影响。这一研究方法依据其是否考虑土地开发的收益或成本具有不确定性,可归类为“确定型模型”和实物期权模型(见Turnbull(2005))。其中,确定性模型首先是由Shoup(1970)提出,他探讨了土地开发时机的选择,得出了土地的最佳开发时机是使土地价值增长率等于利率的结论。随后,Arnott和Lewis(1979)扩展了Shoup(1970)的分析,引入建筑资本密度作为土地开发的决策变量,使之成为物业税对土地利用效率研究的标准模型。实物期权模型由Capozza和Li(1994)引入,强调在不确定性及投资不可逆性的交互作用下,开发商具有延后投资的期权价值,因此,可借助期权定价模型考查在不确定性条件下物业税如何影响土地开发的资本密度与开发时机。

本文关注物业税效率问题的第三个研究方向——物业税是如何影响土地利用效率的。本文沿用了耐用性假设下的确定型土地开发模型,试图在符合我国国情的假设下,重建模型,克服现有文献中比较静态分析无法得出确定性结论的缺陷,并使用数值模拟的方法评估了开征物业税对我国土地利用效率的影响。我们相信,这一问题的厘清,对我国房地产税制改革有着重大的理论价值和现实价值。当然,本文不敢奢望能对相关问题给出完全正确的答案,只是抛砖引玉,希望通过讨论加深对问题的理解,使我国的房地产税制改革更加合理和有效。

二、理论模型

(一)无税条件下的土地一级市场模型

我们的分析框架是建立在由 Shoup(1970)提出,经 Arnott和 Lewis(1979),Turnbull(1988),Anderson(2005),Turnbull(2005),Arnott(2005)和Arnott、Petrova(2006)丰富和完善起来的房地产开发模型基础之上,并根据我国土地和房地产管理制度的特征与市场运行的实际情况,引入了(1)政府作为城市土地唯一的合法所有者,完全垄断土地一级市场;(2)通过征地拆迁,土地可以再开发;(3)物业税实行差别税率,对物业中的土地价值和建筑物价值适用不同税率,对征税前开发的存量房、农地和政府的土地储备免税;(4)政府规定土地出让后的开发时间。

我们模型的背景是,城市化进程带来了建筑用地需求的增长,对这一需求的满足依赖于城市空间扩张(征收农地)和城市土地再开发(旧城改造)。在城市化进程中,政府通过征地和拆迁取得土地,并作为唯一卖方在买方完全竞争的土地一级市场上出让土地;开发商竞价获得土地,并对拍得的土地进行开发。

在我们的模型中,房屋的租金r(t)为外生,随时间的变化而变化,而且与资本密度无关。单位土地面积上所能生产的房屋数量L(T,K)是由建筑资本密度决定。而单位土地的价值是由该单位土地的开发时机和资本密度共同决定。

基于我国房地产市场现实和数学处理上的便利性考虑,此做出如下假设：

(1)在政府征收土地前,土地上的物业可产生租金或农业租金,但土地在被政府征收以前,用途或资本密度不能改变;

(2)征地拆迁时,(a)政府按公平的价格补偿业主,业主的福利不因征地拆迁而变好或变坏;(b)旧建筑的拆除成本、土地平整成本为零;(c)征地拆迁的交易成本为零,即政府不但是公正的,而且是权威的,被拆迁户不存在讨价还价的策略问题。这三个假设意味着政府的征地拆迁成本为开发前物业或农业租金的现值;

(3)开发的物业不贬值,无折旧;

(4)土地使用权到期后的继期成本可以忽略;①

(5)开发商具有理性预期且为风险中性;

(6)土地市场上的完全竞争,保证了土地最有效率的利用,也保证了土地出让金等于土地价值,同时使得开发商只能获得正常风险报酬和为满足参与约束的无穷小的超额利润。

本文所使用的符号的含义如下：

t：时点(t=0表示今天);

T：开发时机,选择变量;

K：资本密度,表示单位土地上的非土地投入(资本)数量,选择变量;

r*(t)：在征地之前,由业主享有的单位土地上的物业的租金或农业租金;

Q(K)：房屋建筑物的生产函数;

r(t)：t时刻土地开发所形成物业的单位租金;

i：建筑资本的机会成本,是开发商承担房地产市场风险的必要收益率;

p：房屋建筑资本(非土地投入)的单位价格。

开发商的理性和竞争保证了其将选择最优的K和T,使土地资源的配置和利用达到帕累托有效。这时,开发后单位土地的租金现值与建设成本现值和征地拆迁成本之差实现最大化。t=0时,政府土地出让收入净值可表示为：

式(1)的一阶必要条件(FOC)是：

式(2)说明：当开发时间固定时,资本应该增加到额外一个单位资本所增加的租金,对开发时间折现后等于单位资本的价格p。式(3)说明：开发的最优时机是指推迟开发所节约的利益r*(T)+ipK,等于由于推迟开发所损失的物业租金r(T)Q(K)。

在K-T空间中,内部最优条件的一阶条件：LT与LK都有正斜率,并且LT斜率大于 LK的斜率,LT与 LK的交点决定了最优开发时机与优资本密度。Arnott和Lewis(1979)以及Arnott(2005)为内部最优的二阶充分条件的存在性和LT比LK比更加陡峭的原因提供了证明,本文不再赘述。

(二)几个与物业税税基有关的物业价值概念

我们假设市场竞争与开发商的理性保证土地开发全部出现在最优开发时机和最优资本密度上,以下不再强调,为简便起见,我们使用P(t)表示开发后物业价值来代替P(t;T,K)。

P(t)表示t时点上单位土地面积上所形成的物业产生的租金现值,也是由购房者支付的房价,此处t＞T表示开发后。

S(t)表示开发后t时点上剩余场所价值,它等于物业的价值减建筑成本,这里我们使用了假设(3)和假设(4),应有：

开发前,t＜T,t时点上的土地价值等于开发后物业的价值折现值减建筑成本的现值,它是政府的土地出让毛收入,可表示为S(T)e-i(T-t)。

L(t)表示开发前(t＜T)t时点上政府的土地出让净收入：

式(6)表明,政府获得了全部土地增值收益。这体现了19世纪亨利◦乔治所倡导的“Value capture——社会发展和公众活动所带来的土地增值,应由政府获得,以供全社会使用”精神和孙中山先生的“土地涨价归公”理想。

(三)引入物业税后的土地市场模型

1.这一部分使用的假设为：(1)物业税的征税对象是开发土地所形成的物业,存量物业和农地免税;(2)消费者是风险中性的,对支付时间和风险的改变无偏好,从而征税不改变消费者的最优选择,不影响房地产市场的需求;(3)征税对资本市场上的供求关系影响可以忽略,从而建筑资本的机会成本不变;(4)市场是理性的,不存在对房价和地价的高估和低估。

2.对物业税体系设计的解释。本文假设我国的物业税是不对存量房和农地征收,原因在于：首先,对存量房征税,不会对土地利用效率产生任何影响。因而,假设不对存量房征税不影响我们研究目标的实现,而且会使分析更为简单。其次,增加文章的新颖性,因为现有文献对这一物业税体系的土地利用效率问题没有系统研究过。最后,使本文假设的物业税体系更符合我国国情。

按税基的不同,我们模型中的物业税的税率设定为两种：一是以开发后土地价值为税基的剩余场所价值税税率,记为τS;二是以开发后建筑物价值为税基的建筑物税税率,记为τK。注意,除这两个税率外,文中的下标均表示偏导。

3.引入物业税之后的物业价值。这里,我们研究开征物业税以后的土地市场。

(1)征税后的物业价值也是购房者在购买环节所支付的金额。当 t＞T时,即有：

购买环节支付的减少,是由于保有环节需要付税,因而征税并不改变购房者支付的现值。

(2)征税后的剩余场所价值,t＞T时有：

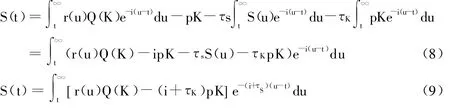
可以看出,对建筑物价值征税增加了非土地投入的资本成本,使之从原来的i增加到i+τK,而剩余场所价值税增加了开发后的折现率,使之从原来的i增加到i+τS。

(3)征税后政府出让土地的净收入为：

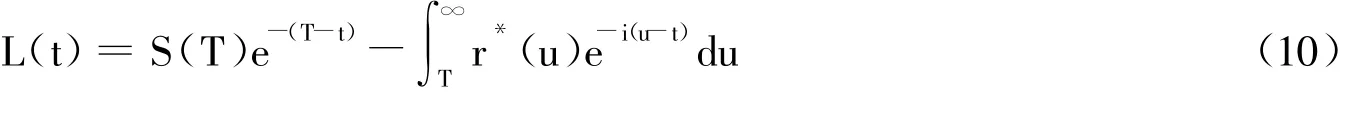
将式(9)代入式(10)并化简得：

一阶条件如下：

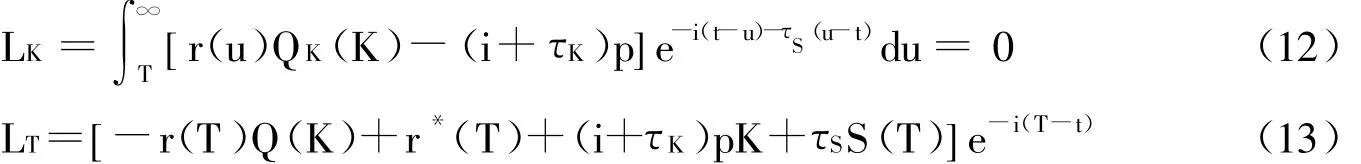
式(12)表示最优资本密度决策将最大化土地出让收入在t时刻的净现值。最优的K出现在,最后一单位的非土地投入贡献的租金r(u)QK(K)的现值等于使用者成本(i+τK)p的现值,所使用的折现率等于建筑资本机会成本i加上开发后剩余场所价值税率τS。式(13)表示最优开发时机出现在推迟开发一个时期的边际收益等于边际成本之时。边际收益等于推迟建设的节约收益,即建设成本pK乘以使用者资本成本i+τK,加对场所价值税的支出τSS(T),再加土地上原有物业的租金r*(T);边际成本等于放弃的租金收益r(T)Q(K)。

三、比较静态分析

(一)二阶导数符号分析

在讨论比较静态之前,检查二阶导数的符号会使后面的分析工作更为方便。为了简化计算,我们考察式(11)在 T时刻上的一阶条件：¯LK=LK(T),¯LT=LT(T),由式(12)和式(13)得：

由内部最优的二阶必要条件知,LKK≤0,LTT≤0,J=LTT LKK-L2TK≥0,但由于在物业生产函数中,资本的边际产量严格递减,所以LKK＜0;同时,由于¯LTT≤0,将得出rt(u)≥0;而 rt(u)=0表明租金房价增长率为零,这与我们所假设的城市化进程不符。因而有L TT＜0,L KK＜0,J=LTT LKK-L2TK＞0。

下面考虑资本密度与开发时间的交叉偏导的符号：

使用分部积分,改写LK为：

用式(16)替换上式的第一项得：

其中：rt(u)反映的是租金的时间变化率。由¯LTT＜0可知,rt(u)＞0;代入式(15)得¯LKT＞0。从上述推导中,我们得到命题1：当租金和房价时间增长率大于零时,随开发时间的递延,开发的资本密度将提高。这一命题与我国近几年随房价上涨而出现的新建住宅小区容积率增加和高楼林立的情况相符。

对式(14)和式(15)求物业税税率的导数得：

根据式(17)和式(18)知 ,¯LKτS和 ¯LKT符号相反 ,即 ¯LKτS＜0 。

我们把二阶导数符号总结如下：

表1 两阶导数的符号

(二)场所价值税和建筑物价值税对资本密度和开发时间的影响

对式(14)和式(15)分别求τK和τS的导数,使用克莱姆法则,可以解出通常意义上的比较静态分析：

根据表1所提供的信息,除非在非常偶然的情况下,上述任何一个比较静态分析式都不会等于零。我们得到命题2：无论是建筑物价值税τK,还是场所价值税τS都不是中性的。这一结论的引申意义在于,传统观点推崇备至的差别物业税的理论基础——地价税为中性的结论值得商榷。

然而,根据已知信息,我们还不能确定上述任一个比较静态分析式的符号。其原因在于(见图1)：建筑物价值税τK增加了非土地投入的资本机会成本,这一方面降低了资本密度,使曲线下移;另一方面却延后了开发时间,使曲线右移,而推后开发时间导致资本密度增加,因而总效应是增加资本密度还是减少资本密度取决于这两种方向相反的效应的大小。场所价值税τS对土地开发的作用与此相同,也是一方面降低资本密度,另一方面延后了开发时间。因而,要得出明确的比较静态分析结论需要更多的信息。

图1 建筑物价值税和场所价值税对最优资本密度和最优开发时间的影响

(三)政府规定了开发时间后的比较静态分析

在我国现实环境中,土地出让时间基本决定了土地开发时间。不过,也有报道称开发商囤积土地,这正是我们在模型中所预见的开发商将开发时间作为选择变量最大化土地开发利润。然而,这样的模式已经被打破,按2007年8月30日修订的《中华人民共和国城市房地产管理法》第二十六条的规定：“以出让方式取得土地使用权进行房地产开发的,必须按照土地使用权出让合同约定的土地用途、动工开发期限开发土地。超过出让合同约定的动工开发日期满一年未动工开发的,可以征收相当于土地使用权出让金百分之二十以下的土地闲置费;满二年未动工开发的,可以无偿收回土地使用权”。可见,目前在我国房地产开发管理制度中,时间选择被完全排除在开发决策之外,因而,开发时间不再成为一个选择变量,一阶条件式(13)不存在,土地价值由仅由资本密度决定,根据式(12),对τK和τS求导,我们的比较静态分析为：

我们很容易根据表1所提供的信息,判断比较静态分析的符号。我们得到命题3：政府规定了土地开发时间之后,开征物业税——无论建筑物价值税,还是土地价值税,或者它们的组合单一税率物业税都将减少资本密度,降低土地利用效率水平。

这里,我们进一步说明资本密度的减少不仅会导致量的变化——容积率的降低,而且还会带来质的变化——房屋的质量的下降,要知道房屋的质量、功能、品质和外观等都与资本投入数量有关。

四、数值示例

比较静态分析揭示了开征物业税将对土地利用效率产生负面的影响,但却不能得出这种影响的大小,为了直观说明资本密度降低的程度,这里对开征物业税对土地利用效率的影响进行数值模拟。

为简化计算,我们假设物业租金增长率恒为η,且η＞0,并假设零时刻政府宣布征税。上标b表示征税前,上标a表示征税后,那么,式(2)化简为：

式(12)化简为：

假设开征物业税不影响非土地投入的价格p,同时假设物业税实行单一税率,τK=τS=τ。由式(19)和式(20)可得：

设土地开发满足规模报酬不变的Cobb-Douglas生产函数,则单位面积土地开发生产函数为Q(K)=c0 Kc1,其中：c0是转移参数,c1是Cobb-Douglas函数的资本产出弹性或者说资本份额参数,QK=c0c1 Kc1-1。

设c0=1,Kb=Qb=1。这可以简单理解为在开征物业税之前,资本密度为1,此时容积率等于1。②设不动产投资的资本机会成本i=0.06,房价增长率η=0.03,在这一假设下租金房价比率为3%,与我国的城市房地产的租金收益率相近。我们选择在物业税税率分别为τ=0.005、0.01、0.02、0.03,资本(非土地投入)在物业价值中的比重分别为 c1=0.3、0.4、0.5、0.6、0.7的不同情况下,模拟物业税对资本密度的影响,数值模拟结果见表2。

数值模拟的结果与比较静态分析的结论是一致的,开征物业税导致资本密度下降。同时,数值模拟进一步提示我们,征税所引起的资本密度的降幅是惊人的,其变化有两个特征：一是在相同税率下,征税造成的资本密度降幅随资本在物业价值中所占份额的增加而变大;二是在相同资本份额水平下,征税造成的资本密度降幅随物业税税率的提高而变大。

表2 租金收益率为3%,土地-资本替代弹性等于1时,开征物业税对资本密度的影响

五、结语及讨论

在本文中,我们构建了符合我国房地产开发市场制度特征的“物业税—土地开发”模型,通过比较静态分析和数值模拟,发现土地价值税和建筑物价值税都是扭曲的;并且在限制开发商的开发时间情况下,证明了开征物业税,无论是按土地价值征税,还是按建筑物价值征税,或者是对其组合形成的房地产价值征税,都将减少资本密度,降低土地利用效率。本文的发现对于我国在人多地少、土地资源稀缺、大量农村人口亟须转移、城镇化和工业化进程加速条件下推进房地产税费制度改革有着重要的理论意义与现实意义。

本文在论证过程中,为简化计算,使用了一些特殊假设,如(1)建筑物具有无限耐用性,这使我们无须在物业建成后计提折旧;(2)土地使用权续期成本可忽略。当然,放弃这些假设,并不会实质性改变我们的结论,只是计算更为复杂。

虽然,本文对物业税对土地利用效率的影响提供了一个相当合理而且稳健的分析,但是仍然存在一些问题有待未来更深入的研究予以解决。

1.物业税对土地集约利用水平的影响。本文关注的是在局部均衡中土地的利用效率问题,假设了开征物业税不改变需求因素。但是,在一般均衡中,房屋供给的减少将影响房地产市场价格,价格的改变会影响购房者的最优选择。因而,物业税对集约利用土地存在两方面的影响：一是降低资本密度,减少单位土地面积上的房地产供给;另一方面,在降低居民效用水平的条件下,减少了居民对房屋的需求。在这两方面的影响中,具体哪一种影响占主导地位是我国城市土地开发中需要考虑的一个问题,对此更深入的分析需要进一步通过空间一般均衡模型来完成。

2.对存量房征税的效率问题。因为在房屋耐用性假设下,对存量房征物业税不会改变土地利用效率,因而,本文没有讨论对存量房征税的效率问题。然而,对存量房征物业税将迫使一部分家庭调整住房,缩小面积,从而释出一部分存量房。虽然,家庭的避税行为不改变建筑的资本密度,但将提高土地集约利用效率。当然,对存量房征税还将产生极为敏感的公平问题。

*(1)本文曾在中国房地产学术研讨会暨高等院校房地产学者联谊会2009年年会上报告,并获得优秀论文奖,感谢与会代表的批评与建议。(2)本文为广东省高校学科建设创新团队重大项目(C10082)和广东高校优秀青年创新人才培养项目(开征物业税对城镇土地利用效率与集约化水平的影响)的阶段性成果。

注释：

①在信息不对称条件下,购房者没有估计到在购房后的保有环节,政府会再对他的房屋征收物业税,因而其购房时的出价中没有扣除物业税现值;在信息对称(宣布征税)条件下,这一情况不会发生。土地出让金、营业税、契税、土地增值税、对房屋交易资本利得所征收的个人所得税、房地产开发企业所缴纳的企业所得税等与房地产价格有关的税费将由于征税所导致的房价降低(税收资本化)而降低。这说明,在开征物业税之前,与房地产价格有关的税费中已经包含了物业税。因此,对存量房再征物业税,存在重复征税的问题。

②据报道,2002年我国城市的平均容积率为0.33,我国香港的容积率是2.0。资料来源：樊志全：我国城市人均用地面积超国标1/3形势严峻,http：//finance.people.com.cn/GB/1037/4473961.html。

[1]王智波.房地产税制中的国际惯例与物业税的经济学分析[J].经济科学,2008,(5).[2]Mieszkowski P.The property tax：An excise tax or a profit tax?[J].Journal of Public Economics,1972,1：73-96.

[3]Sullivan,Arthur M.The general-equilibrium effects of the residential property tax：Incidenceand excess burden[J].Journal of Urban Economics,Elsevier,1985,18(2)：235-250.

[4]Feldstein,Martin S.The surprising incidenceof a tax on pure rent：A new answer to an old question[J].Journal of Political Economy,University of Chicago Press,1997,85(2)：349-60.

[5]Brueckner J K,Kim H.Urban sprawl and the property tax[J].International Tax and Public Finance,2003,(1)：5-23

[6]Song,Yan&Zenou,Yves.Property tax and urban sprawl：Theory and implications for US cities[J].Journal of Urban Economics,Elsevier,2006,60(3)：519-534.

[7]Turnbull,Geoffrey K.The investment incentive effects of land use regulations[J].Journal of Real Estate Finance and Economics,2005,31(4)：357-396.

[8]Arnott R,Lewis F.Thetransition of land tourban use[J].Journal of Political Economy,1979,87：161-169.

[9]Capozza D R,Y Li.Intensity and timing of investment：The case of land[J].American Economic Review 1994,84：889-904.

[10]Turnbull,Geoffrey K.Property taxes and the transition of land to urban use[J].Journal of Real Estate Finance and Economics,1988,1：393-403.

[11]Anderson,John E.Taxes and fees as forms of land use regulation[J].Journal of Real Estate Finance and Economics,2005,31(4)：413-427.

[12]Arnott R.Neutral property taxation[J].Journal of Public Economic Theory,2005,7：27-50.

[13]Arnott R,Petrova P.The property tax as a tax on value：Deadweight loss[J].International Tax and Public Finance,2006,13：241-266.