弯形渠道水流偏斜问题探讨

郭晓宇，段喜明

（山西农业大学林学院，山西太谷030801）

近年来，水资源的开发利用越来越受到人们的重视，为实现水资源优化配置，各种水利工程设施也越来越得到广泛的应用[1]，在各种水利工程设施中，弯形渠道是水利工程设计中遇到最多的引水设施，关于弯形渠道水流运动特点以及冲刷机理一直是河流动力学中的重点课题。当水流流经转弯渠道时，随弯道曲率半径的减小水流偏斜将更加严重[2]。这是由于当水流通过弯道时，液体质点除受重力作用外，同时还受离心惯性力的作用，曲线运动的弯道水流在重力与离心力作用下将产生特有的运动特性，主要表现为水面纵横比降、横向环流、纵向垂线平均流速重分布等[3]，由于几个方向的流动交织在一起，水流呈螺旋状的路线前进。由于水流流动复杂，目前关于转弯水流没有成熟的计算公式，一般弯形渠道设计都是按照直渠水流流态进行设计，再进行适当系数修正，本试验结果可为弯形渠道设计提供参考。

1 试验概况

本试验弯形渠道位于左岸，进口底高程923.28m，总长113m。包括进口控制段、缓坡段、陡槽段、尾水渠。设计最大泄量188m3/s。渠道左边墙内侧边坡为1∶0.4，右边墙内侧为直墙。缓坡段为0～20m，底纵坡i=1/500，底宽14m。陡坡段为20～105m，底纵坡i=1/4，底宽14m。其中，20～28m为直线段，28～98m为弯道陡坡段，弯道半径为92m，左边墙内侧边坡为1∶0.3，右边墙内侧为直墙。直线陡坡段为98～105m，左侧内边墙由1∶0.4渐变为直墙，右侧内边墙为直墙。105～113m为反弧与挑流消能段，反弧半径为12m，挑流采用连续重力式鼻坎。

2 试验结果

2.1 渠道内水流流态

在设计流量下渠道主要部位底部流速如表1所示。

明渠水流流态的判别一般用佛汝德数来判别，依据佛汝德数计算公式Fr=，得到在设计流量下，渠道各主要部位的Fr数（表2）。

表2 设计流量下渠道各主要断面Fr数

根据佛汝德数判别明渠水流流态的指标：当Fr＜1时，水流为缓流；当Fr=1时，水流为临界流；当Fr＞1时，水流为急流[5]。结合表2所测数据可知，渠道在设计流量下，弯道及挑流段水流流态为急流。

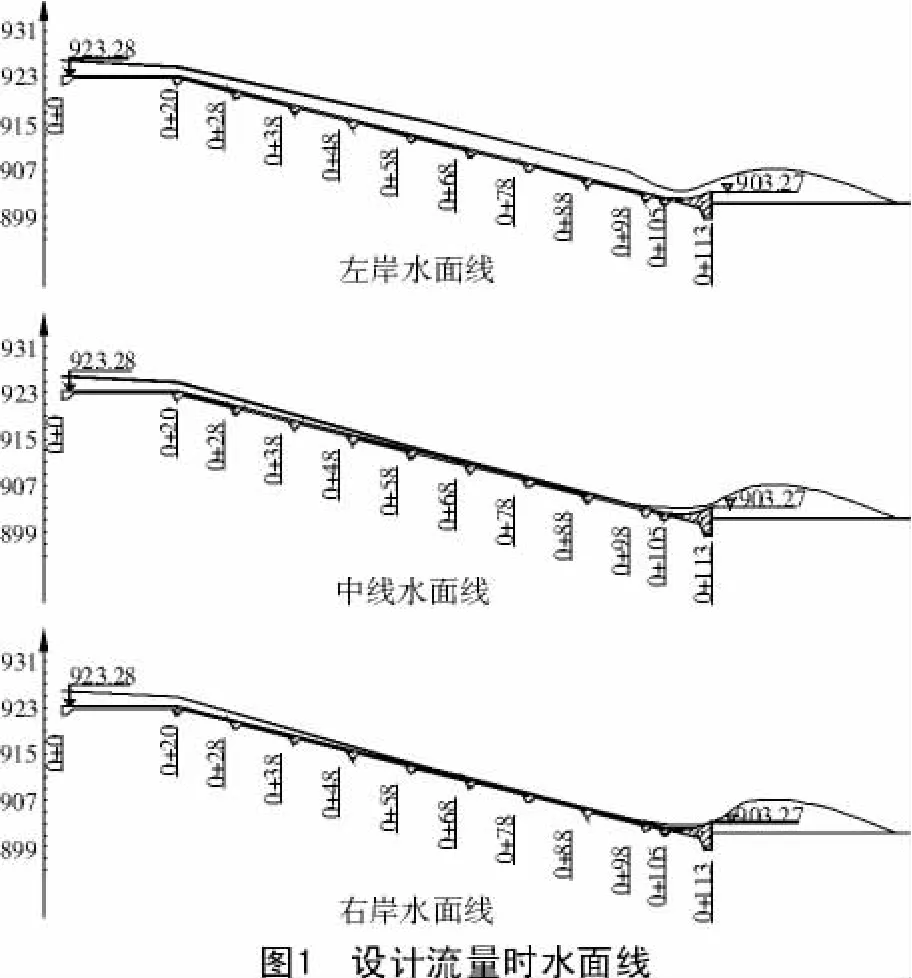
2.2 水面线图

在设计流量下的水面线如图1所示。

3 调整方案

3.1 调整方案Ⅰ

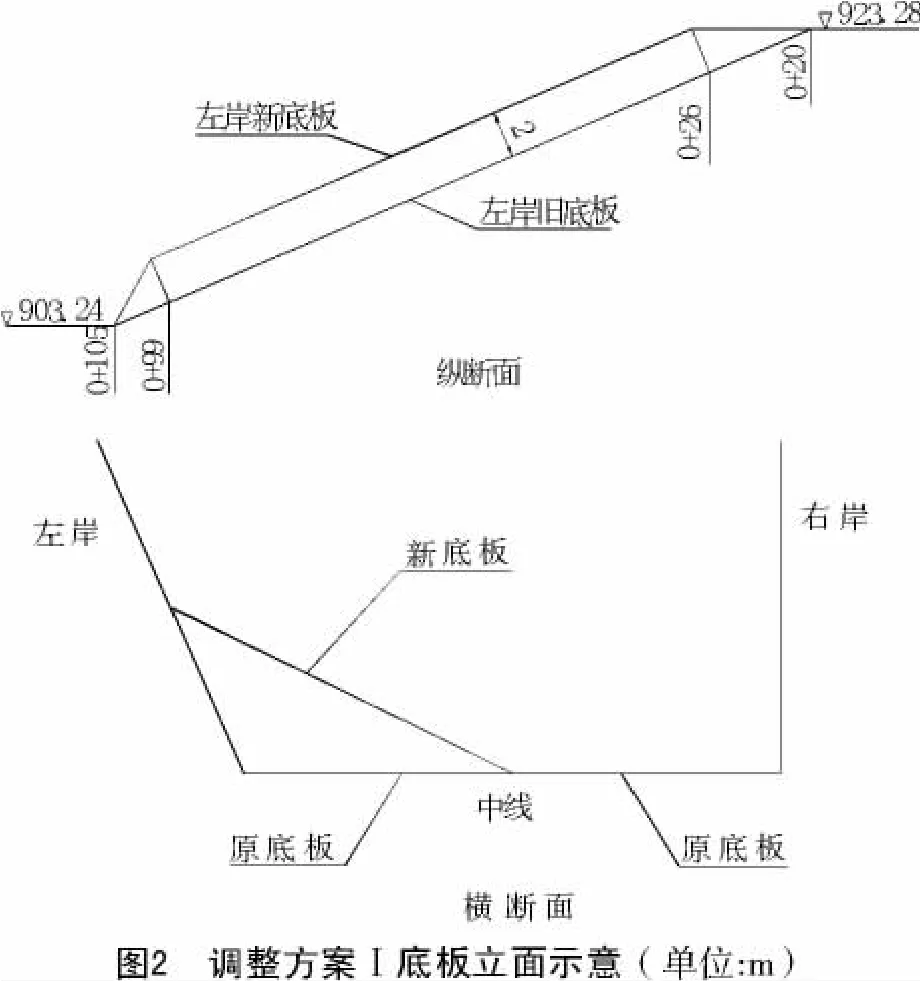
3.1.1 弯道底板布置 调整方案I是在原设计方案的基础上，把设计方案的斜面左边墙底板从桩号0+26到桩号0+99全部加高2m（图2）。

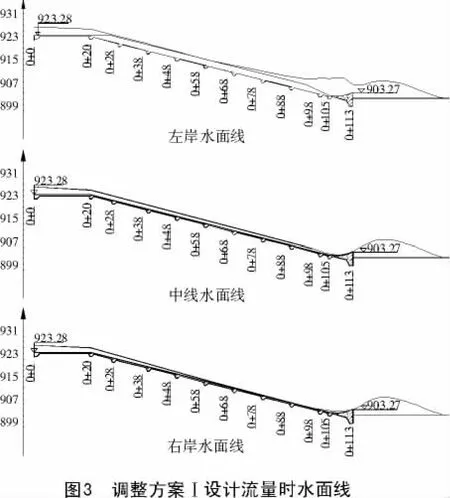
3.1.2 调整方案Ⅰ水面线图 调整方案Ⅰ在设计工况下的水面线如图3所示。

3.2 调整方案Ⅱ

3.2.1 底板和左岸侧墙布置 调整方案II是在调整方案Ⅰ的基础上，除左岸底板抬高外，还将左侧部分边墙由原设计的曲线变成直线（图4）。

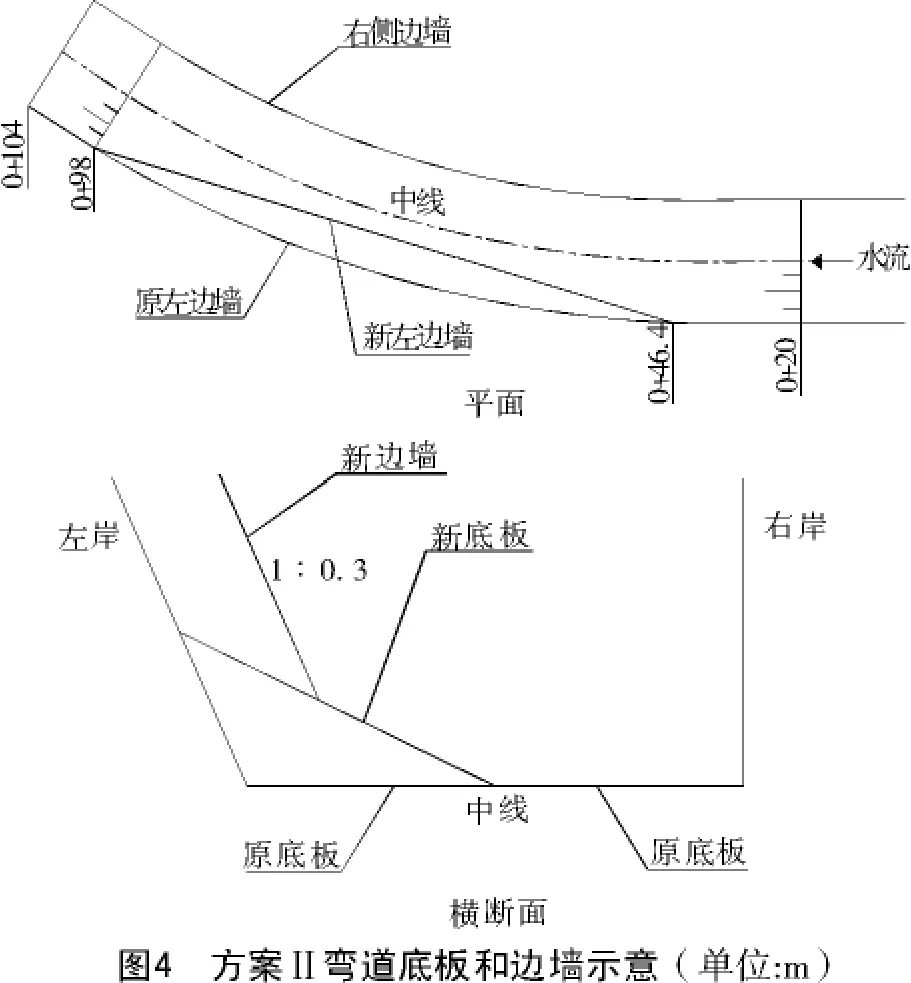
图4中底板同调整方案Ⅰ（图2），然后在抬高底板之处，从桩号0+47到0+99将左岸边墙取直，边墙仍按1∶0.3作成斜墙。

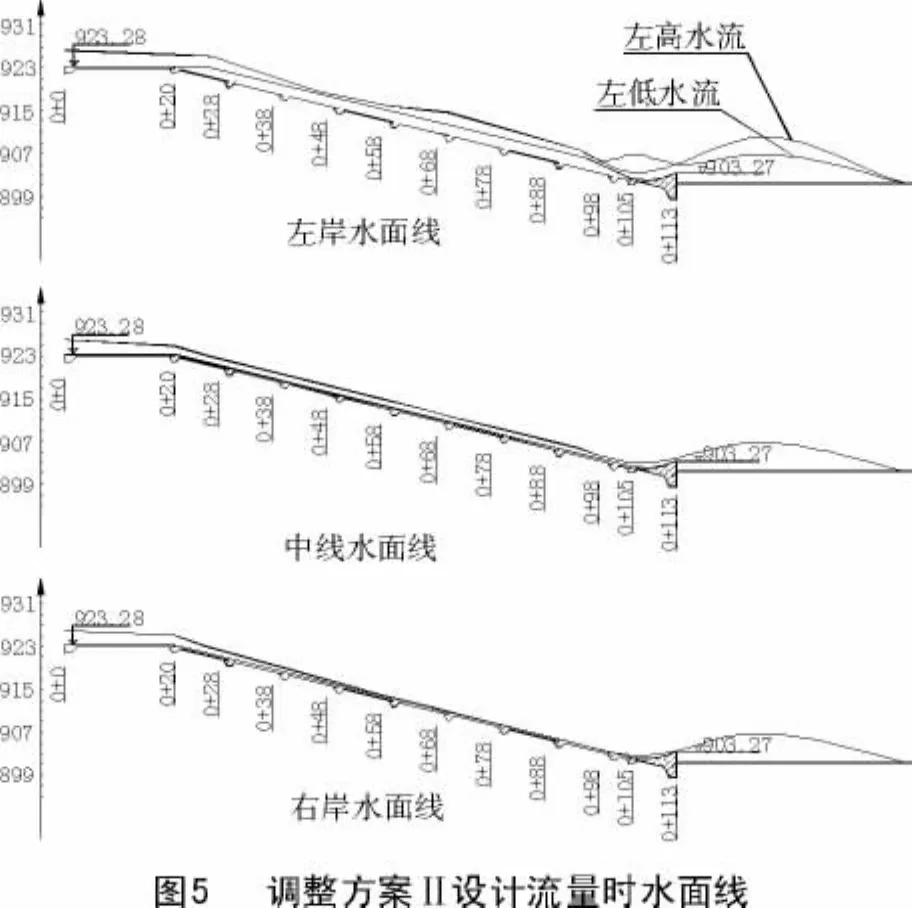
3.2.2 水面线图 调整方案Ⅱ设计流量下的水面线如图5所示。

3.2.3 调整方案Ⅱ流速分布 调整方案Ⅱ流速分布如表3所示。

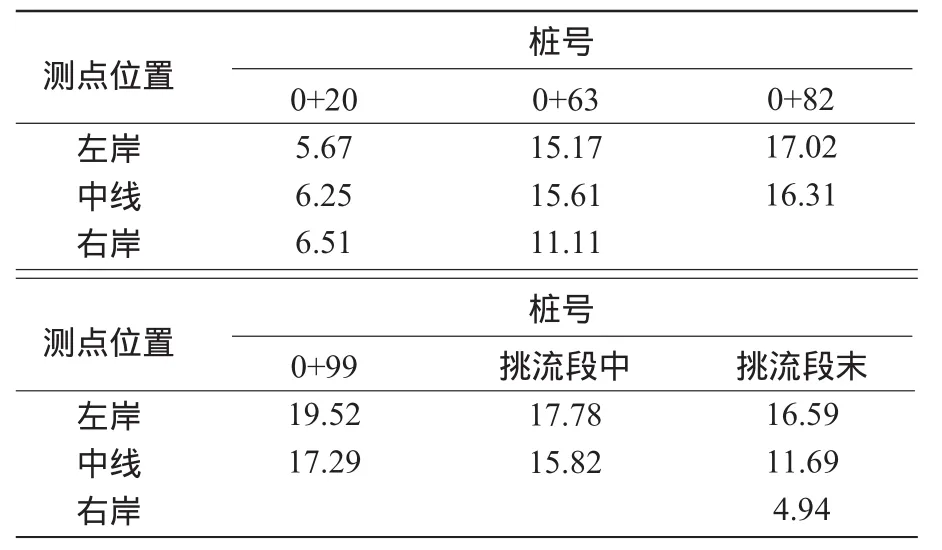
表3 调整方案Ⅱ设计流量下各测量断面流速 m/s

4 结论与讨论

通过以上3种试验方案的水面线示意图比较可以看出，为了调整弯道水流偏斜而对左岸底板作出的修改，调整方案Ⅱ对水流偏斜的调整效果较好，并且左岸边墙从桩号0+47到0+99将取直后节约工程量，减少了工程投资。经模型试验，在设计流量下，弯道及挑流段中水流为急流，符合实际水流流态[3]。

水在流动的时候，受边界条件的影响很大。边界条件的微小变化，就可能引起水流形态的巨大变化。有弯形渠道必定会出现弯道水流。经模型试验所得结果可知，其凹凸两岸水深超高过大，在左岸靠近挑流段附近区域甚至出现无水流情况。左岸、中线、右岸水面线相差很大，水流不稳定，为此对原设计方案进行了调整。最后得出调整方案Ⅱ相对较好，其在保证过流能力、流态等相同的情况下，能较好地解决弯道水流偏斜的问题。

明渠弯道水流是工程实际中经常碰到的一种水流形式。确定渠道设计方案时，应对水流特性、工程量和工程造价等进行优化选择，在保证安全和合理的水流衔接的前提下，应力求减少工程量和降低工程造价。

［1］ 赵学华.晋中市水资源优化配置研究 [J].山西农业科学，2007，35（7）：87-89.

［2］ 吴持恭.水力学[M].北京：高等教育出版社，1998.

［3］ 高伟，杨中华.弯道水流特性和数值模拟方法研究进展[J].水电能源科学，2009，27（1）：112-115.

［4］ 李炜.水力计算手册[M].北京：中国水利水电出版社，2006.

［5］ 武汉水利电力学院，华东水利学院.水力学[M].北京：人民教育出版社，1981.