反舰导弹规避编队雷达威胁源的航路规划*

顾鲁青 孙 翱 顾 杰

(91550部队指控中心 大连 116023)

1 引言

当今世界最先进的水面舰船,装备了以“宙斯盾”为代表的防空系统,对抗反舰导弹的能力很强。舰群编队警戒雷达,可远距离发现来袭的导弹,充足的预警时间,快速和强大的电子和火力反应能力,很可能挫败导弹的攻击。用反舰巡航导弹对付此类装备的舰群编队,没有超常对策或战、技术难以奏效。

攻击防御能力强的对象,反舰导弹受到的最主要威胁是被对方感知装备过早发现,或其生存力很大程度上依赖于巡航段的隐蔽性。而采用掠海超低空飞行、低雷达反射截面等对抗策略,既有某些优势,也存在局限性。如何扬长避短、发挥导弹武器系统的优势,有效规避编队雷达威胁源的探测,是巡航段保持隐蔽性的关键。而正因为如此,反舰导弹才需要以低探测概率为优化目标的航路规划。

2 攻防对策浅析

反舰导弹与舰艇编队的对抗,仅在中小规模的局部战争中出现。理论研究的素材多源于试验及少数战例。目前主导该武器系统发展方向的主要理念体现在攻防双方的对策上。

1)导弹方对策。针对编队的防御,反舰导弹采取的主要对策,体现在追求和评价其性能指标上。优异性能常可概括为“三超”:超视距发射、超低空飞行和超音速突防。

2)编队方对策。针对反舰导弹威胁,舰艇编队发展了网络化多感知系统、空中化早预警系统、电子对抗系统和远中近程的区域防空系统。在“宙斯盾”基础上发展的CEC交战系统,或是编队对策的代表作。

2.1 超低空对策分析

反舰巡航导弹为数不多可选的、和最重要的规避雷达威胁源的对策是掠海超低空飞行。

2.1.1 视距公式

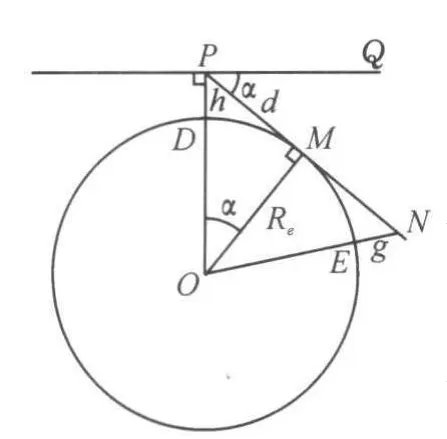
图1 观测点位置与通视关系的几何图

视距为可直视或雷达直波可达的距离。因球面的曲率,大地表面两点是否通视取决于两点间的距离及各自的高度。如图1所示,假设雷达辐射源在P点,距海平面高度 DP为h。地球大圆弧DM的长度等于地球平均半径Re与a(弧度)的乘积。即有

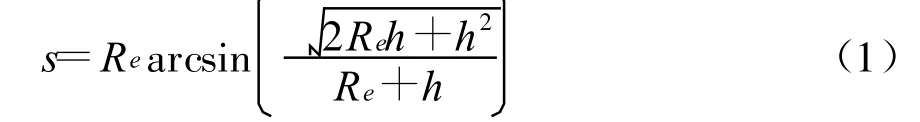
s为大圆弧DM 的长度,等于在高度h的P点观察远处海面能见的最远距离。

按WGS-84标准的地球形状数据,地球平均半径Re为6371001m,和 h=5～90m 代入式(1)计算,可得表1。

表1 天线高度与最大测距关系

即雷达天线高度如果按20m高算,对海面的最大通视距离约为16km。

P点与M点以远的目标是否通视取决于后者的高度。实际导弹飞行至少还需1～5m的高度,故暴露的距离还更远些。如图1所示,设从N点向O点做垂线交球面于E点,大圆弧DE的长度可由下式计算。

按式(3),取高度h=20m和g=5m计算,距离d约为27km。由此可见超低空隐蔽所能达到的极限。

2.1.2 上半球空间

按图1所示,以PN为母线绕PO旋转形成的曲面是一个锥面。再以P为球心,r为半径做一球面;则锥面以上与球面合围的空间,即所谓的上半球空间。若生成球面的半径r代表P点雷达的最大探测距离,则此上半球空间即为雷达的可探测空域。

在通视空间内,可探测仅在最大作用距离(阈值)为半径的范围内有效。在靠近边缘区域(目标的雷达信号从时隐时现到稳定跟踪的过度段),可用模糊度或发现概率描述。

2.2 距离优势

反舰导弹的优势在于:1)掌握进攻的主动权;2)编队强得多的机动能力。

因编队处于防御的被动地位,不得不依赖警戒雷达不停的工作。若导弹不主动发出雷达波,则编队必须靠雷达发出和接收目标回波来获取空中威胁信息。因此难以避免为导弹的雷达侦察提供机会。由于雷达侦察的距离优势,反舰导弹可在威胁源最大探测距离以外感知它的辐射。充分利用此优势夺取电磁对抗的主动权,对规避雷达威胁有很重要的意义。

3 航路及战术

导弹于巡航段须飞超低空而使垂直方向限制在狭窄的通道内。因此,它不得不,且很有必要在水平方向上寻求发挥机动能力的优势。水平机动反映为飞行路径,它取决于航路规划。

3.1 航路威胁

航路规划在技术层面上,其首要目标是确保导弹到达自控终点,以便在该点使弹上末制导系统捕获目标[2]。然而在对抗条件下,航路若不考虑威胁源的分布,则易遭侦测和拦截,达成战术目标的机会势必大为减少。

舰船作为反导对抗系统的载体,对反舰导弹既是威胁源,也可能是已选中要攻击的目标。航路规划的任务是,规避非攻击目标的威胁源,而尽可能接近和突防要攻击的目标。威胁源除非是既定的攻击目标,否则航路应与它保持尽可能远一点的距离。然而,这还受编队单元密集与离散程度的制约。

3.2 战术目标

如果导弹要攻击编队中被护航的核心舰只,必须穿过其外围护航舰只组成的防御圈。而编队为保持无缝隙和足够的防御纵深,核心舰、护航舰彼此间距均保持在一定范围。比如下限为近防炮的射程之外,上限为各自舰空导弹武器拦截半径之交的范围内。对于此类防御阵式,除集中火力摧毁一艘护航舰打开缺口外,很难直接攻击核心舰。

但战时,编队保持阵形并非毫无难度。如战损、补给,或为躲避侦察、水雷和潜艇伏击等,不得不绕行或变换队形,或受到诸如或电磁压制、电磁脉冲武器或反辐射导弹攻击至雷达失效等情形,均可使防御圈出现缺口,从而为对方攻击提供可乘之机。

反舰导弹武器系统,如果能够发现、利用甚至制造类似漏洞,即让导弹飞抵既定攻击目标的突防位置之前,利用上述漏洞选择航路,则实现战术目标的机会将大为增加。

4 威胁源模型

建立威胁源的适当模型是处理飞行威胁所必要的。在有关威胁源模型方面,注意到Voronoi图等[3～6]的前期研究;受数字高程模型(DEM)在陆上巡航导弹成功应用的启发,试图将其引入反舰导弹的航路规划。

4.1 威胁强度

导弹受到的主要威胁是被编队侦测传感器感知和对空拦截火力摧毁。由威胁源的这两种属性差异,不妨称前者为软威胁,后者为硬威胁。

据雷达方程[1],在通视的空域内,反射式雷达能否发现目标取决于回波的能量(信噪比),它和距离以及目标的RCS等因素有关。

式中,Pt为雷达发射机的峰值功率;Gt为雷达发射天线的增益;Gr为雷达接收天线的增益;σ为目标雷达反射截面积;λ为波长;L为总损耗系数;k为玻耳兹曼常数;Te为接收系统总噪声温度;Δf为信号带宽。

因威胁的非均匀分布,所处的位置不同,则所受威胁的强度也不同。为便于计算机处理,需要对威胁强度加以量化。下面以软威胁为例,讨论建立威胁强度空间的模型。

设编队有n个威胁源,空间某点与n个威胁源的距离为d1,d2,…,dn。据式(4)可知,其它因素不变的前提下,该点至各威胁源的反射回波信噪比为:

式中i=1,2,…,n;C0为由式(4)导出的等效常量;di为点与第i个威胁源的矢径。

根据理论推导和实验,可确定信噪比的两个值,下限和上限。设发现(如 0db)为下限S NRa;稳定跟踪(如10db)为上限SNRb。信噪比若不大于下限,定义为发现概率为0;若大于上限,定义为发现概率为1即有:P(snri≤SNRa)=0和 P(snri＞SNRb)=1信噪比snri介于下限和上限之间,发现概率Pi(snri)取0～1之间的某一值,应用可建立两者函数关系表格或近似多项式。

按上述定义,空间任一点所受威胁的强度可用被发现概率来描述。

以上是导弹所受软威胁强度的描述。

与此相仿,空间某点可按各威胁源的对空火力模型,描述被拦截摧毁威胁的强度。

在按PΣ的地理分布做航路规划之前,先回顾一下数字高程模型(DEM)的基本概念。

4.2 数字高程模型

数字高程模型(DEM)简介,将局部地区用与经度线平行的等间距的纵线和与纬度线平行的等间距的横线划分成格网,以每个格中心(最大或平均)的海拔高度代表该格网单元的高程。如以n+1条纵线和m+1条横线,可将一块地区划分为m*n个格网单元。以h(i,j)(i=1,2,…,m;j=1,2,…,n)表示第i行,第j列格网单元的高程。如此,该地区的地形—高程可用一m*n的实数h(i,j)矩阵描述。

数字高程模型应用于陆上超低空飞行器的航路规划,它的“高程”是反映真实地形障碍物的海拔高度。

对反舰导弹而言,威胁源具有障碍物的属性。空间某点所受威胁强度可用被发现概率描述。因此,由威胁源生成的威胁空间强度的地理分布可以这样描述:第i行,第j列格网单元,可用在该单元被发现概率PΣ(i,j)表示,或可称之为该格网单元的伪高程。

将导弹航路规划区域按上述方法划分成格网,输入威胁源的坐标后,即可计算各单元的伪高程。

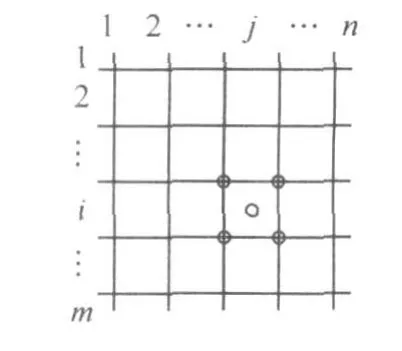
图2 单元格(i,j)钻石矩形取值示意图

计算时,如果一个单元矩形内仅取中心一点可能偏差明显,可采用“钻石-矩形(Diamond-Square)”的方法取样。即在矩形的四个角各取一值,与中心点的值加权平均。如图2所示。

用PΣ(i,j)代替DEM 中的高程,即得到反映威胁分布的平面图。如果对格网图各个单元矩形按数值以不同灰度等级着色,则可直观的显示危胁强度的二维分布。

为区别传统的DEM,以上定义的数字高程模型,不妨称为广义数字高程模型。

4.3 计算步骤

计算单元伪高程主要流程:

第一步,按式(3)判与第i个威胁源是否通视,不通视,则 Pi=0;否则到第二步。

第二步,按式(4)导出式(5)计算snri,如果小于SNRa,Pi=0,如果大于 SNRb,Pi=1;否则到第三步。

第三步,按snri在(0,1)对应函数关系(表格)求得 Pi值。

第四步,第i个威胁源是否为最后一个?否则换下个威胁源,回到第一步;是到第五步。

第五步,按式(6)计算 PΣ。

计算时,PΣ(i,j)的代替值,最好是转换为整数的变换值,如2n-1*PΣ(i,j),(n为整型变量的字长)。因计算机整数运算速度远高于浮点数运算;对于值域为[0,1]的数,浮点型变量浪费字长,且转换几无精度损失。

4.4 广义DEM制约因素

广义DEM的高度动态性。地形在军事活动期间内基本保持不变,而舰艇编队位置和队形是变化的。高度动态性要求C4ISR系统能提供敌我态势最新数据支持。因此,其应用有赖于强大的空中传感器和数据链,亦即装备具有高度的战场态势信息获取能力。

编队火力威胁模型较复杂。一方面导弹所受威胁强度是它与威胁源距离的函数;另一方面还与其运动速度有关。特别是在临界区:如仅在边缘擦过,舰对空火力如导弹(激光例外)拦截难奏效。或硬威胁空间仍可再细分为可逃脱区和不可逃脱区。因此,建立较准确的硬威胁模型有些难度。

情报收集能力也将在很大程度上制约该技术的应用。广泛收集包括潜在作战对手在内的世界各国海军装备的情报,建立完备的外军舰船数据库,则是应用广义DEM的信息基础。如宙斯盾系统是重要的参考。诸如相控阵雷达“SPY-1D”的性能 ,“标准 2\3”导弹、“海麻雀” 、“拉姆”和“密集阵”等武器装备的性能,可构成相应的广义DEM的标准数据。而储备数据的真实有效程度取决于情报收集与侦察能力。

5 基于广义DEM的航路规划

建立雷达威胁源的广义DEM模型,即具备了采用格网导航(Grid navigation)技术作航路规划的基础。在描述雷达探测威胁强度二维分布的格网上,可找出受威胁最小的路径,即做出以最小探测概率为优化目标的航路规划。

路径规划可用的方法,如Dijkstra[7]、Floyed[7]、A*搜索算法[3]、蚁群算法[4]、粒子群优化[5]和遗传算法[6]等。求解计算可选择效率高的算法。

威胁源转换为等效障碍物的“高程”后,各算法本身并不介意模型中数据的确切含义,均作为度量障碍的数据处理。与传统的航路规划(如DEM的)一样,将求所受威胁最小的路径问题,转化为图论的求加权最短路径问题求解。

航路规划前后须对数据做必要的预处理和后处理。预处理如,对图中伪高程全集作数理统计获取数据分布信息。当图中的极差过小,即对比度过低,可用相对性原理解决。如以平均值为基准比较大小。后处理如,初步规划出的航路可能存在不可飞的锐角,局部须按飞控参数将锐角钝化等。

导弹的雷达反射截面有方向性。假如已知导弹雷达反射截面的方向图,则在按式(4)计算时,σ值的大小须关联导弹姿态。若能使其最小的一面朝向威胁源,则可减少被发现概率。

总之,航路规划,技术层面是涉及导弹和威胁源两者位置、速度及姿态的多变量的最优控制问题;战术层面涉及军事运筹的问题;其高度复杂性不容低估。而广义DEM航路规划,着重解决导弹位置与威胁空间的关系。

6 结语

探寻提高反舰导弹生存力的航路规划技术,推广DEM的基本方法,试图建立将威胁源转换成等效障碍的模型,再与常规路径规划方法嫁接,以找出受威胁最小的飞行航路。

信息化条件下的战争,敌对双方武器的对抗是系统与系统之间的较量。用反舰导弹攻击敌舰群编队,体现的是导弹武器系统与反导防御体系之间的对抗。单项武器仅是陆海空天一体化作战体系的组成部分,它必须和整个大系统保持紧密有机的联系,才可充分发挥其作战效能。而联系的核心要素是信息,亦即获取、处理、传送和利用信息的能力。因此,说现代信息技术是传统武器系统效能的倍增器,其意义也在于此。

航路规划很大程度上体现了先进信息技术在导弹武器系统中的运用,它加强了导弹对战场态势信息的随机应变能力,因此是武器信息化、智能化水平的一个明显标志。作为反舰导弹武器系统重要的战、技术指标,优异的航路规划能力是战术应用软件极力追求的设计目标。即使更多从战术层面考虑,航路规划也须强有力的技术支持。而从技术层面上充分发掘潜力,以期实现战术-技术的完美结合,才更有利于战术目标的实现。

[1]刘良权.舰载信息系统[M].大连:海军大连舰艇学院,2002

[2]曲宝忠.海军战术导弹试验与鉴定[M].北京:国防工业出版社,2005,9

[3]夏洁.满足战场需求的实时飞行路径规划[J].北京航空航天大学学报,2004(2)

[4]陈谋.基于改进蚁群算法的无人机三维航路规划[J].吉林大学学报,2008(4)

[5]陈力.基于粒子群优化的航路规划算法研究与仿真[J].海军航空工程学院学报,2008(5)

[6]郭颖辉.基于遗传算法的飞行航路规划[J].计算机仿真,2004(2)

[7]殷人昆.数据结构[M].北京:清华大学出版社,1999,7