基于AHP的给水管网漏损影响因素分析
苏文龙
随着城市的不断发展,供水量越来越大,内部压力将逐步增大,很容易造成给水管网漏损,使供水系统的安全可靠性降低。
采用层次分析法分析给水管网漏损各个影响因素,确定各因素权重,为给水管网漏损深入研究提供了一种新思路,为给水管网的建设、设计、施工、管理提供了科学依据。
1 层次分析法(AHP)介绍
1.1 层次分析法的基本思想和原理[1]
层次分析法(The Analytic Hierarchy Process,简记AHP)是美国著名的运筹学家T.L.Satty等人在20世纪70年代提出的一种实用的多准则决策方法。层次分析法是指将决策问题的有关元素分解成目标、准则、方案等层次,在此基础上进行定性分析和定量分析的一种决策方法。这一方法的特点,是在对复杂决策问题的本质、影响因素以及内在关系等进行深入分析之后,构建一个层次结构模型,然后利用较少的定量信息,把决策的思维过程数学化,从而为求解多目标、多准则或无结构特性的复杂决策问题,提供一种简便的决策方法。
层次分析法不仅简化了系统分析和计算,还有助于决策者保持思维过程的一致性,是一种模拟人的思维过程的工具。
1.2 层次分析法的基本步骤[2,3]
1)明确问题。确定评价范围和评价目的、对象;筛选评价对象的影响因子;进行评价对象的影响因素、因子的相关分析,明确各影响因素、因子之间的相互关系。
2)建立层次结构模型。层次结构模型从上到下分为最高层A、中间层C、最低层 P。最高层A只有一个元素,表示系统所要达到的目标;中间层C表示采用某种措施和政策来实现预定目标所涉及的中间环节;最低层P表示与目标相关的若干影响因子,也叫方案层或指标层等,如图1所示。
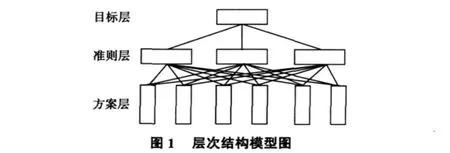
3)重要性等级确定。在进行多因素的管网漏损影响因素分析中,有定性因素,又有定量因素,各因素的重要程度不同,关联程度各异。层次分析法针对这些特点,对其重要程度作如下定义:
以相对比较为主:从第二层开始,针对上一层某个元素,对下一层与之相关的元素,进行两两比较,并按其重要程度评定等级。记 aij为i元素比j元素的重要性等级。
遵循一致性原则:当 i元素比j元素重要、j元素比k元素重要,则认为i元素一定比k元素重要。
4)构造判断矩阵。在每一层次上,按照上一层次的对应准则要求,对该层次的元素(指标)进行逐对比较,依照规定的重要性等级定量化后,写成矩阵形式,即A=[aij],A即为判断矩阵。其中aij>0,aii=1且aji=1/aij,即 A是正互反矩阵。构造判断矩阵是层次分析法的关键步骤。判断矩阵构造的方法有两种:专家讨论确定和专家咨询确定。为了使判断定量化,引用Staaty提出的1~9标度方法,见表1。

表1 判断矩阵标度及其含义
5)层次排序计算及权重计算。层次分析法的基本计算是计算判断矩阵的最大特征根及其对应的特征向量,然后再检验所构造的判断矩阵的一致性。层次单排序及权重计算的实质是计算出各判断矩阵的最大特征值及特征向量,经归一化后,即为同一层次相应因素对于上一层次某因素相对重要性的排序权值。
层次总排序即计算同一层次所有因素对于最高层(目标层)相对重要性的排序权值。重复以上步骤,计算C层对于A层以及P层分别对于C层和A层的相对重要性次序权重值,其中P层对于A层的权重值实际上是P层对于C层与A层对于C层权重值的累积值,为组合权重(Wi,PA=Wi,AC×Wi,CP)。这一组合权重即为P层相对于A层的重要性次序的权重值,据此排序。
最大特征根及其特征向量的计算其精确算法可以用线性代数中求矩阵特征根的方法求出所有的特征根,然后找一个最大的特征根,并找出它所对应的特征向量。此方法当判断矩阵的阶数n较高时,就要求解λ的n次方根且要把所有的n个特征根都找到,才能比较其大小,所以给计算带来了一定的困难。鉴于判断矩阵的特殊性,下面给出一种比较简单的近似计算。
AHP计算的方根法:计算步骤如下:
a.计算判断矩阵每一行元素的乘积 Mi:

b.计算 Mi的n次方根 ¯Wi:

c.对向量¯W正规化:
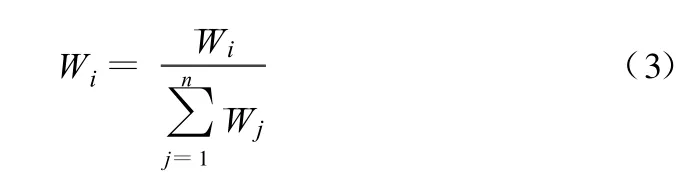
则W=[W1,W2,…,Wn]T即为所求的特征向量。d.计算判断矩阵的最大特征根λmax:

其中(AW)i表示向量AW的第i个元素。
6)一致性检验。在构造判断矩阵时,因专家在认识上的不一致,须考虑层次分析所得结论是否基本合理,需要对判断矩阵进行一致性检验,经过检验后得到的结果即可认为是可行的。
设CI为一致性指标,RI为一致性指标均值,CR为一致性比率。
a.单个判断矩阵一致性检验的算法为:

RI可根据矩阵阶数查表2获得:

如CR<0.1,认为判断矩阵具有满意的一致性。
其中,n为判断矩阵阶数;λmax为判断矩阵最大特征根;RI为当指标数为n时的平均随机一致性指标(见表2)。

表2 RI值
b.判断矩阵的整体一致性检验的算法为:
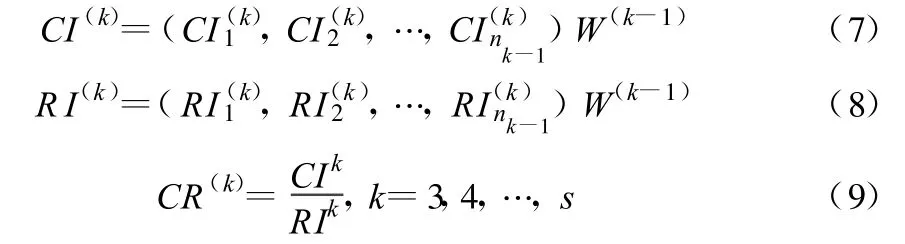
2 基于AHP的给水管网漏损因素评价模型的建立[3,5,6]
2.1 给水管网漏损影响因素
给水管网漏损的外在影响因素是指人为因素。由于人为因素没有一定的规律可循,所以在模型中不予考虑。
给水管网漏损的内在影响因素,在本文指管网自身特性及环境影响因素,包括:管材、管径、管道使用时间、管网的压力、埋深等。
2.2 层次分析结构模型的建立
根据各影响因素之间的关系,创建层次分析模型图(见图2)。

3 基于AHP的给水管网漏损因素评价模型的求解
3.1 构造判断矩阵
通过专家咨询,确定各影响因素的相对重要程度。按1~9标度法列出各层各元素的判断矩阵,如表3所示。

表3 判断矩阵
3.2 求解判断矩阵
经计算,判断矩阵A—C结果如表4所示。

表4 计算结果
判断矩阵一致性检验:经计算 λmax=5.037,根据式(7),式(8),计算得 CI=0.009,RI=1.12,根据式(9),计算得 CR=0.008<0.10,即完全满足一致性指标。由表3可以看出,C层各元素对应A层元素的排序权值分别为0.159,0.397,0.048,0.318,0.077,排序权值即为相对重要性。所以C层各元素对于A层的相对重要性由高到低排序为C2>C4>C1>C5>C3。
4 结语
1)用层次分析法对给水管网漏损因素进行分析,其结果体现出影响因素对漏损的影响程度的大小。城市给水管网中,管材、管径、埋深、压力、管龄中对管网渗漏影响的大小次序为管径>压力>管材>埋深>管龄,即对管网漏损影响作用的大小次序。2)对管网漏损影响因素进行层次分析的主要目的还是为更好地防治管网漏损。因此,我们可以根据管网漏损影响因素相对重要性建立管网漏损预测模型,这必将会大大提高预测模型的精度,更为有效地尽早发现可能的渗漏点,从而减少城市自来水的浪费。
[1]杜 栋,庞庆华.现代综合评价方法与案例精选[M].北京:清华大学出版社,2005:1-33.
[2]陈来安,陆军令.系统工程原理与应用[M].北京:学术期刊出版社,1988:191-204.
[3]王 研,何士华.多目标层次分析法评价区域水资源可持续利用[J].云南水力发电,2004,20(1):5-8.
[4]陈 沐.供水管网优化研究概述[J].山西建筑,2009,35(23):200-201.
[5]张 勤,李广浩,张 智.给水管网渗漏影响因素关联度的灰色评价分析[J].给水排水,2006,32(2):27-30.
[6]李传哲.改进层次分析法在影响因素分析中的应用[J].节水灌溉,2006(5):47-52.

