苏通长江大桥主梁断面三分力系数的雷诺数效应

陶 奇,廖海黎,李明水,鲜 荣

(1.西南交通大学风工程试验研究中心,成都 610031;2.广东公路建设有限公司,广州 510600)

0 引 言

桥梁断面的静力三分力系数是反映桥梁断面在风的静力作用下的三个分量,并仅与断面气动外形有关的无量纲气动参数。在桥梁抗风研究中,它是抖振响应分析、驰振稳定性分析以及静风荷载和稳定性分析中的重要参数,它的取值直接影响桥梁抗风分析的精度,因此,准确测定三分力系数对大跨桥梁抗风设计来说至关重要。

长期以来,人们一直认为具有尖锐棱角的桥梁断面三分力系数的雷诺数效应可以忽略不计。Schewe等[1]在压力风洞中测量了大海带桥引桥断面的三分力系数,发现雷诺数Re=7×104时的阻力系数比雷诺数Re=3×106时的阻力系数大14%,许志豪等[2]在测量香港昂船洲大桥三分力系数时,发现该桥在零度迎风角时其主梁断面的阻力系数随雷诺数增加而增加,陈斌[3]、李加武[4-5]和白桦[6]等也均通过风洞试验或CFD研究指出雷诺数对桥梁断面三分力系数有较大影响,不容忽视。笔者现场实测了苏通长江大桥主梁断面静力三分力系数,并将其与Re为104量级下的风洞试验结果进行了对比,研究了苏通长江大桥主梁断面静力三分力系数的雷诺数效应。

1 实测系统

1.1 同步脉动测压系统简介

现场测压所用的仪器是自行研制的60路同步动态测压系统,可以同时获得60个测压孔的静态和动态压力数据。压力传感器采用的是美国SM公司生产的SM-552型压力传感器。系统采用在信号调节器中加采样保持器的串行A/D工作方式,配置如图1所示。60路压力传感器和信号调节器输出的电信号经多路切换器变为2路模拟信号,由A/D转换为数字量存入工控机。同步信号驱动信号调节器中的采保电路,保证获得同一时刻的压力值。软件系统管理各部件的协调工作。

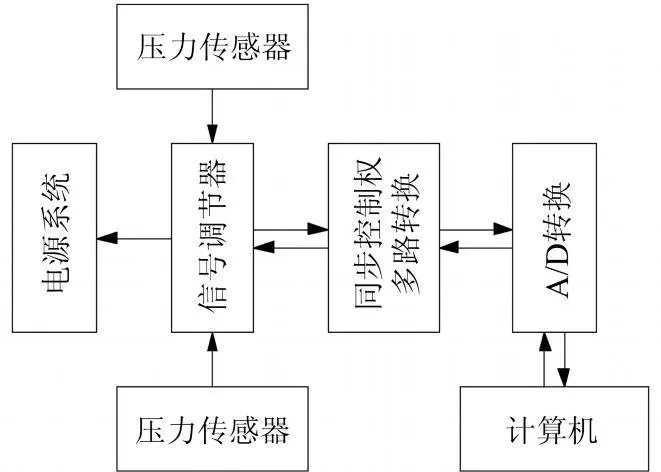
图1 60路动态测压系统Fig.1 The 60 channels dynamic pressure measurement system

为了防止雨水及合理地取得桥面表面的压力信号,特设计了一种π型压力感受器,如图2所示。为了应对现场复杂的环境,保护压力传感器,为每个传感器做了一个保护装置,如图3所示。

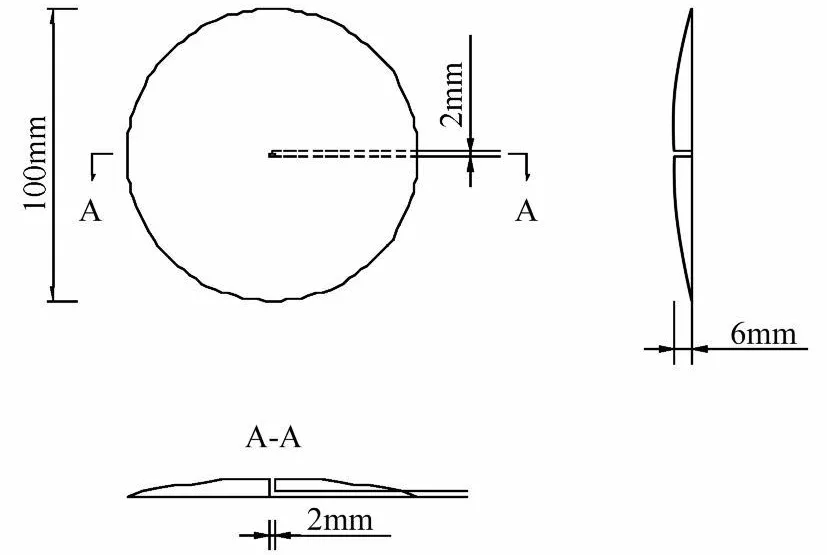
图2 π型压力感受器构造示意图Fig.2 The π-type structure diagram baroreceptor

图3 现场布置图Fig.3 The actually disposure

60路信号调节器做成二箱,每箱30路(其中一箱有10路接加速度传感器,压力传感器共用去50路),其中放大倍数四挡可选择,滤波器截止频率二挡可供选择。同步控制器和A/D板置于工控机内。数据由工控机采集下来后,可以很方便地利用计算机进行数据分析处理。

试验前必须对系统进行标定。压力标定系统由多路接头,数字压力计和压力泵组成,完成对系统的检查、压力的传递和对系统的标定。本系统的测压范围为0～±1000Pa,系统精度±1%,采样频率＞1kHz/ch。

测压系统中连接测压孔和传感器的是PVC塑料管道,由于测量的需要,PVC管道都具有一定的长度,当动态气流通过管道后,压力信号中的平均部分可以得到很好的传递,而脉动部分由于与管道的相互作用会发生畸变,从而导致脉动压力信号测量失真[7～8]。现场采用的是在30cm长的PVC管中加两个压扁铜管的方法来改善脉动压力的传递效果。该方法是改善脉动压力传递效果的简单而直接的方法[9]。由于本文着重考虑的是平均部分,因此改善脉动压力传递的方法这里不再详述。

1.2 三分力系数的定义

由各测压孔得到的风压积分,可以得到桥梁断面三个方向的气动力分量

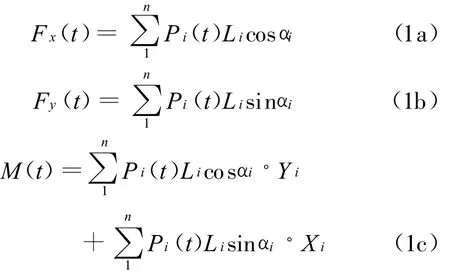
式中Fx(t)、Fy(t)、M(t)分别为体轴坐标系下单位长度上模型相对于扭转中心所受到的阻力、升力和升力矩时程;Li为第i点的积分长度;αi为第i点的内法线与桥面水平面的夹角;Xi与Yi是第i点与模型扭转中心的横向距离和垂直距离,如图4所示。静力三分力系数定义如下

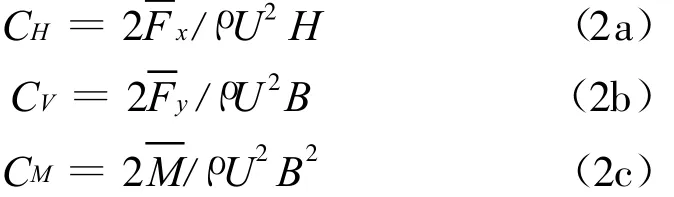
式中CH、CV和CM分别是体轴坐标系下模型的静阻力、升力和升力矩系数、和为(1)式中三个气动力分量的平均值;B为桥面宽度;U为平均风速;ρ为空气密度。只要在模型上布置的压力测点足够多,便可以准确测得桥梁断面的三分力系数。

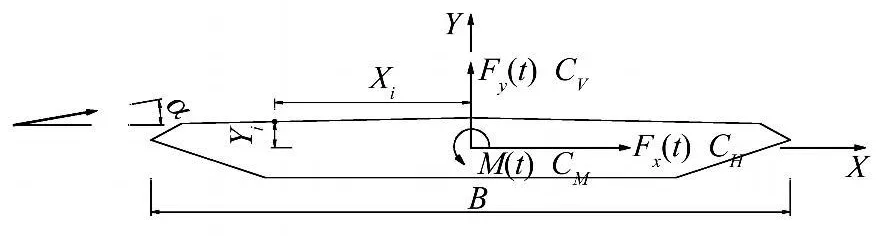
图4 三分力系数示意图Fig.4 Sketch of tri-component force coefficient

1.3 工程背景及测点布置简介

苏通长江大桥主桥为一座7跨钢箱梁斜拉桥,跨度布置为：100m+100m+300m+1088m+300m+100m+100m,大桥主跨为1088m。桥塔为混凝土结构,塔高300.4m。主梁为带风嘴的闭口钢箱梁,梁高为4.0m,主梁总宽度为41.0m,图5为该桥的总体布置图,图6为该桥施工过程中的主梁断面图。

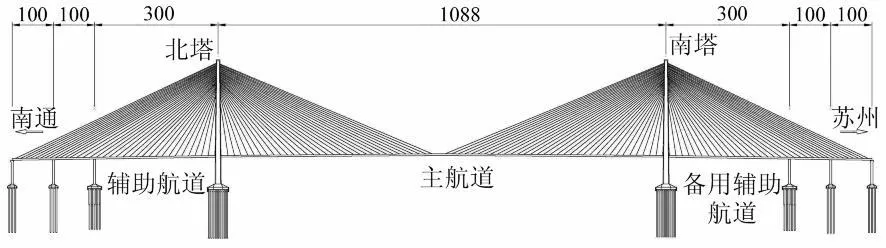
图5 总体布置(单位：m)Fig.5 General layout of Su-tong Yangtze River Bridge(unit：m)

测压法应尽量多地布置测点,以获得更好的积分结果。然而由于受到空间位置的限制和采集系统的限制(计算机内存,硬盘大小的限制),不可能布置太多的测点,综合了以上因素,最后确定沿桥梁断面表面布置50个测压点,风嘴部分平均相邻孔距为0.5m,其余部位平均相邻孔距为2m,如图7所示(另一边对称布置),测压断面位于跨中,距北塔329.3m处。

图7 断面测点布置图(单位：mm)Fig.7 Measure point distribution(Unit：mm)

2 实测结果与风洞试验结果的比较

在2007年5月～8月这3个月时间内对苏通长江大桥的主梁断面气动力进行了实时监控,从风速数据分析结果来看,强风方向与桥轴线垂直的情况很少见,而风洞试验时风向均垂直于桥轴线,由于风偏角β对三分力系数影响较大[10],因此,从所得结果中只选择了4个迎风角α和β风偏角 均较小的时间段来进行分析,如表1所示,风速时程长度取10分钟。

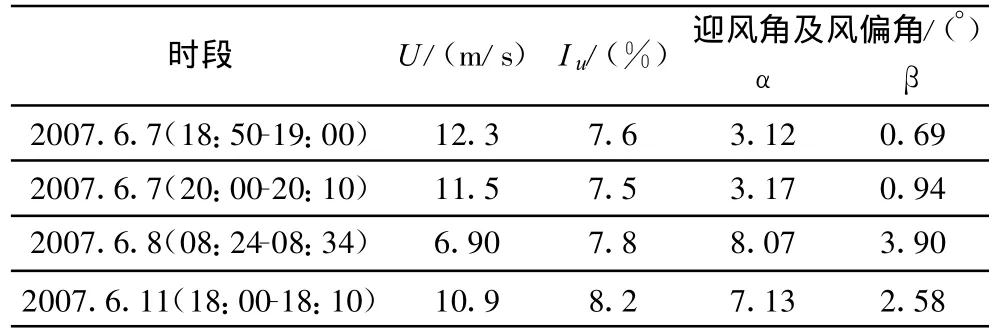
表1 平均风速、湍流度及风向Table 1 Average wind velocity,turbulence intensity and wind direction

由于影响三分力系数的非定常因素除了雷诺数外还有自然风的湍流强度及湍流积分尺度与结构特征尺寸的比值[3],因此,风洞试验结果也是基于湍流场采用测压法所测得结果,对于湍流积分尺度与结构特征尺寸的比值来说,国内学者陈斌等人认为其对三分力系数几乎没有影响[3],因此,没有仔细考虑。在模拟湍流场时分别采用了尖塔湍流场和格栅湍流场来模拟表1的湍流强度。测压模型的比尺为1：80。

图8给出了迎风角为3.12°时平均压力系数实测结果和实验室尖塔湍流场下的测量结果。利用该图按照式(1)进行积分,便可得到桥梁断面的三分力,再利用(2)式便可以得到主梁断面的三分力系数。

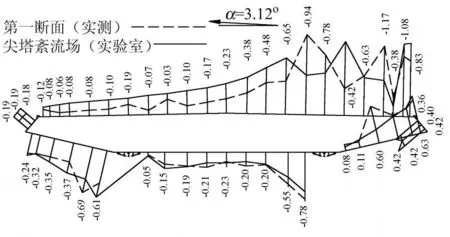
图8 实测与实验室平均压力系数分布Fig.8 Mean pressure coefficient distribution of actual test and wind tunnel test

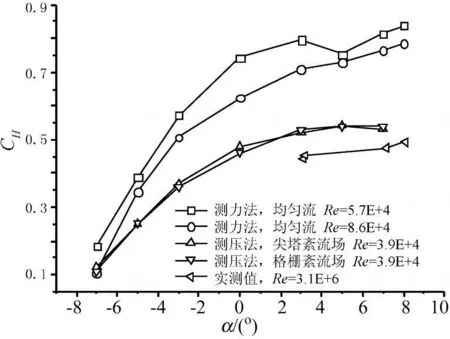
图9 阻力系数随迎风角的变化曲线Fig.9 Drag force coefficients vs.attack angle

图9～11给出了对应的静力三分力系数随迎风角的变化曲线。从图上可以看出阻力系数随雷诺数变化比较明显,实测值比风洞试验值小约15%,升力系数及力矩系数受影响较小,且格栅湍流场(≈0.082m,≈0.044m)风洞试验结果与尖塔湍流场(≈0.50m,≈0.41m)风洞试验结果差别不大,表明湍流积分尺度与结构特征尺寸的比值的确对三分力系数影响不大,这与陈斌等人的观点一致。

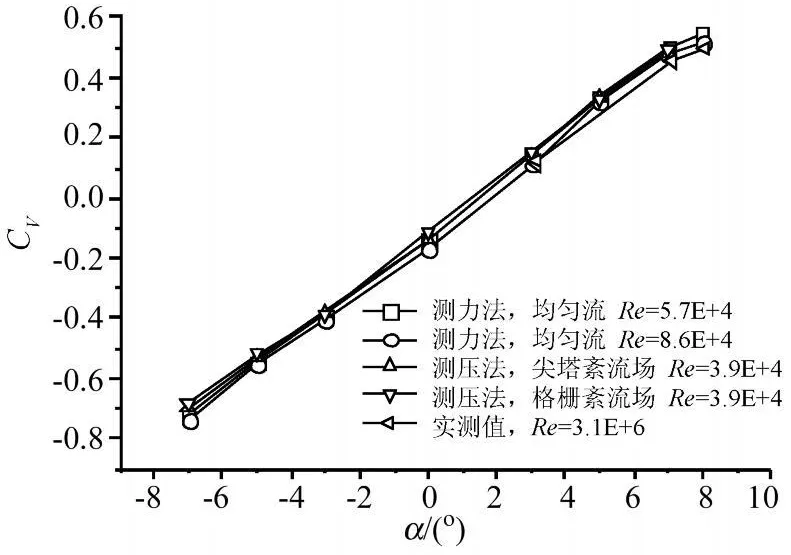
图10 升力系数随迎风角的变化曲线Fig.10 Lift force coefficients vs.attack angle

图11 力矩系数随迎风角的变化曲线Fig.11 Moment coefficients vs.attack angle

3 结 论

总结上述静力三分力系数实测及风洞试验测量结果不难发现：雷诺数对苏通长江大桥主梁断面阻力系数有较大影响,对升力系数及力矩系数影响较小。由于阻力系数的实测值明显低于风洞试验结果,因此,对苏通长江大桥来说,其阻力系数风洞试验结果偏于保守。

[1]SCHEWE G,LARSEN A.Reynolds number effects in the flow around a bluff bridge deck cross section[J].Journal of Wind Engineering and Industrial Aerodynamics,1998,74-76：829-838.

[2]MICHAEL C H H,LARSEN A.Aerodynamic investigations for the deck of stonecutters bridge emphasizing Reynolds number effects[A].Proceedings of the 2nd International Symposium on Advances in Wind&Structures[C].Busan Korea：Elsevier Publication,2002,649-656.

[3]陈斌,葛耀君,项海帆.非定常因素对静力三分力系数测量的影响[A].第十三届全国结构风工程学术会议论文集[C].大连：大连理工大学出版社,2007,556-561.

[4]李加武,林志兴,项海帆.桥梁断面三分力系数的雷诺数效应[J].同济大学学报(自然科学版),2004,32(10)：1328-1333.

[5]李加武.桥梁断面雷诺数效应及其控制研究[D].上海：同济大学土木工程学院桥梁工程系,2003.

[6]白桦,李加武,胡兆同,刘健新.近流线型断面静力三分力系数的雷诺数效应识别[J].建筑科学与工程学报,2007,24(4)：60-63.

[7]谢壮宁,顾明,倪振华.复杂测压管路系统动态特性的通用分析方法[J].同济大学学报(自然科学版),2003 31(6)：702-708.

[8]王维新,谢壮宁.测压传压管路系统动态特性的试验分析[J].西北大学学报(自然科学版),2005,35(4)：702-708.

[9]MOCK E B.The UEDAH multi-channel simultaneous fluctuating pressure measurement system and its applications[J].J Wind Eng.And Aerodynamic,1994,(51)：93-104.

[10]刘小兵,陈政清,刘志文.斜风下大跨度桥梁主梁三分力系数试验研究[J].湖南大学学报(自然科学版),2008,35(9)：10-14.