激波与氦气泡相互作用的实验与数值研究
黄 甲,贾洪印,罗喜胜,杨基明,邹立勇,谭多望
(1.中国科学技术大学近代力学系,合肥 230027;2.中国工程物理研究院流体物理研究所冲击波物理与爆轰物理实验室,四川绵阳 621900)
0 引 言
当激波穿过不同流体界面时,由于界面两边密度等参数的不同,在具有脉冲特征的激波驱动下流体界面会呈现出复杂的流动现象。其中最为典型的现象之一是,界面上的扰动会随时间急剧增长,并最终导致两种流体之间强烈的相互混合,即所谓的Richtmyer-Meshkov不稳定性(简称R-M不稳定性)[1-2]。这种激波-界面的相互作用不仅在界面运动稳定性、旋涡以及湍流形成机理方面有着重要的学术意义,在发动机中的混合和燃烧、超新星的爆发、惯性约束热核聚变以及与掺混有关的工程实际等领域也具有重要的应用价值。
对于R-M不稳定性,目前的理论模型主要有Richtmyer的脉冲模型理论和可压缩线性理论[1],以及Zhang和Sohn等的非线性理论[3]等。实验研究方面,最早由Meshkov完成了验证性的实验[2];其后Benjamin进行了Air-SF6和Air-He激波管实验[4];Haas和Sturtevant进行了平面激波与球形界面、柱形界面相互作用的实验[5]。Jacobs采用气柱方式生成气-气界面,并运用PLIF技术,开展了一系列的研究工作[6]。美国威斯康星大学Bonazza小组用竖式激波管,开展了R-M 不稳定性实验[7]。日本东北大学的Takayama小组利用竖式激波管产生柱形汇聚激波,研究了肥皂泡形成的气-气界面的R-M 不稳定性[8]。与国外同行相比,国内有关R-M不稳定性的研究较少,且多集中于数值模拟方面[9-13],实验方面的工作就更少了[14-15]。
对于球形界面的R-M不稳定性问题,由于激波会在交界面发生多次透射和反射,与研究较多的平面密度界面的R-M不稳定性问题相比,更为复杂。实验方面,对界面的生成和流场的观测也提出了更大的挑战,正是由于上述特点,使得这一问题的实验研究较少,而目前国内还尚未见到公开发表的实验结果。采用肥皂膜产生气体界面,利用阴影法,获得了一系列的实验结果,并与数值模拟结果进行了对比。
1 实验设备与方法
实验工作是在矩形激波管中进行的,其截面尺寸40 mm×70 mm。初始界面的生成采用在实验段吹氦气泡的方法,流动显示手段采用高压火花光源搭配传统的纹影法和阴影法。
1.1 球形界面的生成
由于表面张力的作用,肥皂泡会自然呈现出球形,所以本实验采用直接吹制的办法来生成球形氦气泡。首先将导气管安装在试验段下壁面的开口内,通过人工控制气阀从而以较稳定的气流速度生成球形氦气泡。试验中采用氦气泡直接悬挂于导气管端部的方式以保持其位置固定。观察窗尺寸为70 mm×150 mm。经过多次反复实验,采用恰当配方的溶液(配方为20%乐仔超大肥皂泡专用浓缩液,80%纯净水)。氦气泡内压力约为1.05×105Pa,吹制的球形氦气泡膜厚约为1μ m,在试验段可维持约3min的时间,基本满足实验的需求。
1.2 基于火花光源的纹影阴影系统
为了捕捉到激波与氦气泡相互作用后气体界面的变形,光学系统必须具备较高的瞬态图像捕捉能力。火花光源的闪光时间为微秒量级,因此采用阴影法和纹影法可以有效的捕捉到瞬态下界面的变形,从而达到将流场“冻结”并拍摄的目的。图1以纹影法为例,显示了实验中采用的激波管和测量系统。
实验中,激波管驱动段和被驱动段均采用空气。被驱动段初始压力为0.1MPa,破膜时驱动段压力为0.27MPa。当高压段和低压段之间膜片破裂后,形成一道入射激波沿被驱动段传播,依次经过两个压力传感器,其信号被示波器记录。根据激波到达两传感器的时间可以计算出激波的速度等流动参数,并计算得到激波到达试验段所需时间,从而可以控制高压电源的放电时刻。延时器按预设时刻发出电信号,触发高压电容进行放电,从而点亮火花光源瞬间发光。此时激波通过试验段流场的纹影或阴影图像就被CCD相机记录,从而得到所需要的实验照片。

图1 实验及测量系统示意图Fig.1 Schematic of facility and measuring systems
2 数值模拟方法
为了获得更为丰富的流场信息,还通过求解二维轴对称的Euler方程,采用有限体积方法,结合网格自适应策略,对实验过程进行了数值模拟,并与实验结果进行了比较。
采用非结构的四边形网格作为计算网格,并采用MUSCL-Hancock格式以达到时间二阶,空间二阶的求解精度。其中非结构网格的自适应技术是数值模拟中所采用的一项比较关键的技术,通过自适应策略,使得网格在密度梯度大的区域自动细化,从而能更好地刻画出波系和气体界面的精细结构。有关程序的验证参见文献[16],这里不再赘述。
初始状态如图2所示,激波由右向左传播,X轴为对称轴。计算区域为250 mm×70 mm,激波马赫数采用实验测量的马赫数,即为1.2。初始网格大小为1.0 mm×1.0 mm,最高加密6层,即最小网格尺寸为15.625 μ m×15.625 μ m。氦气泡的初始半径为175 mm.

图2 初始时刻流场示意图Fig.2 The initial flow field
3 结果与分析
激波与球形氦气泡相互作用实验阴影和数值模拟纹影结果如图3所示。
从图3可以看出,在入射激波尚未到达时,氦气泡能保持很好的球形见图3(a);当激波与氦气泡相遇后,除了产生透射激波进入气泡内,还产生了反射波向上游传播。由于透射激波在氦气中传播,速度较入射激波在空气中传播要快,入射激波沿氦气泡表面连续发生透射和反射,透射激波逐渐弯曲并呈现出弧形。同时,由于激波的压缩作用,氦气泡经透射激波压缩的区域,在阴影照片中呈现出较深的颜色见图3(b);在图3(c)中,透射激波几乎已完全脱离界面,同时在激波的加速下,氦气泡的迎风面发生变形,逐渐向泡内弯曲;随着时间的推移,界面的迎风面向内弯曲越来越明显,在图3(d)中,氦气泡已经由最初的球形变为椭球形。相对而言,背风面部分在前期阶段仍能保持较好的球面形状。这与Hass和Sturtevant[5]的实验是一致的。
在图3(f)中,流场中已看不到入射激波,而氦气泡的右侧则出现"尖钉"结构,这表明周围的空气开始进入到氦气泡中,两种气体之间开始出现明显的混合。而在图3(g)中,原本还不大明显的尖钉此时已经发展得比较明显。尖钉呈现出蘑菇头状,同时尖钉头部的上下两侧出现了一对旋涡形状的结构,非线性阶段的特征表现得比较明显。由此可以判断在图3(e)和图3(g)之间,可能是界面由线性阶段向非线性阶段发展的重要转折点。而此时氦气泡的右侧面则已经向内深深地凹陷,并逐渐向左侧界面靠拢。
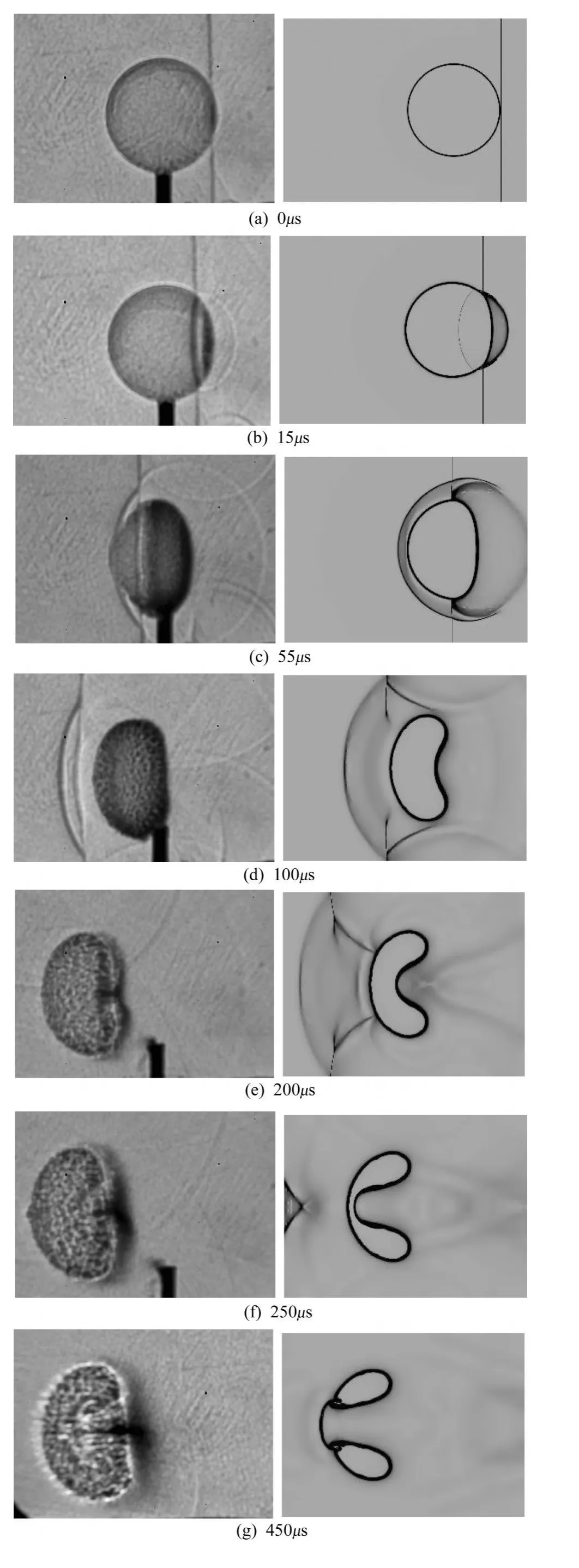
随着界面的进一步发展,尖钉不断向左移动,并最终与氦气泡的左侧界面相遇。整个氦气泡如同两片肺叶,从中间分隔开。而在图3(g)中位于氦气泡中心位置的旋涡状结构此时已经移动到头部,同时旋涡的尺度也有所增加。这是因为当界面发展出"尖钉"结构并从氦气泡右侧向左侧面移动时,由于涡的自旋效应,不断将周围的涡量卷吸进去,使得涡的尺度逐渐增大,进一步加剧了界面的变形和两种气体之间的混合。与Layes等人的实验照片[17]比较,从波系结构以及界面变形和发展的趋势来看,二者表现得很一致。

图3 激波与球形氦气泡相互作用:阴影实验照片(左)和数值纹影(右)。Fig.3 The shock-bubble(helium)interaction:experimental shadowgraph(left)and numerical schlieren(right)
数值计算结果也很好地表现出界面在激波作用下的演化过程,在初期与实验结果基本吻合,从而验证了该计算程序的可靠性。还可以发现,在发展后期如图3(e-h),非线性特征比较明显,湍流混合逐渐变强时,两者结果相差就比较大,这是因为所采用的计算方法还不能完全描述后期非线性特征。尽管如此,仍然可以根据数值计算结果,对界面的发展,失稳过程进行详细的分析。下面给出几个时刻涡量的分布云图。
从涡量云图中可以看到,涡量的产生主要集中在氦气泡的表面,这是由于本实验中,只有在氦气泡的表面密度梯度和压力梯度是不平行的。密度梯度和压力梯度的不平行会导致涡量的产生。同时这也表明在激波与界面的相互作用过程中,斜压机制是导致涡量产生的主要因素。
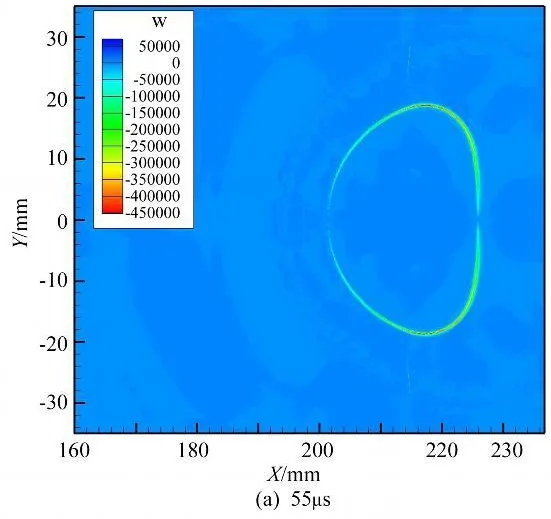
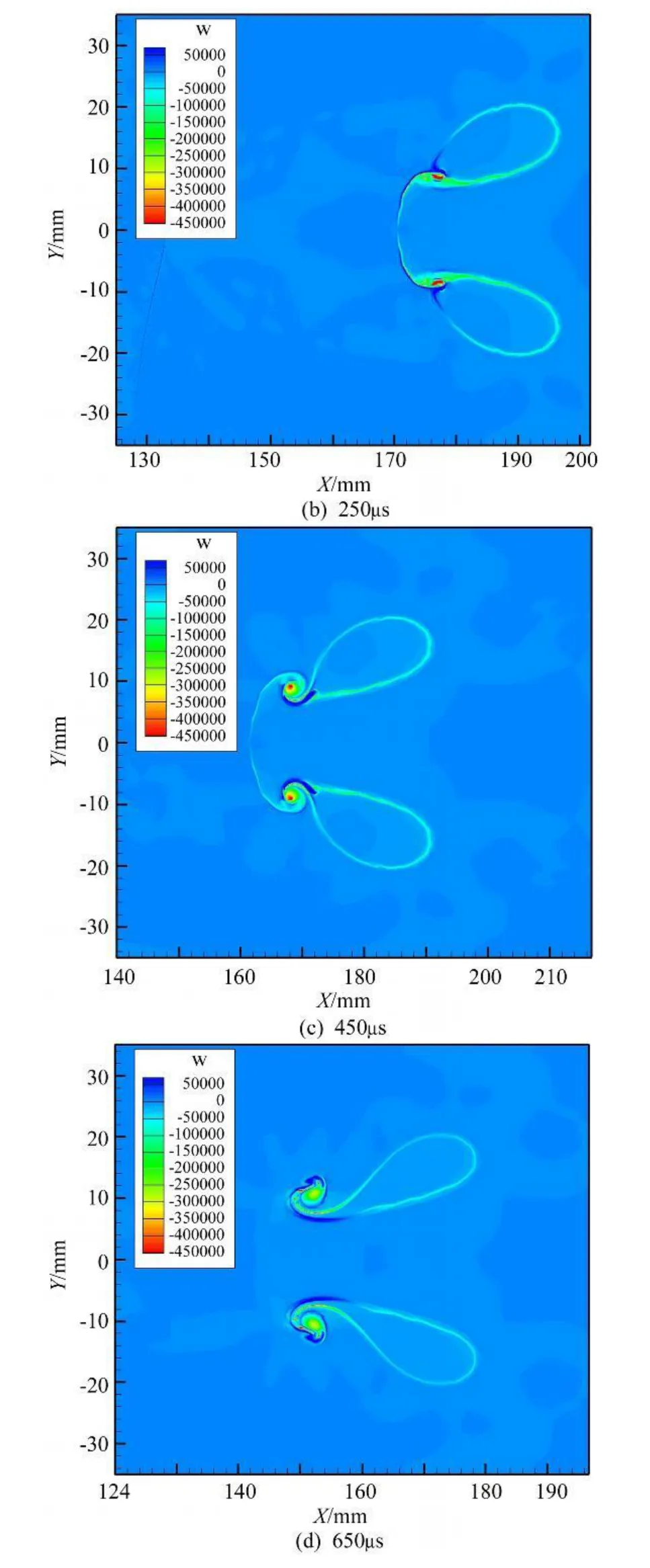
图4 不同时刻的数值涡量云图Fig.4 Vorticity contours at four instants by numerical results
在图4(a)中可以可到,在激波与氦气泡开始接触的地方,涡量几乎没有产生,这是由于此时压力梯度与密度梯度平行,斜压项为零。随着激波向左运动,入射激波、透射激波和反射波所产生的压力梯度与界面的密度梯度不平行,涡量变大。相比入射激波,透射激波对涡量的贡献很小。在图4(b)中,入射激波已经完全经过氦气泡,此时涡量呈现出在氦气泡右侧表面聚集的趋势,同时"尖钉"结构开始显现。可见"尖钉"的产生和发展与涡量的分布有着密切关系。由于旋涡诱导的旋转运动,涡量在表面的聚集会导致界面发生各种变形,而反过来界面的变形又会进一步影响到涡量的分布见图4(c)和(d),这种强烈的相互耦合正是在R-M不稳定性中界面发生不稳定性的一个主要特征。
4 结论与展望
在激波管中开展了球形界面R-M不稳定性的实验和数值研究,获得了一系列的结果,并与国外同行的结果进行了比较,较为一致。
在激波的加速下,氦气泡迎风面先发生变形,氦气泡由初始的球形逐渐变为椭球形,在随后的过程中,周围的空气开始进入到氦气泡中,形成尖钉结构。随时间推移,尖钉呈现蘑菇状,同时在尖钉的上下两侧形成一对旋转方向相反的旋涡结构,进一步加强两种气体之间的混合。而在与数值模拟的结果相比较中可以看出激波所产生的压力梯度与界面原有的密度梯度的不平行是导致涡量产生的主要来源。入射激波经过后,分布在氦气泡表面的涡量会在旋涡诱导下发生聚集,产生尖钉结构和蘑菇头。由此可见涡量的产生和分布对于界面的变形和失稳有着重要的影响。
与计算的结果相比,实验结果中界面的变形速率要小一些。下一阶段我们将进一步完善氦气泡的制作工具,从而减小氦气泡的大小与氦气纯度波动的影响,并将引入激光全息干涉、激光诱导荧光或纳米散射等显示技术,获得更为全面、精细的流场结构信息。同时改进数值方法,以期能正确描述发展后期界面的非线性行为。
本工作得到翟志刚同志的大力协助,特此感谢。
[1]RICHTMYER R D.Taylor instability in shock acceleration of compressible fluids[J].Commun.Pure Appl.Math,1960,13:297-319.
[2]MESHKOV.Instability of the interface of two gases accelerated by a shock wave[J].T ransl.of Izv.Acad.Sci.USSR Fluid Dyn.,1969,4:101-104.
[3]ZHANG Q,SOHN S.An analytical nonlinear theory of Richtmyer-Meshkov instability[J].Physical Letter A,1996,212:149-155.
[4]BENJAMIN B,BESNARD D,HAAS J.Shock and reshock of an unstable interface[M].LA2UR 9221185,1993.
[5]HAAS J F,STURTEVAN B.Interaction of weak shock waves with cylindrical and spherical gas inhomogeneities[J].J.Fluid Mech.,1987,181:41-76.
[6]JACOBS J W.Shock-induced mixing of a light-gas cylinder[J].J.Fluid Mech.,1992,234:629-649.
[7]ANDERSON M H,PURANIK B P,OAKLEY J G,et al.Shock tube investigation of hydrodynamic issues related to inertial confinement fusion[J].Shock Waves,2000,13:377-387.
[8]HOSSEINI S H,TAKAYAMA K.Experimental study of Richtmyer-Meshkov instability induced by cylindrical shock waves[J].Phys.Fluids,2005,17:084101.
[9]马东军,何兴,孙德军,等.柱状交界面 Richtmyer-M eshkov不稳定性的数值研究[J].爆炸与冲击,2003,23(5):398-404.
[10]程军波,傅德薰,马延文.Richtmyer-Meshkov失稳的数值模拟[J].计算物理,2001,18(5):390-396.
[11]柏劲松,陈森华,钟敏.界面不稳定性的自适应欧拉数值计算[J].爆炸与冲击,2003,23(1):19-24.
[12]姜洋,赵宁,唐维军.界面不稳定性数值模拟中的虚拟流动方法[J].计算物理,2003,20(6):549-555.
[13]谢正桐,李家春,王丽丽.R-T界面不稳定性及湍流混合的大涡模拟[J].计算物理,2002,19(2):108-114.
[14]卓启威,施红辉.气/液界面上 Richtmyer-Meshkov不稳定性的实验研究[J].实验流体力学,2007,21(1):25-30.
[15]邹立勇,刘金宏,王建,等.一个用于界面不稳定性实验研究的竖式激波管[J].高压物理学报,2008,22(2):197-202.
[16]SUN M,TAKAYAMA K.Conservative smoothing on an adaptive quadrilateral grid[J].J.of Comp.Phys.,1999,150:143-180.
[17]LAYES G,JOURDAN G,HOUAS L.Distortion of a spherical gaseous interface accelerated by a plane shock wave[J].Phys.Rev.Lett.,2003,91:174502.

