不同尾翼鸭式布局远程弹在跨/超声速的气动特性实验研究

邓 帆,陈少松,谭献忠,徐 涛

(1.南京理工大学动力工程学院,南京 210094;2.南京模拟技术研究所,南京 210016)

0 引 言

炮射的远程弹由于结构的制约需要采用鸭式布局外形,为了提高滑翔增程的效率,舵面最好始终呈×形布置飞行,这就要求在弹道的滑翔段进行滚转控制,而鸭式布局条件下的滚转控制是弹箭气动布局研究的难点[1],鸭舵引起的非对称下洗流场在尾翼上产生反效诱导滚转力矩,随着布局形式、马赫数以及迎角的变化其影响程度不同。通常滚转反效主要发生在跨声速和低超声速范围内,而远程弹的滑翔控制正是在高亚声速、跨声速和低超音速段,因而有部分速度处于滚转控制反效范围内。鸭式布局的设计对减小这种滚转反效有一定的作用[1,4],采用“断牙”形状的鸭舵或者是在鸭舵前布置翼前小翼对于减小滚转反效是有利的,鸭舵在弹身上的位置对滚转反效也有影响;尾翼对鸭舵引起的滚转反效影响很大,在俯仰控制允许的条件下,减少尾翼的展长对减小滚转反效是有利的,在尾翼上添加副翼或是沿尾翼展向吹气都是有效的办法,但是对于尺寸相对较小又要进行滑翔的远程弹来说这些方法实现起来有困难;自旋尾翼在鸭舵下洗产生的反效滚转力矩作用下旋转从而不会使其传递到弹身上,是克服鸭舵下洗的好方法,“T”型尾翼上的小翼能起到副翼的作用,也能有效减少下洗诱导滚转力矩,提高鸭舵的滚动控制效率[2-5],但是“T”型尾翼的形式多样,减少下洗诱导滚转力矩的效果不尽相同;栅格翼是一种新型的弹翼,它由很多栅格组成,气动特性规律比较独特,将栅格翼作为鸭式布局尾翼的可行性值得研究[6,7]。

设计了一种“T”型尾翼和一种栅格尾翼鸭式布局模型,为了研究两种模型的气动特性,特别是滚转控制气动特性,还设计了无尾翼鸭式布局模型,通过风洞测力实验研究了三种模型的气动特性,特别是对“T”型尾翼和栅格尾翼鸭式布局的滚转特性与无尾翼模型的滚转特性进行了比较,同时对纵向气动特性的变化也进行了详尽的分析,力求在减小鸭式布局诱导滚转力矩的同时,尽量不改变其纵向气动特性。研究结果对提高远程弹的滑翔增程效率有重要的参考价值。

1 实验方法

实验是在南京理工大学HG-4号风洞中进行的。HG-4号风洞为直流下吹暂冲式闭口超声速风洞,实验段截面尺寸为300mm×300mm,实验段长为600mm;风洞有迎角机构,用于支撑天平和模型,并用来改变模型迎角;实验段两侧开有290mm×160mm的光学玻璃观察窗,供在实验过程中观察模型姿态或进行纹影照相;并配有六分量天平、纹影仪以及常规实验设备,采用更换喷管的方式改变马赫数。

实验采用六分量气动天平,将模型安装在天平支架上,天平支撑于迎角机构上,这样可以实现一次吹风过程中连续改变迎角,迎角a变化范围-4°～8°,实验马赫数的范围0.8～2.5。

2 实验模型

2.1 无尾模型

设定未安装弹尾的模型代号为W,舵片采用俯仰舵和差动舵的组合,俯仰舵水平放置,差动舵舵片净展长为27.2mm,,规定从左视图方向看去上鸭舵右偏(此时下鸭舵左偏)时δ为正,反之为负,一般正的差动偏角产生负的滚转力矩,3个模型的舵偏角δ均为-10°,两组舵片厚度均为0.8mm,具体参数见图1。

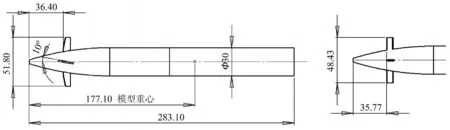
图1 W模型工程示意图(上视图及弹头前视图)Fig.1 The engineering drawing of model W(top view and front view of the missile′s head)

图2 T模型安装姿态示意图Fig.2 The sketch of model T

2.2 “T”型尾翼模型

设定W模型加接上长45mm的尾部,尾翼为“T”型翼的组合模型代号为T,如图2。尾翼采用6片的“T”型尾翼,具体参数见表1。

2.3 栅格尾翼模型

设定W模型加接上长45mm的尾部,尾翼为栅格翼的组合模型代号S,如图3。尾翼采用4片栅格翼,栅格翼中心剖面距弹底为7mm,具体参数见表2。

参考面积取弹体最大横截面积,S=706.86 mm2,参考长度取全弹长,l=328.1mm,全弹俯仰力矩系数的参考点取弹质心,滚转力矩系数的参考点取弹体轴。

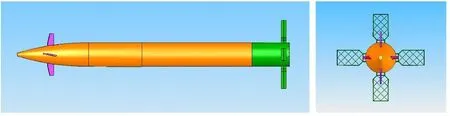
图3 S模型安装姿态示意图Fig.3 The sketch of model S

表1 “T”型尾翼基本参数表Table 1 Basic parameters of“T”shaped fins

表2 栅格尾翼基本参数表Table 2 Basic parameters of grid fins

3 实验结果和分析

3.1 阻力特性

图4给出的是三种模型的阻力系数CD在α=4°状态下随马赫数的变化曲线。从图中可见,三种模型的阻力系数CD随马赫数先增加再减小,在Ma=1时达到最大值,跨声速阶段的阻力系数值高于超声速阶段,这是由于波阻的影响;W模型的阻力系数最小,因为此模型无尾翼,迎风面积小于其他两个模型;S模型栅格尾翼的迎风面积为332mm2,T模型“T”型尾翼的迎风面积为218mm2,栅格翼的迎风面积远大于“T”型翼,由图4可知S模型的阻力系数CD约高于T模型67%;与“T”型翼不同的是,栅格翼由于自身的特殊栅格结构所以阻力系数相对较大,超声速后,W模型和T模型的阻力系数都缓慢下降,而S模型的阻力系数在Ma=2后基本保持不变,对于栅格翼来说,阻力大一直是需要解决的问题。

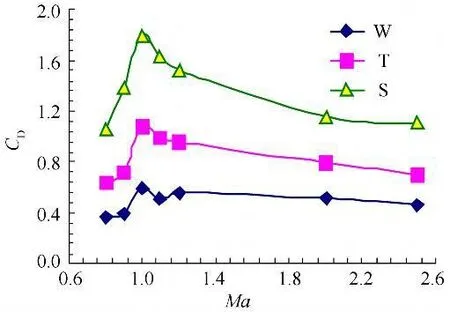
图4 α=4°,CD随Ma变化曲线Fig.4 CDvs Mach(α=4°)

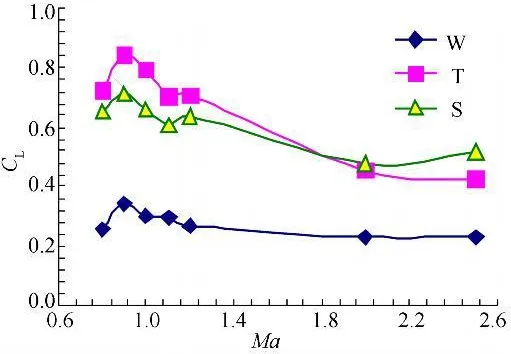
图5 α=4°,CL随Ma变化曲线Fig.5 CLvs Mach(α=4°)

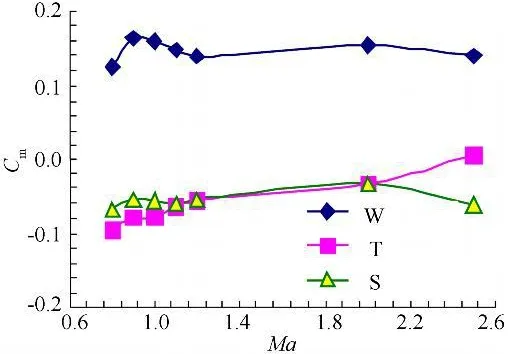
图6 α=4°,Cm随Ma变化曲线Fig.6 Cmvs Mach(α=4°)

3.2 升力特性

图5给出的是三种模型的升力系数CL在α=4°状态下随马赫数的变化曲线。由图可见三种模型的升力系数CL在Ma=0.9时达到最大值,超声速阶段W模型和T模型的升力系数都呈减小的趋势,而S模型的升力系数在Ma=2后开始逐渐回升;W模型升力最小,T模型和S模型的升力系数相差无几,在跨声速区域内,T模型的升力系数略大于S模型;而在超声速区域,情况刚好相反。由于栅格翼的结构比“T”型翼复杂得多,栅格壁之间存在的相互影响使得S模型在跨声速时弹体周围流场更加复杂,产生的激波封口造成气流壅塞,使得升力系数较小;超声速阶段,当马赫数达到一定值使得栅格翼的激波脱出栅格边框,不再在栅格内部反射后,栅格翼的升力系数回升,表现出比“T”型翼更好的升力特性。

3.3 俯仰力矩特性

图6给出的是三种模型的俯仰力矩系数Cm在α=4°状态下随马赫数的变化曲线。由图可见在正迎角下T模型和S模型的俯仰力矩系数为负值,而W模型相反;图7显示Ma=2时T模型和S模型的俯仰力矩系数都随迎角增大而减小,大部分迎角下 T模型俯仰力矩系数绝对值略大于S模型;当马赫数继续增大,如图8所示,在Ma=2.5时,T模型的俯仰力矩系数变化幅度很小,并且俯仰力矩特性曲线对于横坐标轴的斜率近似为零,俯仰力矩系数开始变为正值,说明T模型转为纵向静中立稳定,而S模型的俯仰力矩系数仍为负值,并且绝对值增大,静稳定裕度还略有增加,说明栅格翼在超声速阶段的纵向静稳定性优于“T”型翼。

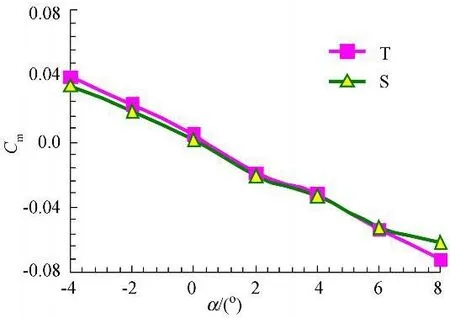
图7 Ma=2.0,Cm随α变化曲线Fig.7 Cmvs attack angles(Ma=2.0)

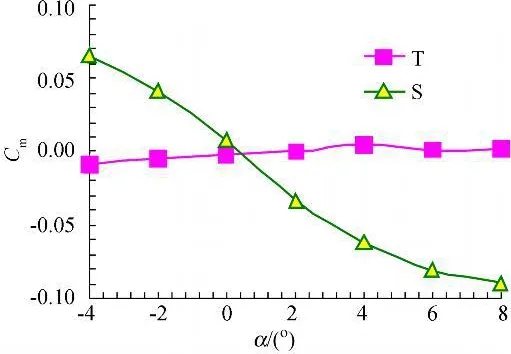
图8 Ma=2.5,Cm随α变化曲线Fig.8 Cmvs attack angles(Ma=2.5)

3.4 滚转力矩特性

图9给出的是三种模型的滚转力矩系数Cl在α=4°状态下随马赫数的变化曲线。W模型的设计是为了与另二组有尾翼模型做对比,由图可见W模型的滚转力矩系数均为正值,在Ma=1时达到最大,然后随着马赫数的增加而逐渐减小;T模型的滚转力矩系数在跨声速阶段出现负值,与鸭舵滚转控制力矩方向相反,并且在超声速时随着马赫数的增加其滚转力矩系数再次减小,到Ma=2.5后值为负,滚转力矩系数小于同迎角下W模型的值,W模型滚转力矩系数均为正值说明此模型可以很好地进行滚转控制,因为没有尾翼,鸭舵差动偏转进行滚转控制时产生的不对称下洗流场对自身无影响;安装“T”型尾翼后,在跨声速区域的小迎角范围内出现滚转控制反效的情况,其他情况下都可以有效的控制滚转。

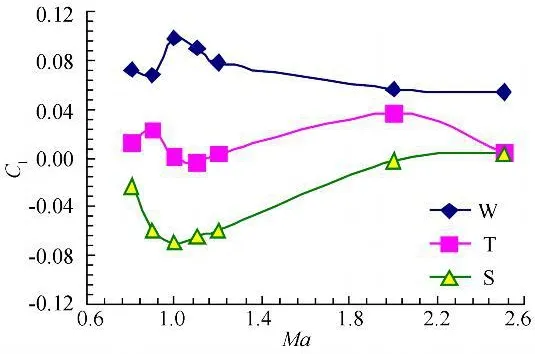
图9 α=4°,Cl随Ma变化曲线Fig.9 Clvs Mach(α=4°)

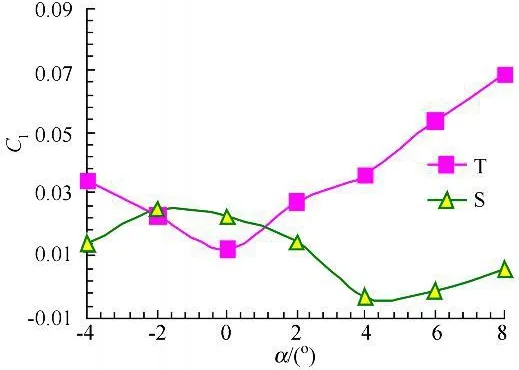
图10 Ma=2.0,Cl随α变化曲线Fig.10 Clvs attack angles(Ma=2.0)

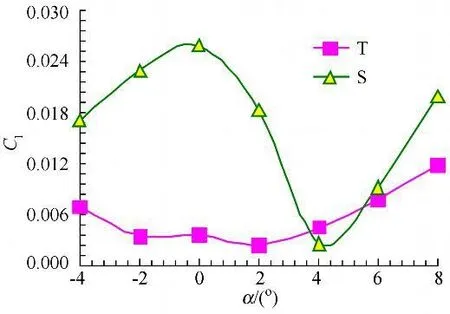
图11 Ma=2.5,Cl随α变化曲线Fig.11 Clvs attack angles(Ma=2.5)

跨声速阶段T模型和S模型的滚转力矩系数有正值也有负值,大部分迎角下T模型的滚转力矩系数大于S模型,因此T的滚转控制性能优于S模型;超声速阶段二者的滚转力矩系数随着马赫数的增加,T模型的优势逐渐减小。如图10和11所见,当Ma=2时,T模型的滚转控制性能在α=0°取得最小值,但从整个迎角范围来看优于S,当Ma=2.5时,大部分迎角下S模型更利于滚转控制。由此可见,“T”型尾翼与栅格尾翼各有所长,在其他条件相同的情况下,Ma≤2.0时,适合选择“T”型尾翼,Ma＞2.0时,栅格尾翼更利于滚转控制。值得注意的是,在跨声速阶段,虽然两者均产生滚转反效,但栅格尾翼产生的反效一致,“T”型尾翼反效不一致,从而采用栅格尾翼可以利用其在跨声速阶段反效一致的特性进行反向的滚转控制;在整个马赫数阶段,栅格翼在迎角α=4°时滚转力矩系数最小,α＜2°栅格翼对滚转力矩的控制效率较高。

4 结 论

通过风洞实验,研究了3种不同尾翼的鸭式布局远程弹的气动特性,尤其是滚转控制方面的性能,得出如下结论：

(1)无尾翼模型阻力小,能进行有效的滚转控制,但丧失了尾翼提供的升力。带“T”型尾翼的模型,升力和阻力都较大,但在跨声速阶段的小迎角区域难以进行滚转控制;

(2)“T”型尾翼模型和栅格尾翼模型相比,在跨声速阶段其升力特性优于栅格尾翼,也更利于滚转控制,超声速阶段栅格尾翼模型具有升力特性优势,同时也容易进行滚转控制,缺点是阻力较大;

(3)在跨声速阶段,虽然“T”型尾翼和栅格尾翼均产生滚转反效,但栅格尾翼产生的反效一致,T型尾翼反效不一致,从而可以利用栅格尾翼在跨声速阶段滚转反效一致的特性进行反向的滚转控制。

[1]BURT J R.The effectiveness of canards for roll control[R].AD/A 037077,1976.

[2]AUMAN L M.Aerodynamic characteristics of a canardcontrolled missile with a free-spining tail[R].AIAA98-0410,1998.

[3]BLAIR A B JR.Romote control canard missile with a free-rolling tail brake torque system[J].Journal of spacecraft and rockets,1981,18(6)：550-555.

[4]曾广存,丁庆国,秦伊贤等.鸭式布局导弹滚动气动控制方案及力矩分析[J].空气动力学学报,1988,6(3)：376-381.

[5]雷娟棉,居贤铭,吴甲生.自旋尾翼鸭式布局导弹的滚转特性[J].北京理工大学学报,2004,24(8)：657-659.

[6]DESPIRITO J.CFD investigation of canard-controlled missile with planar and grid fins in supersonic flow[R].AIAA 2002-4509,2002.

[7]DESPIRITO J.Subsonic flow CFD investigation of canard-controlled missile with planar and grid fins[R].AIAA 2003-0027,2003.