基于HGA的智能交通调度优化方法研究＊

刘长华 王 忠

（中国民航飞行学院飞行技术与飞行安全科研基地1） 广汉 618307） （四川大学电气信息工程学院2） 成都 610065）

公共车辆运营调度管理通常分为3个阶段完成：计划、调度和控制.调度是关键的中间环节，车辆运营调度问题就是针对一项可分解的运输任务，在一定约束下如何安排运作时间和先后顺序，以获得运输成本或时间最优化.公交车辆调度包括静态调度和动态调度，本文着重研究静态调度，即：运营车的发车时刻表的编排过程.采用智能化算法，即将免疫算法与遗传算法有机结合，提出一种改进型混合遗传算法来求解车辆调度优化问题，在有限的算法步骤内，找出所有满足约束条件的排班方案中的最优方案或接近最优的方案，从而可以提高公交企业的管理和服务水平.

1 调度的数学模型

遗传算法（genetic algorithms，GA）是一种基于自然选择和基因遗传学原理的自适应全局优化概率搜索方法.它的创立有2个研究目的：（1）抽象和严谨地解释自然界的适应过程；（2）为了将自然生物系统的重要机理运用到工程系统中.GA从许多点开始并行操作，在解空间进行高效启发式搜索，因而可以有效地防止搜索过程收敛于局部最优解；遗传算法在计算机上模拟生物的进化过程和基因的操作，通过目标函数来计算适配值，并不需要对象的特定知识，它具有全局寻优的能力，能解决高度复杂的问题，被广泛应用于自动控制、图形处理、电力调度等方面［1－5］.

调度系统所采用的数学模型对运行环境做了简化：车的速度恒定，保持匀速行驶，无特殊事件发生；以min作为最小的时间单位，这对安排时刻表是合理的；假设客流模型能反映该段线路上的日常客流量（假设到站乘客服从均匀分布，在不同时段有不同的分布密度）.

首班车发车时刻为早上6点整，末班车发车时刻为22点整，所有运营车都在整min时刻发车，1d之内的总班次为m，总时间为16h，即960 min.用xm表示第m辆运营车发车时刻距首发时刻的时间，以min为单位.决策变量为X＝［x1，x2，…，xn］T；染色体X 是一个完整的发车时刻表，其中的每个基因为一个车辆的发车时刻，约束条件为：

1）选择算子 采用比例选择法，也称为轮盘赌法.各个个体被选中的概率与其适应度的大小成正比.在一次选择中个体被选中概率为

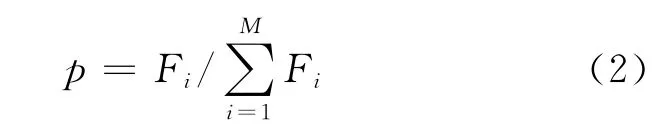
式中：Fi为该个体的适应度.

2）交叉算子 首先将群体中的M个个体以随机方式组成M／2对配对个体组，然后对每个个体组以概率P进行交叉运算，先在个体编码串中随机设置一个交叉点，然后在该点相互交换2个配对个体的部分染色体.交叉点的选择必须保证新的个体符合约束条件.

3）变异算子 采用均匀变异操作.依次指定个体编码串当中的个体基因座为变异点，对每个变异点以很小的变异概率p从对应基因的取值范围内取一个均匀分布的随机数来代替原来的基因.任一个基因xk的取值范围是（xk－1，xk＋1），变异点的新基因值为

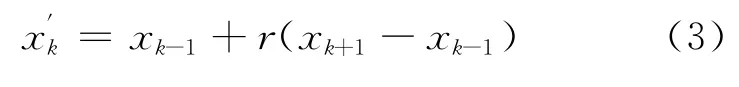
2 免疫机理引入遗传算法［6－7］

GA由于其运算简单和解决问题的有效能力而被广泛应用到众多领域.理论上已证明，遗传算法能从概率的意义上以随机的方式寻求到问题的最优解.GA在应用中也会出现一些问题，主要是容易产生早熟现象、局部寻优能力差等.一般来说基本遗传算法的求解效果往往不是最佳的；另外GA也无法避免多次搜索同一个可行解，这也是影响GA运行效率的一个因素.而有些寻优算法具有很强的局部搜索能力，可以预计在GA中融合这些优化算法的思想、构成一种混合遗传算法是提高GA运行效率和求解质量的一个有效手段.

免疫算法效仿生物免疫系统，把外来侵犯的抗原和免疫产生的抗体分别与实际求解问题的目标函数以及问题的解相对应，生成的抗体能有效地排除抗原，也就相当于求得了问题的最优解；对与抗原亲和力高的抗体进行记忆能促进快速求解.它具有以下特点.

1）抗体的多样性 通过细胞分裂和分化作用，免疫系统可产生多样性的抗体来抵御各种抗原.

2）自我调节能力.免疫系统具有维持免疫平衡的机制，通过对抗体的抑制和促进作用，能自我调节产生适当数量的必要的个体.要求免疫算法在进化过程中一旦发现最优个体，在兼顾群体多样性的同时，类似个体亦将大量繁殖.

免疫系统的算法是在个体基础上发展的；但物种宏观进化对个体免疫系统的进化是有重要影响的.免疫系统随着物种的进化一方面慢速进化，另一方面为了适应病原体环境而快速进化.它克服通常GA收敛方向无法控制的缺陷，收敛方向能得以控制.IGA可以看作是一种改进的遗传算法，一种新型计算智能方法，是具有免疫功能的遗传算法.它保留了遗传算法的全局搜索特性，克服遗传算法由于交叉搜索而在局部搜索解空间上效率较差的缺点，又在很大程度上避免未成熟收敛，许多方面表现超越遗传算法和免疫算法的优点.

3 IGA应用于公交静态调度

3.1 IGA的设计思想

IGA中的最优个体（抗体），即为每代适应度最高的可行解.从概率上来说，最优个体和全局最优解之间的空间距离可能要小于群体中其他个体与之的空间距离；和最优个体之间空间距离较小的个体也可能有较高的适应度，因此，最优个体是求解问题特征信息的直接体现.从免疫学的角度而言，当有抗原入侵时，与之相匹配的抗体被激发（免疫应答），使得有用的抗体一旦产生，就能得以保留.由上述分析可见，新算法成功与否的关键在于是否实施了精英保留策略以及是否充分利用每代最优个体信息.借鉴生物免疫机制，简单免疫进化算法中子代个体的生殖方式为

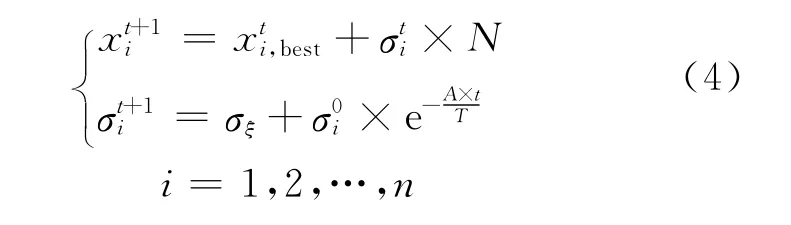
由式（4）式可得，一旦在某一代群体中确定出最优个体（抗体），那么在下一代群体中类似的个体（抗体），即为免疫应答在算法当中的体现.另外从进化角度而言，这里子代个体所表现出的性状不再仅仅视为是对父代个体突变的结果，而被视为是对父代性状遗传和变异的综合体现，IGA把子代个体这样的产生方式称之为生殖.

在IGA中，子代群体的分布是随迭代而不断进行有规律调整的过程，这是受生物免疫系统自我调节功能启发的结果.通过对标准差的动态调整，在进化的早期和中期，生成的群体在加大对最优个体附近解空间的投点密度的同时，也兼顾了对最优个体附近解空间以外区域的搜索，这样的群体既能保持较好的多样性，又可有效避免不成熟收敛这种现象；在进化后期，随着局部搜索能力的不断加强从而算法能以更高精度逼近全局最优解.所以标准差的动态调整是IGA的重要技术环节，可在群体多样性和选择力度之间起到调节的作用，相比与现有的其他进化算法而言，IGA中的群体只是起搜索引擎的作用，最优个体的进化是基于在一定概率规则引导下的一种统计结果.

综上所述，IGA算法的核心在于充分利用最优个体的信息，以最优个体的进化来代替群体的进化，通过标准差的调整把局部搜索和全局搜索在进化过程中有机结合起来.该算法的实现手段着重体现在最优个体的保留、生殖以及标准差的动态调整上，和现有其他算法相比，它具有搜索效率高和不易陷入局部最优解的优点.

3.2 IGA应用操作步骤

现仍采用上面建立的数学模型，初始规模N仍为200且不随进化代数而发生变化，便于IGA和GA比较.利用IGA来进行优化的步骤如下.

1）在解空间内随机生成初始群体，并计算其适应度，确定最优个体，并给出σ0的取值，A取为1，取为3，σξ取为0.

2）根据式（4）进行进化操作，在解空间内生成子代群体，规模为N.

4）重复执行步骤2）和3），直至达到终止条件，这里T取为100，选择最后一代的最优个体作为寻优的结果.

4 计算实例与分析

为了确定交叉概率、变异概率、进化代数等遗传算法参数，进行了许多实验，最终确定了效果较好的参数为：变异概率取0.000 5，交叉概率取为0.6.另外，群体规模取200，遗传代数取为600，这样可以兼顾运算量和运算效果.

图1分别画出了遗传算法和免疫遗传算法中各代个体目标平均值和各代最优个体目标平均值随进化代数的变化规律，从图中明显可以看出，IGA的收敛速度要优于GA，收敛更快.将IGA应用于公交智能调度管理系统能够得到较好的结果，可以迅速得到最优解.IGA是对GA的改进，从性能上也有了更大的进步.

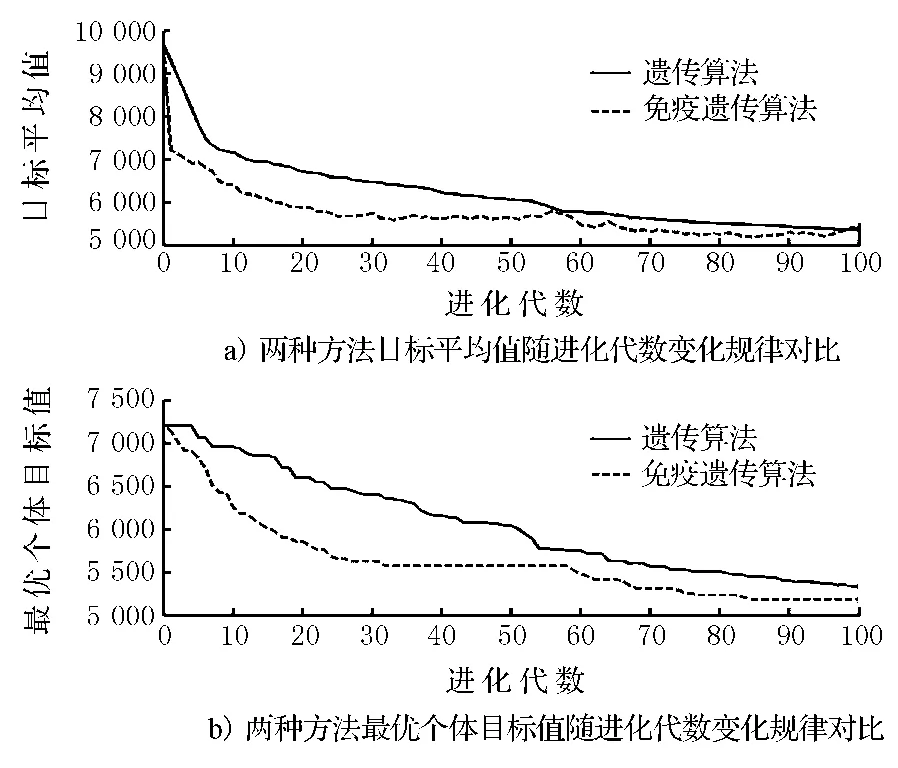
图1 遗传算法和免疫遗传算法应用对比

5 结 束 语

本文在遗传算法的基础上采用了一种较新的混合遗传算法－免疫遗传算法对公交静态调度进行了研究，并对二者的应用结果进行了仿真和比较，结果表明IGA有效的克服了简单GA的不足之处，并提高了寻优过程当中目标函数的收敛速度，并得到了合理的发车时刻表，可以提高公交企业的服务水平，对改善城市交通问题和节约市民出行时间有实际意义.由于公交车在运行过程中受到诸多客观因素的影响，比如车辆可能没有按计划到达预定车站，在车辆运行的过程中要对公交车运行的实际情况进行实时调度，因此还需要对动态调度做进一步的研究.

［1］倪长健.免疫进化算法研究及其在水问题中的应用［D］.成都：四川大学水电学院，2003.

［2］周 明，孙树栋.遗传算法原理及应用［M］.北京：国防工业出版社，1999.

［3］李跃鹏，安 涛.基于遗传算法的公交车辆智能排班研究［J］.交通运输系统工程与信息，2003，3（1）：41－45.

［4］王小平，曹立明.遗传算法理论应用与软件实现［M］.西安：西安交通大学出版社，2002.

［5］Marian T B.Development of a transportation data processing system for Metropolitan［C］／／Proceedings of the IEEE－IEE Vehicle Navigation and Information Systems Conference，1993：186－190.

［6］Malmborg C J.A genetic algorithm for service level based vchicle scheduling［J］.European Journal of Operational Research，1996，93：121－134.

［7］De Jong K A.An analysis of the behavior of a class of genetic adaptive［D］.Ph.D Dissertation，University of Michigan，1975.