基于脉冲控制的不确定混沌系统的同步

胡爱花，吴昌应

（1.江南大学理学院，江苏无锡214122；2.无锡市文化广电新闻出版局广播电视处，江苏无锡214001）

0 前言

近年来，混沌同步的应用从物理学迅速扩展到了生物学、信息科学和保密通信等领域［1－3］。由于混沌同步在工程技术上的重要价值和较广阔的应用前景，它一直是非线性科学领域的研究热点之一。混沌同步主要有4类［4］：完全同步、相同步、滞后同步以及广义同步。其中，完全同步是最基本的同步形式。所谓完全同步，是指两个相同混沌系统的相轨迹随时间渐近地趋于一致。由于混沌系统对初始值的敏感依赖性，两个初始值不同的混沌系统很难达到完全同步。目前，研究者们已经提出了各种各样的方法来控制混沌系统从而实现完全同步［5－7］。

然而，在实际环境中，混沌系统的参数往往会由于受到外界因素（如噪声、温度等）的干扰而在一定范围内发生波动，这样就使得原先确定的混沌系统变得不确定。这些外界因素基本上不可避免，因此，研究不确定混沌系统的同步更具有现实意义。针对这一问题，已经取得了一些成果，例如文献［8－9］，提出可以利用滑模控制方法和自适应控制方法。

本文将应用脉冲控制方法来研究两个不确定混沌系统的完全同步化，和其他方法相比，该方法的优点在于脉冲时间离散，脉冲强度小，因此控制所需的代价小。脉冲控制方法的数学模型是脉冲微分方程，描述的是在某些时刻以跳跃形式改变其状态的演化过程。两个混沌系统的脉冲同步问题可以转化为同步误差系统零点的稳定性问题。本文研究的主要内容是：考虑驱动系统和响应系统的参数发生扰动，并且假定系统本身和扰动满足一定的条件，采用脉冲控制方法控制响应系统，从而使驱动系统和响应系统达到完全同步状态。文中推导出了脉冲控制所需要的脉冲强度与间隔，给出了严格的理论证明，同时以具体的数值例子加以了验证。

1 脉冲微分方程的基本理论

考虑一个脉冲时刻固定的脉冲微分系统：

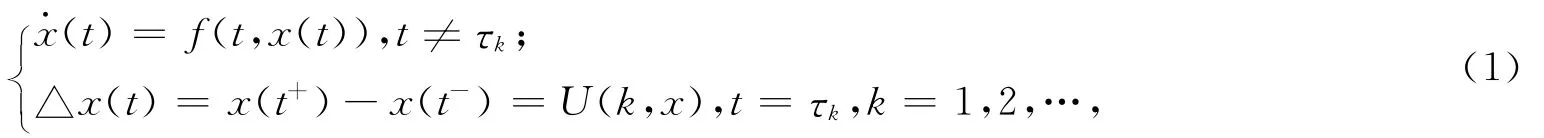
其中：f：R＋×Rn→Rn；U：Rn×Rn→Rn是连续的；x∈Rn表示状态向量；0≺τ1≺τ2≺…≺τk≺τk＋1≺…，当k→∞时，τk→∞。

为方便推导，类似于文献［10］，给出如下定义：

定义1 令V：R＋×Rn→R＋，若以下条件满足，则称V属于类V0：

（1）V在（τk－1，τk］×Rn上连续，并且对于任意x∈Rn，k＝1，2，…（t，y）＝V（τ，x）存在；

（2）V对于x满足局部Lipschitz条件。

定义2 对于（t，x）∈（τk－1，τk）×Rn定义：

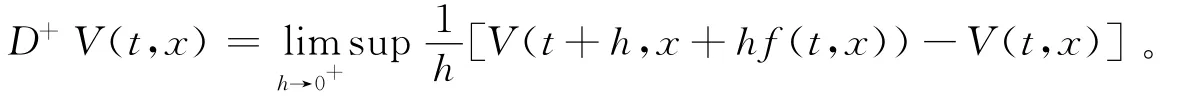
定义3 比较系统，若V∈V0且满足如下条件：

其中g：R＋×R＋→R连续；Ψk：R＋→R＋是不减函数；那么称下式为系统（1）的比较系统：

2 不确定混沌系统的同步化

考虑如下不确定混沌驱动系统：

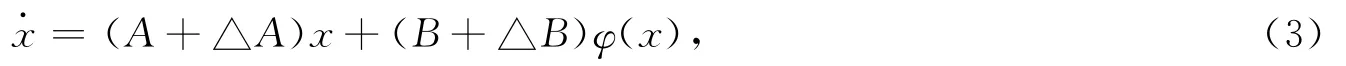
其中：x∈Rn是状态向量；A、B∈Rn×n代表系统的参数矩阵；φ是非线性向量函数；△A和△Β为不确定项。本文中定义：

其中：H1、H2∈Rn×1，E1、E2∈R1×n，它们都代表扰动强度；F（t）是外界不确定因素，如噪声。

受脉冲控制的响应系统可表示为：

其中：C∈Rn×n是脉冲强度；τi（i＝1，2，…）满足：0≺τ1≺τ2≺…≺τi≺τi＋1≺…→∞。

令同步误差向量为e＝［e1，e2，…，en］T＝x－y。由式（3）和式（6）可得误差系统如下：

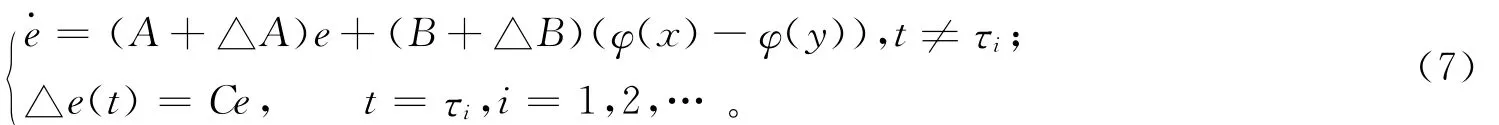
在推导同步化条件之前，需要作如下假设并引入相关引理。

假设1 函数φ满足全局Lipschitz条件：

其中L是一个正常数。

假设2 在假设1满足的前提下，矩阵B满足：

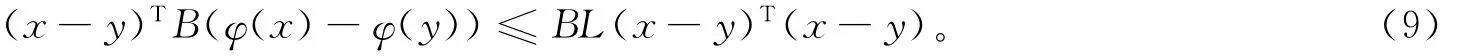
假设3 不失一般性，假设 F（t）≤1。

引理1［11］若X和Y是适当维数的向量或矩阵，那么对于任意正常数α，以下不等式成立：

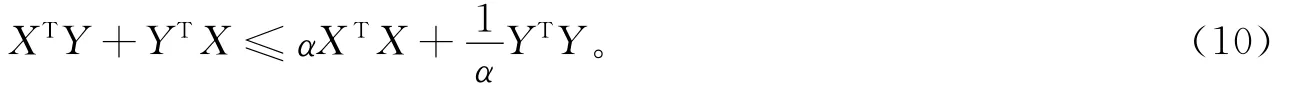
经过推导，给出系统（3）和（6）的同步化条件，如下：

定理1 驱动系统（3）和响应系统（6）将实现完全同步化，若存在常数ξ≻1和一个当t≠τk时可导的不增函数K（t），满足：

其中：λ1＝λmax（A＋AT），λ2＝Lλmax（B＋BT），λ3＝（EE1），λ4＝ε1λmax（H1H），λ5＝（EE2），λ6＝Lε2λmax（H2H），λmax（A）代表矩阵A的最大特征根；ε1、ε2≻0是任意正常数；d＝ ρ2（I＋C），ρ（A）表示矩阵A的谱半径；｛τi：i＝1，2，…｝是变化的，满足：

且对于任意给定的常数ε，下式成立：

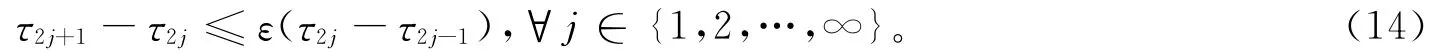
证明 选取Lyapunov函数为V（t，e）＝eTe。

当t≠τi，沿着误差系统（7）的解轨线，得：

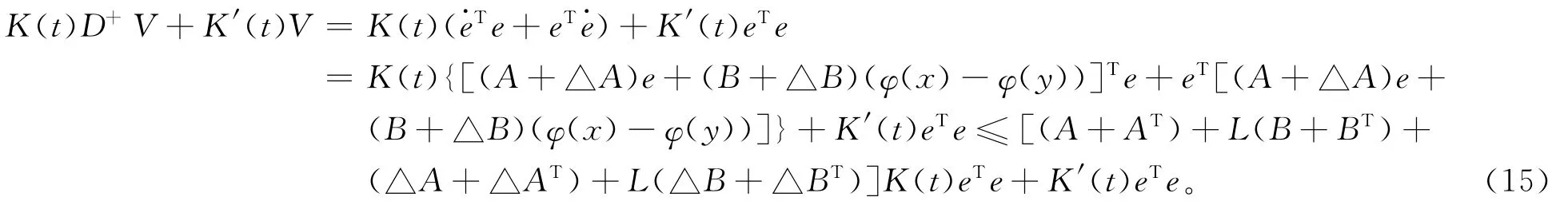
根据引理1，得到对于ε1、ε2≻0，有：

因此，可简化不等式（15）为：

当t＝τi，沿着误差系统（7）的解轨线，得：

由文献［12］可知系统（7）的渐近稳定性可由如下比较系统来判定：

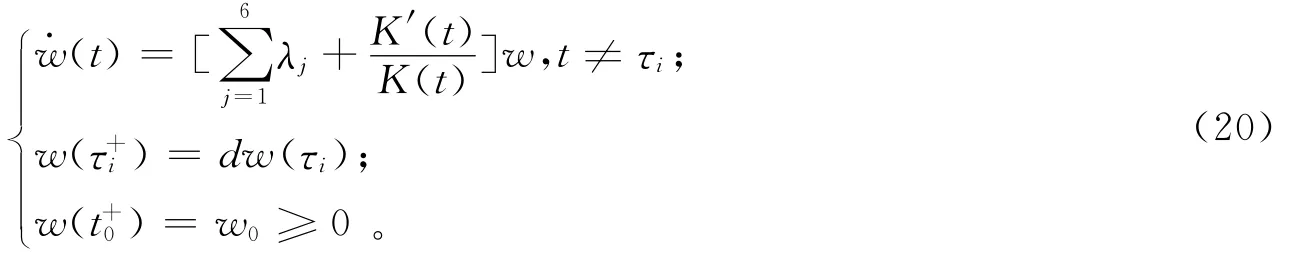
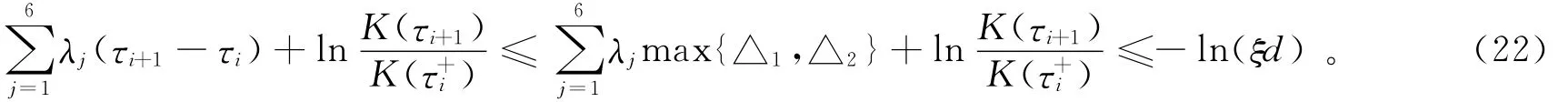
其中，上述不等式（21）和（22）可分别从式（11）和（12）推导得出；因此由文献［12］可知系统（7）的平凡解将渐近稳定。定理1得证。

注1 通过定理1，可估计出脉冲间隔△2的上界△2和△′2：

3 数值仿真

以Chua's电路［13］为例进行仿真，如下：

其中：α≻0；β≻0；a≺b≺0；φ定义为：

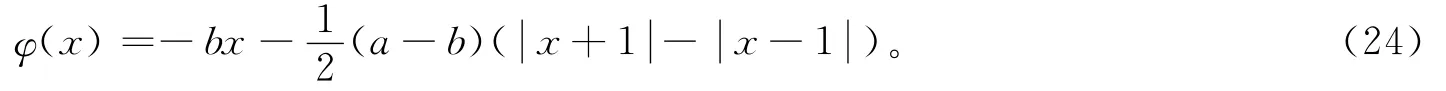
由此可得：

假设1成立。

当α＝10.0，β＝14.87，a＝－1.27，b＝－0.68，Chua's电路有双卷波混沌吸引子，如图1所示。

根据式（3）和式（6），得到：

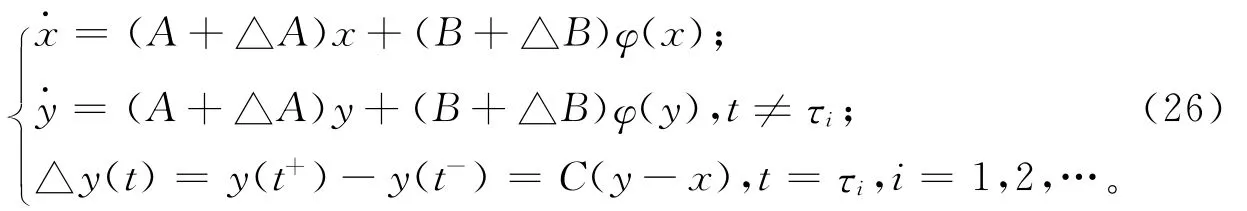
其中：x＝［x1，x2，x3］T；y＝［y1，y2，y3］T；

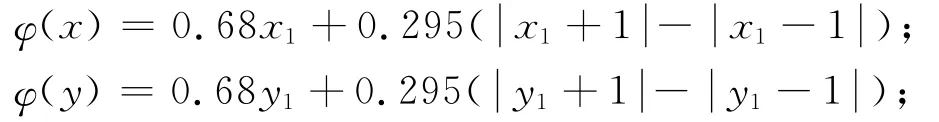
图1 Chua's电路三维图

假设H1＝H2＝＝［1 1 0］，E2＝［1 0 0］，F（t）＝0.1sin（t）＋0.1cos（t）。可得：

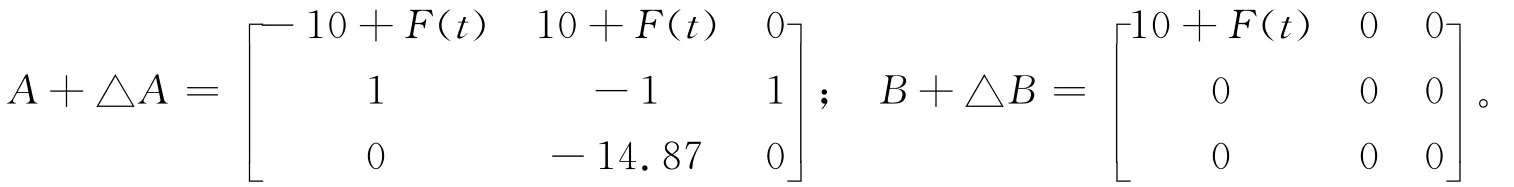
可以看出，系统参数α受到外界因素F（t）的影响。

选取x（0）＝（0.1，0.1，0.1），y（0）＝（0.2，0.2，0.2），x（0）和y（0）分别代表驱动—响应系统的初值；

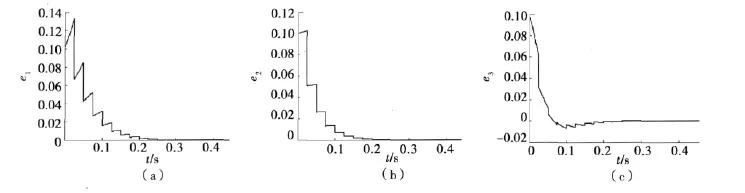
图2 驱动－响应系统的误差e i（i＝1，2，3，e i＝x i－y i）

从图2中可以看出：误差ei很快地趋于0，表明驱动—响应系统较好地实现了同步。

4 结论

本文研究了基于脉冲控制的两个不确定混沌系统的完全同步化问题。所采用的控制方法具有变化的脉冲间隔，同时还估计出了脉冲间隔的上界。从仿真中可以发现，控制过程中所需的脉冲强度小，同步速度较快，同步效果较好。理论分析结果不仅适用于Chua's电路，同样适用于满足假设条件的其他混沌系统。

［1］ Jiang N，Pan W，Yan L，et al.Two Chaos Synchronization Schemes and Public－Channel Message Transmission in a Mutually Coupled Semiconductor Lasers System［J］.Opt Commun，2009，282（11）：2217－2222.

［2］ Jovic B，Unsworth C P，Sandhu G S，et al.A Robust Sequence Synchronization Unit for Multi－user DS－CDMA Chaosbased Communication Systems［J］.Sig Proc，2007，87（7）：1692－1708.

［3］ Zhou J，Huang H B，Qi G X，et al.Communication with Spatial Periodic Chaos Synchronization［J］.Phys Lett A，2005，335（2／3）：191－196.

［4］ Brown R，Kocarev L A.Unifying Definition of Synchronization for Dynamical Systems［J］.Chaos，2000，10（2）：344－349.

［5］ Wu X，Chen G，Cai J.Chaos Synchronization of the Master－slave Generalized Loren Systems Via Linear State Error Feedback Control［J］.Phys D，2007，229（1）：52－80.

［6］ Chen H，Sheu G，Lin Y，et al.Chaos Synchronization Between Two Different Chaotic Systems Via Nonlinear Feedback Control［J］.Nonlinear Anal，2009，70（12）：4393－4401.

［7］ Tang R，Liu Y，Xue J.An Extended Active Control for Chaos Synchronization［J］.Phys Lett A，2009，373（16）：1449－1454.

［8］ Ablay G.Sliding Mode Control of Uncertain Unified Chaotic Systems［J］.Nonlinear Anal，2009，3（4）：531－535.

［9］ Zhou J，Er M J.Adaptive Output Control of a Class of Uncertain Chaotic Systems［J］.Sys Contr Lett，2007，56（6）：452－460.

［10］Lakshmikantham V，Bainov D D，Simeonov P S.Theory of Impulsive Differential Equations［M］.Singapore：World Scientific，1989.

［11］Wang Y Y，Xie L H，Souza C E.Robust Control of a Class of Uncertain Nonlinear Systems［J］.Syst Contr Lett，1992，19（2）：139－149.

［12］Sun J T，Zhang X P，Wu Q D.Less Conservative Conditions for Asymptotic Stability of Impulsive Control Systems［J］.IEEE Trans Autom Control，2003，48（5）：829－831.

［13］ Shil'nikov L P.Chua's Circuit：Rigorous Results and Future Problems［J］.Int J Bifurcat Chaos，1997，7（3）：665－669.