聚四氟乙烯复合材料摩擦学性能的人工神经网络研究

史以俊， 罗振扬， 何 明， 顾晓利

(南京林业大学理学院，江苏南京 210037)

聚四氟乙烯(Poly tetrafluoroethylene，简称PTFE)有着优异的耐腐蚀及自润滑性能，广泛用于石化、航空航天及电子等领域，但其耐磨性差且易蠕变，在实际使用过程中通常需要加入填充材料[1]。研究表明，不同尺寸、形状的填料协同增强，可以大大提高PTFE的性能[2，3]。然而，目前已有的预测手段只能简单粗略地预测单一填料填充PTFE复合材料的摩擦磨损性能[4，5]，不能适用于多元填充体系复合材料性能的预测。

为了研究人工神经网络(A rtificial Neural Network，简称ANN)对多元增强PTFE复合材料摩擦磨损性能的预测，本文以碳纤维(CF)及颗粒氧化硅(SiO2-P)混杂增强的PTFE复合材料为例，建立了材料组成、测试条件与其摩擦学性能之间的网络模型。

本文对比了ANN算法种类以及不同网络结构对预测结果的影响，在此基础上利用已有实验数据对ANN进行训练，并最终对CF及SiO2-P协同增强PTFE复合材料的摩擦磨损性能进行预测及验证。

1 PTFE复合材料性能测试

(1)原料及PTFE复合材料的制备。PTFE:平均粒径25μm，杜邦公司;CF:平均直径15μm，平均长度90μm，市购;SiO2-P:平均粒径1μm，市购。将质量分数为0～12%的SiO2-P和0～25%的CF加到PTFE粉末中，机械搅拌混合均匀，冷压成型，再经程序控温烧结制备不同的试验样品。加工后的样品和对偶材料(45#钢)在试验前用800号金相砂纸打磨到R a=0.2μm，丙酮清洗干燥。

(2)摩擦磨损性能测试。利用MPX-2000型磨损试验机双环形式(河北宣化)，考察不同试验条件下，PTFE复合材料的摩擦磨损性能。试验条件:室温的相对湿度为50%～55%，载荷为100、200、300、400 N，滑动速度为0.467、0.692、1.4m/s，试验周期60m in。对偶件为45#钢，材料和对偶件在试验前用800目金相砂纸打磨。正式摩擦测试前，先进行5 min磨合。试样在测试前后清洗去屑，放入烘箱105℃干燥3 h。磨损失重用精度为0.1 mg电子天平称量，磨损量由磨损失重计算而得，摩擦系数由电脑在线采集摩擦力矩经计算转换获得，取后45 m in内平均值。

2 ANN模型的建立及优化

(1)ANN的建立。本文利用M atlab6.5软件中的神经网络工具箱[6]，选用材料组成及测试条件作为输入变量，以摩擦系数或磨损量为输出量建立ANN模型，具体数值见表1所列。输入层与隐层间的传递函数采用tansig函数，隐层与输出层间的传递函数采用purelin函数，取误差指标为0.000 1，最大迭代歩数为105。

表1 人工神经网络的输入输出参数

计算时，实验数据被分为2个部分，用于训练和检验网络的优劣。训练数据用于修订神经元之间连接的权重，直至达到设定的最小误差或最大迭代步数;然后用检验数据计算预测值与实验值的平均误差，进而判断选定网络的优劣，这2组数据均从实验数据中随机抽取。对于每个网络，本文均进行多次训练、检验，重复次数为30。

(2)ANN的优化。ANN有很多学习算法可用来优化网络计算，一般来说不同的算法适合于不同的问题。本文对比了批梯度下降算法(GD)、动量批梯度下降算法(GDM)、自适应修改学习率算法(GDA)、有弹回的神经网络算法(RP)、共轭梯度算法(SCG)及高斯-牛顿算法(OSS)这6种ANN算法的优劣。

对比ANN算法的优劣时，本文选用5-[50]1-1网络结构，该结构具有一层隐含层单元，隐含层神经元个数为50，以3种材料组成及2种测试条件作为输入层的5个神经元输入量，以数据离散更为明显的磨损量作为输出层神经元的输出量。从实验数据中随机选取70组数据作为训练数据，30组作为检验数据。在这里需要指出的是，本文共测得相关实验数据120组，由于篇幅限制，未在正文中列出具体实验数值。

图1所示给出了不同算法的平均误差R的结果，从中可以看出SCG算法的R值较其它几种算法的要小，因此本文选用SCG作为ANN的学习算法。

图1 各种ANN学习算法的平均误差比较

除了学习算法外，ANN的网络结构也会较大程度地影响其运算结果。根据Kolm ogorov理论，至多使用4层隐含层结构就可以解决一切实际问题[7，8]。

因此，本文采用SCG算法对比了具有1～4层隐含层单元共8种ANN网络结构的误差大小，训练、检验过程同上。图2所示给出了使用不同网络时的误差数据，从中可以看出，采用网络结构5-[15∶10∶5]3-1时的误差值要比采用其它几种网络时的误差值低。文献[8]认为，对于大多数实际问题，2层隐含层就足以获得较好的学习结果。但是本文研究发现对于复合材料的摩擦磨损问题，具有3层隐含层的网络结构更加有利于关联输入条件及输出结果。

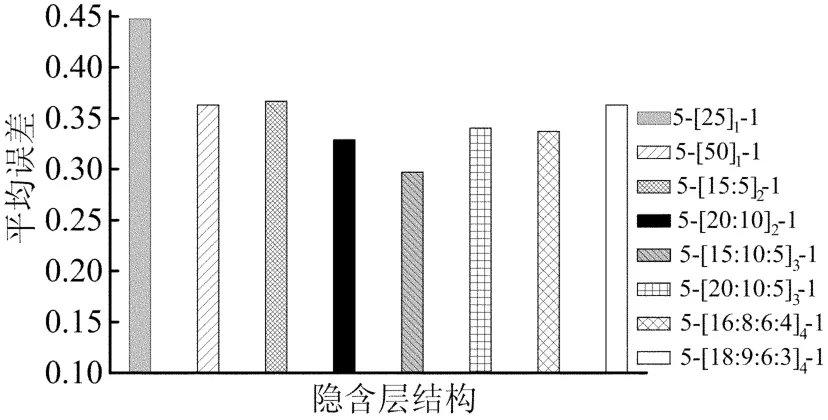
图2 不同ANN隐含层结构平均误差的比较

3 ANN模型预测及分析

本文选用已有的实验数据对神经网络进行训练，学习算法采用SCG算法，神经元结构为5-[15∶10∶5]3-1，训练结束后输入想要预测的输入条件即可获得预测结果。

图3所示给出了200 N、0.692 m/s条件下，ANN对PTFE复合材料摩擦磨损性能的预测。对于预测结果，本文对比了5种不同组成PTFE复合材料的实验值与预测值之间的误差，在图3中用差值线表示。

图3 PTFE复合材料的摩擦系数及磨损量预测结果

由图3可以看出，各点摩擦系数及磨损量的预测值与实验值间的误差均小于10%。

4 结 论

(1)同其它几种常用的人工神经网络算法相比，共轭梯度算法(SCG算法)更适合用于PTFE复合材料摩擦磨损性能的预测。

(2)对于复合材料的摩擦磨损问题，具有3层隐含层的网络结构更有利于关联输入条件及输出结果。本文研究表明，采用5-[15∶10∶5]3-1的网络结构时，ANN有最佳的预测效果。

(3)样本检验表明，采用SCG算法、5-[15∶10∶5]3-1网络结构的网络模型对磨损量和摩擦系数的预测具有较高的精度，数据预测值与试验值误差在10%以内。

ANN预测同时还得到200 N、0.692m/s测试条件下，PTFE复合材料的最佳耐磨配方为15CF+6SiO2-P，重新进行实验验证发现，其与实验值的误差仅为7%。

[1] Shi Yijun，Feng X in，W ang Huaiyuan，et al.Effectsof filler crystal structure and shape on the tribological properties of PTFE composites[J].Tribology International，2007，40:1195-1203.

[2] Shi Yijun，Feng Xin，Wang Huaiyuan，et al.Tribological and mechanical properties of PTFE composites filled with the combination of short carbon fiber and carbon nano-fiber[J].Key Engineering Materials，2007，334/335:689-692.

[3] 汪怀远，冯 新，史以俊，等.纳米TiO2与炭纤维协同填充PTFE复合材料的摩擦磨损性能[J].高分子材料科学与工程，2007，23(4):89-93.

[4] Bahadur S，Gong D.Formulation of themodel for optimal proportion of filler in polymer for abrasive w ear resistance[J].W ear，1992，157:229-243.

[5] Jiang Z，Zhang Z，Friedrich K.Prediction on wear properties of polymer composites with artificial neural netw ork s[J].Composites Science and Technology，2007，67:168-176.

[6] 张志通.精通Matlab[M].北京:北京航空航天大学出版社，2006:60-80.

[7] Ku rkova V.Kolmogrov's theorem is relevant[J].Neural Com putation，1991，3(4):617-622.

[8] Hornik K，Stinchocombe M，W hite H.M ultiplayer feedforw ard netw orks are universal approximators[J].Neural Netw orks，1989，2:359-366.