公路斜交板桥的设计及交角的影响

张建成

(石家庄市公路桥梁建设集团第五公路工程处)

0 概 述

随着现代交通的发展,公路斜交桥越来越多,这是因为它最容易满足各种线型要求。无论是跨越斜交河流、通道,还是位于纵横坡或超高段,斜交桥都能做的顺适得体。斜交桥的几何形状具有很好的可塑性。

在 20世纪六、七十年代,人们尽量避免斜交桥,或者硬性把桥扭成正交,或者改变路线走向,正交过河。这除了施工放养较为复杂外,和斜交桥的受力不明确也不无关系。目前对斜交桥仍采用经验的、近似的办法进行计算。计算结果不像正交桥那样令人放心。在桥梁检查时,对斜交板这样那样的裂缝,要做出准确的原因分析和对策,往往是很困难的。

在斜交板设计中,各国都有各自的设计方法。目前,已积累了大量的实例资料,并开始采用有限元分析,概括介绍如下。

1 中国规范的计算方法

关于跨长、板宽及斜交角的定义当斜桥为现浇板时,我们认为他是整体式板。

当交角 φ＜15°时,可按正交板计算,但所取计算跨长还要按跨宽比(1/b)而定:当板宽较宽时(1/b≤1.3),取盖梁间的垂直距离L1为计算跨经;当板宽较窄时(1/b＞1.3)时,取斜跨 L为计算跨径。

在工程实践中经常会遇到 φ＞15°的情况,现行规范未明确指定计算方法。“规范说明”中参考了奥尔森的试验结果:

(1)跨宽比l/b≥1.3时,只要φ≤40°,均按正交桥计算,计算跨径取斜跨;

(2)跨宽比l/b=1.3～0.7时,当φ＜15°时按正交计算,计算跨径取正跨;当 15°＜φ＜40°时计算跨径取1/2(斜跨+正跨);

(3)跨宽比l/b＜0.7时,只要φ≤40°,一律按正交设计,计算跨径取正跨。

当斜交桥为预制板时,我们认为板间连接只传递剪力,内力计算时视一块板为一个受力单元,按单向板计算。

2 美国规范(AASHTO)的计算方法

建议,当斜交角小于 30°时,斜交板可以按同跨度的正交板计算而不加修正;当斜交角大于 30°时,需用其他计算格式进行计算。

该规范首先把车轮荷载进行横向分布,然后把整体板分成若干条小梁进行分析。这样就把双向弯曲问题简化成了单向弯曲问题。先求出一个车道内的弯矩和剪力,再除以车道宽度,便可以求出单位宽度板内的弯矩和剪力。

另外还有一种简单的算法:斜交板的内力等于正交板的内力乘以折减系数,该系数γ≤1.0。即

式中:φ为斜交角,通过试算可知,当 φ＜12°时,γ=1.0,可以不进行修正。

3 FEA计算方法和试验结果

利用SAP2000程序,进行三维有限元分析(FEA),是一种精确的计算方法。所取变量有跨长、板宽和斜交角。计算结果表明,AASHTO方法大部分情况都偏于保守,尤其是偏角很大时,它过高的估算了纵向最大弯矩。

斜交桥与正交桥比较:设定Mφ为斜跨桥弯矩,M0为正交桥弯矩,则 Mφ/M0随着斜交角度的增大而减小。在 φ＜20°时,Mφ/M0≈1.0;当φ为30°～40°时,Mφ/M0=0.75;当φ达到 50°时,该比值可达0.5,即斜桥弯矩只有正桥弯矩的一半。与这一趋势相似的是斜板的活载挠度:斜交角φ为20°时,挠度比正交桥下降 10%;φ为 30°时,下降 25%;φ为40°～50°时,挠度可下降 40%。

4 斜板的配筋

顺桥轴方向的纵向钢筋,按计算出的弯矩进行配置。板的自由边缘带可认为是一片“边梁”(约为 0.5m),通常要多配一些钢筋,一般不少于3根。斜交板的交角在15°以下时,主筋的方向和正交一样,即沿着桥梁纵轴线方向配置;但取正跨为计算跨径时,主筋应沿着正桥方向布置,通常当φ＞15°时应按正桥方向布置。

特别应该注意的是,钝角部位受力复杂,应配置加强钢筋:顶层加强钢筋方向应垂直于钝角平分线;底层加强筋应平行于钝角平分线;钢筋直径不小于 12mm,间距 10～15cm。

与正交桥不同,斜交桥的横向钢筋不单单是起分布作用,它还有承受弯矩的功能。随着斜角度的增大,横向弯矩也在增大,所以顺时的横向钢筋应按受力筋考虑。配置数量可按纵向主筋的百分比控制,百分比n可按下式计算

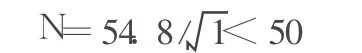
式中:L为跨径,m;n值不超过50%。如L=9m时,n= 54.8=18,即横向配筋率应为纵向主筋的 18%。

5 结 论

(1)当斜交角度不大于 20°时,按有限元法和按规范求得的最大纵向弯矩基本相同。

(2)当交角增大时,美国AASHTO规范过大的估算了最大弯矩:当 φ为 30°时,多算了 20%;当 φ为 40°时,多算了50%;当φ达到 50°时,多算了 100%。

(3)斜交桥与正交板相比:设斜交桥弯矩与正交桥弯矩之比为n。当交角为 20°时,n=1.0;当交角为 30°～40°时, n=0.75;当交角增至50°时,n=0.5。

(4)当斜桥的纵向弯矩减小时,横向弯矩却在增大。

(5)随着交角的增加,最大活载挠度在减小,趋势与纵向弯矩相似。当交角大到40°～50°时,挠度可减小到正交桥的0.6。

(6)一般认为,斜角角度不大于 20°时,可按正交桥计算,当交角大于 20°时,应按三维有限元法进行分析。