基于IGA算法优化的RBF神经网络应用

张文广，徐宇茹，姜 鹏，史贤俊

（1.海军航空工程学院 a.控制工程系；b.训练部，山东 烟台 264001；2.91065 部队，辽宁 葫芦岛 125001）

径向基函数（Radial Basis Function，RBF）网络是一种性能优良的三层前馈式神经网络，具有以任意精度逼近任意连续函数的能力，并被广泛应用于众多领域[1]。与传统的BP网络相比，径向基函数网络（RBFNN）是局部逼近网络，具有学习速度快，不存在局部极小的优点，同时具有很强的函数逼近和模式分类的能力。目前用于径向基函数网络学习算法主要有无监督的聚类方法、监督学习方法及与回归有关的正交二乘回归方法（Orthogonal Least Square Regression，OLSR）、偏最小二乘回归方法（Partial Least Square Regression，PLSR）等。聚类方法存在类别数须预先指定，且类别数的选取又会影响聚类性能等不足；监督学习方法本质上与误差反传算法相同，与初值有关，且难以找到全局最优；正交二乘回归与偏最小二乘回归方法都较好地解决了隐单元数和各中心的取值问题，但在选定宽度系数和回归参数时，需用尝试与交叉验证方法，存在很大的局限性。

遗传算法是模拟生物在自然环境中的遗传和进化过程而形成的一种自适应全局优化搜索算法。它是解决函数优化问题、模式识别问题、神经网络的参数调整和优化等问题最有效的方法之一[2-4]。

针对传统BP网络以及简单遗传算法的不足，本文提出了一种基于改进遗传算法（Improved Genetic Algorithm，IGA）的RBF神经网络，该网络引入自适应机制的实数编码的遗传算法，从初始群体生成及遗传算子操作等方面作了改进，并将其与梯度下降法混合交互运算，作为径向基函数网络的学习算法，应用于非线性函数的逼近和导弹故障模式的识别问题。仿真结果表明，基于IGA算法的RBF网络不仅结构简单，而且具有较好的网络泛化性能。

1 径向基函数网络设计

1.1 RBF网络的结构

径向基函数网络[5]是局部逼近网络，一般由3层组成（n个输入、m个隐节点、p个输出），其结构如图1所示。

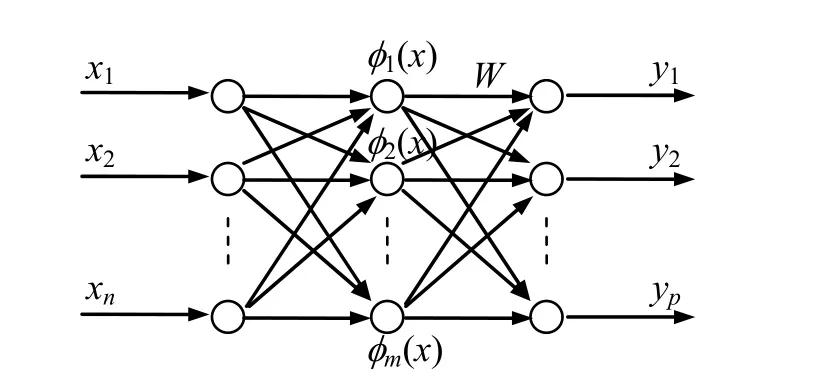
图1 径向高斯函数网络拓扑结构

RBF网络基函数常用的是高斯函数，可表示为

式中：φi(x)为第i个隐层节点的输出；X为输入样本，ci为第i个隐层节点的高斯核函数的中心且与X 具有相同的维数；iσ为第i个隐层节点的变量，称标准化常数或基宽度。

RBF网络的输出为隐层节点输出的线性组合，有

1.2 网络参数的学习算法

这里采用梯度下降法来学习RBF网络的中心ci和宽度参数 σi。为讨论方便，考虑输出层只有一个节点的情况，将式(1)代入式(2)中得到

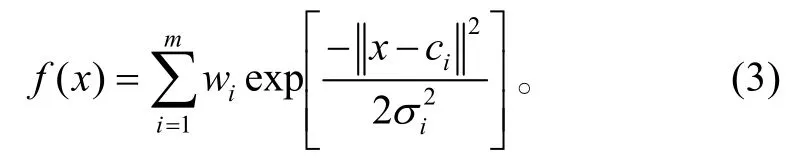
设网络的期望输出为yd(x)，网络的能量函数：

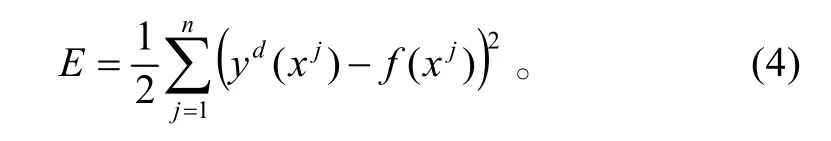
将 f (xj)代入式(4)，得到

设样本数为L，则

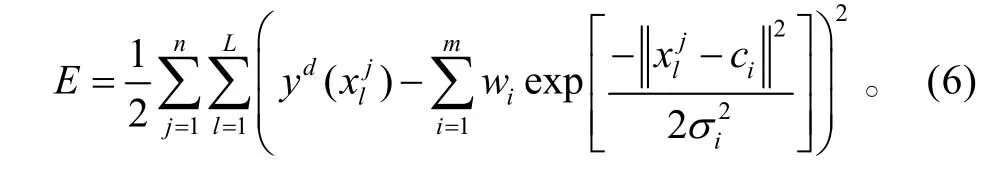
记

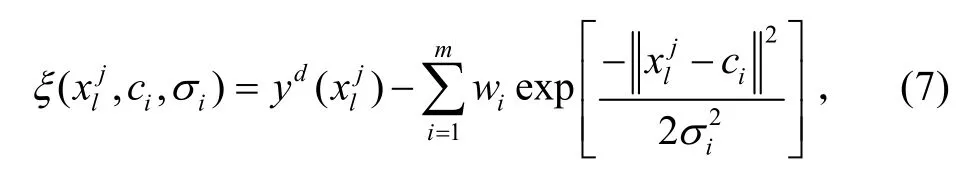
则式(6)变为

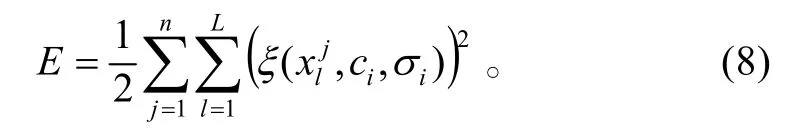
在学习中心值和宽度参数时，认为iw为常数，则可得中心值和宽度参数更新公式为

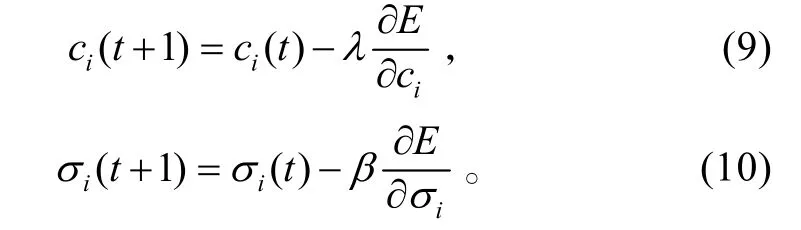
式(9)、(10)中，λ、β分别为中心值和宽度参数的学习效率。将式(8)分别代入式(9)和式(10)，经整理得

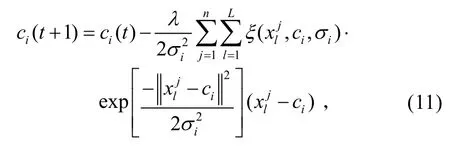
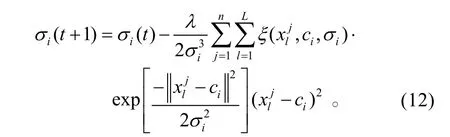
依据输入样本，利用系统辨识理论中的最小二乘算法可求出输出层的权值。本文采用的隐层和输出层之间的联接权的学习算法为

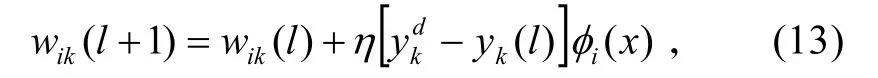
2 基于改进遗传算法的RBF网络训练

RBF网络设计的核心问题是确定隐节点数目和基函数的中心值和其他参数，设计出满足目标误差要求的尽可能小的神经网络，以保证神经网络的泛化能力。

2.1 编码方式和适应度函数的确定

为克服二进制编码的不足，本文对遗传算法采用实数编码方式，即把RBF网络的隐层节点数m、每一隐节点的中心参数 ci和宽度参数 iσ 编成染色体，把网络中这些参数的集合看成一个个体，并在初始化阶段采用完全随机方式产生初始群体。群体规模影响遗传优化的最终结果以及遗传算法的执行效率。一般地，群体规模取为50～200 较好。

遗传算法中适应度函数的选取至关重要，下面构造能量函数E，使其最小值对应于问题的最优解：

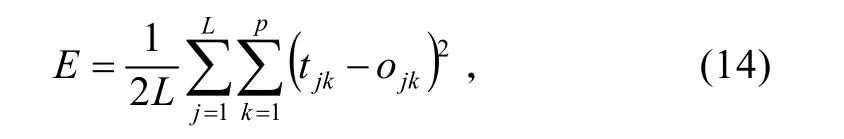
式中：tjk为第k神经元关于第j个样本的期望输出；ojk为第k神经元关于第j个样本的RBF网络输出。

于是，适应度函数可由下式构造：

2.2 初始种群的产生

为改善初始种群的性质，本文采用了一种所谓的小区间生成法[6]。该法是先把各待优化参数的取值范围分成种群总数个小区间，再在各小区间中分别随机生成一个初始个体。这样生成的初始个体将会均匀地分布在整个解空间上，并能保证随机产生的各个体间有明显的差距，保证了初始种群含有较丰富的模式，增强了搜索收敛于全局最优点的可能。

2.3 复制与选择操作

为了保证搜索到的最佳个体不会被各种遗传操作破坏，并保留上代群体的优良特性，本算法将上代群体全部复制保留到匹配池中。

对于匹配池中的个体，采用如下两种方式进行选择以产生子代群体：

1）实施最优保留策略：将匹配池中适应度值最大的个体无遗传变化地放入子代群体，以保留上代群体的最优解，使算法可以以概率1 收敛于全局最优解，保证了算法的收敛性；

2）两两竞争选择策略：对匹配池中除最优解以外的其他个体进行两两竞争选择，从匹配池中随机选取两个个体，比较它们的适应值，把适应值较大的个体保留到子代，直到产生完整子代群体。

2.4 自适应交叉操作

交叉采用实数编码遗传算法中的实值中间重组法[7]，遗传算法中交叉概率cP的选择对算法行为和性能都有着重要影响，为保证交叉的质量，交叉概率采用自适应方式产生，即交叉概率由进化程度控制。则改进的自适应交叉概率[8]由下式确定：

式中：fmax为群体中最大的适应度值；favg为每代群体的平均适应度值；f′为要交叉的两个个体中较大的适应度值。这里，可取Pc1=0.9，Pc2=0.6。

2.5 非均匀自适应变异操作

变异是对优选交叉后的个体进行的。为保证能搜索到解空间中的每一点，使算法具有全局收敛性，这里采用实数编码的非均匀变异（Non-uniform Mutation）方式。

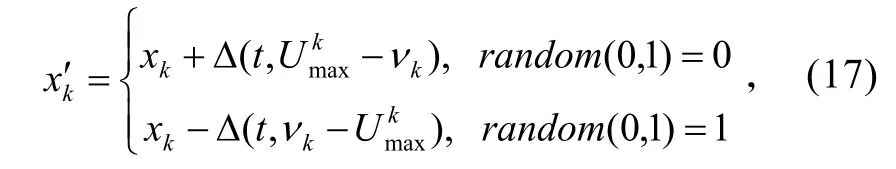
式中，∆(t,y)为在[0,y]范围内符合非均匀分布的随机数。∆(t,y)表达式为：

式中：t为群体进化的代数；r为[0,1]间符合均匀分布的随机数；T为最大进化代数；b为系统参数（一般取值为2）。

同样，为了保证变异的质量，这里采用改进后的自适应变异概率，其具体表达式为：

式中：fmax为群体中最大的适应度值；favg为每代群体的平均适应度值；f为要变异个体的适应度值。这里，可取Pm1=0.1，Pm2=0.001。

2.6 算法实现

将RBF网络结构优化和参数学习分两个阶段进行，即训练和进化。首先，随机生成N个个体，组成群体，用梯度下降法学习每一个体中的隐节点数染色体对应的网络中的中心 ci和宽度参数iσ，用最小二乘法学习网络的线性权值iw；其次，用遗传进化算法优化隐节点数，通过这两个过程的交替进行，得到隐节点数最小满足误差要求的基函数且具有不同宽度参数的RBF网络。

3 仿真应用

3.1 泛函逼近

考虑用RBF网络来逼近非线性函数[9]：

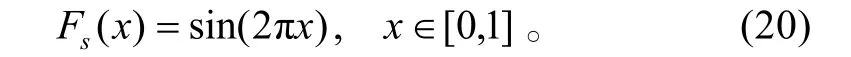
训练样本的产生方式如下：样本数L=100，训练样本输入x 服从区间[0,1]内的均匀分布，样本输出f(x)+e，其中，e为添加的高斯噪声，其服从均值为0、方差为0.22 正态分布。并且自变量x 以0.01为间隔在区间[0,1]上均匀取值，产生100个无噪声输出f(x)值作为测试数据集。

下面分别采用标准BP网络、SGA-RBF网络和IGA-RBF网络对上述非线性函数逼近。其中，图2为标准BP网络函数逼近曲线，图3为基于SGA 和IGA的RBF网络函数逼近曲线。从图2和图3的仿真结果比较可知，基于标准BP网络的函数逼近效果最差，而基于本文提出的IGA-RBF网络的函数曲线逼近效果最优。由此可以看出，基于本文IGA算法设计的RBF网络的泛化能力最强，体现了本文设计RBF网络方法的有效性。

3.2 故障模式的识别

反舰导弹自动驾驶仪是一个非常复杂的非线性系统，它包含有大量的模拟电路，因而很难有效地对其进行故障检测与诊断。下面以某型反舰导弹自动驾驶仪舵回路系统常见的8种故障（如电子放大器断开、齿轮卡死等）为例，对其进行动态测试。通过模型仿真预置故障，对采集的信号进行三层小波包（这里采用db4 小波）分解，根据基于小波包变换的特征提取算法[10]构造出该舵回路系统8种故障状态下的特征向量（8 维），建立“特征向量－系统状态”的对应关系。如表1所示为所构造出的具有表征系统8种故障状态能量的特征向量。

通过仿真实验可获取80组样本数据，并将其等分成两部分，分别用于网络训练和测试。将特征向量的维数8 作为网络的输入，而将这8种故障状态作为网络的输出，对基于IGA算法优化的RBF网络进行训练。然后，利用训练好的网络对待识别样本进行测试识别，其识别结果如表2所示，可见该网络能够较好地识别出导弹的故障模式。

为比较网络性能，分别采用标准 BP网络、SGA-RBF网络和本文IGA-RBF网络对故障模式进行训练和识别，识别的仿真结果比较见表3。从表3的比较结果看出，本文IGA-RBF网络明显比其他两种网络更能准确地对导弹故障模式进行识别，其识别正确率可达到97.5%，有效地实现了对导弹的故障检测与诊断。仿真结果表明，该IGA-RBF神经网络具有较强的模式分类和识别能力。

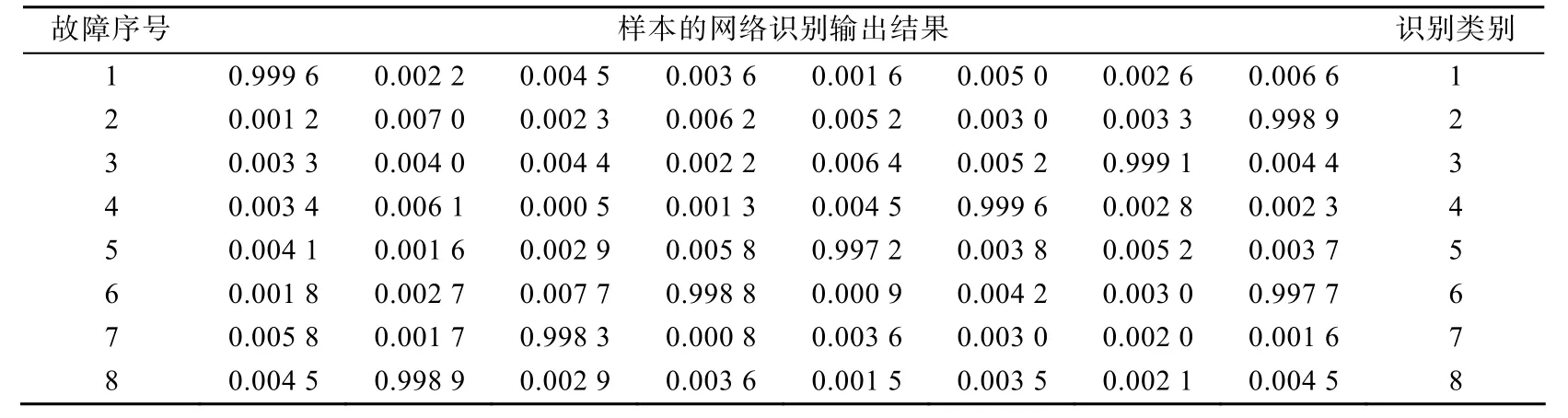
表2 本文IGA-RBF网络识别结果

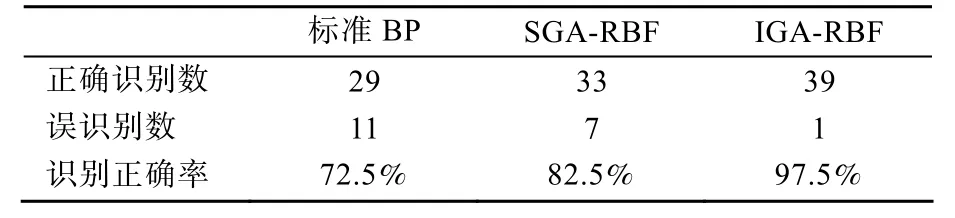
表3 三种网络的故障模式识别结果比较

4 结论

利用遗传算法优化RBF网络的隐节点数和基函数的中心值和宽度参数，可进一步提高网络预测精度，从而保证RBF网络的泛化能力，使RBF的学习上升到更高层次。针对传统BP网络及SGA算法的不足，本文提出了基于IGA的RBF神经网络，该网络引入自适应机制的实数编码的遗传算法，从初始群体生成及遗传算子操作等方面作了改进，并将其与梯度下降法混合交互运算，作为RBF网络的学习算法，应用于非线性函数的逼近和导弹故障模式的识别问题。仿真结果表明，基于IGA算法的RBF神经网络不仅结构简单，有较好的网络泛化性能，在工程上具有较高的理论意义和实际应用价值。

[1]HONGMEI LIU,PINGECHAO OUYANG,SHAOPING WANG.Fault detection based on RBF neural network in a hydraulic position servo system[C]//The 6th World Congress on Control and Automation.Dalian,China,2006:5708-5712.

[2]ZHIHONG QIE,XINMIAO WU,HITOSHI FURUTA,et al.The method of calculating hysteresis time of piezometric tube for earth-rock dam based on GA-RBF[C]//The 6th World Congress on Control and Automation.Dalian,China,2006:8523-8527.

[3]黄友锐.智能优化算法及其应用[M].北京:国防工业出版社,2008.

[4]尹靓,李连,刘东鑫.基于自适应遗传算法的航迹关联模型[J].海军航空工程学院学报,2009,24(3):272-276.

[5]田景文,高美娟.人工神经网络算法研究及应用[M].北京:北京理工大学出版社,2006.

[6]高玮.改进的快速遗传算法及其性能研究[J].系统工程与电子技术,2003,25(11):1427-1430.

[7]SRINIVAS M,PATNAIK L M.Adaptive probabilities of crossover and mutation in genetic algorithms[J].IEEE Trans.On SMC,1994,24(4):656-667.

[8]王小平,曹立明.遗传算法—理论、应用与软件实现[M].西安:西安交通大学出版社,2002:18-80.

[9]CHEN S,CHNG E S,ALKADHIMI K.Regularized orthogonal least squares algorithm for constructing radial basis function networks[J].International Journal of Control,1996,64(5):829-837.

[10]胡昌华,张军波,李学锋.一种基于小波和人工神经网络的故障检测与诊断方法[J].航天控制,2000,18(2):64-71.