基于最大度和随机游走的混合搜索算法

温巧林，司守奎，任东彦，谢宇鹏

（海军航空工程学院 a.研究生管理大队；b.基础部，山东 烟台 264001）

0 引言

随着人类生活日益网络化，各种网络信息急剧增长，网络搜索的重要作用也越来越明显。目前关于网络搜索仍有许多基本理论问题有待深入研究，例如何种网络才可以快速搜索？网络结构对网络搜索的效率有何影响？如何实现网络的快速搜索等等。

上世纪60年代，Stanley Milgram的小世界实验率先揭示了社会网络的小世界特性以及可搜索特性[1]。随后科学家们对网络搜索展开了一系列研究：先是Kleinberg在理论上对网络的搜索能力进行了研究[2-3]，然后Watts 等人又对此问题做了进一步的研究[4]，Adamic 等人则对Watts 等人的研究成果在Email网络上进行了验证[5-7]，而Clauset 等人提出了一个基于Kleinberg网格模型的动态网络模型[8]，他们也得出了和Kleinberg相似的结论。而关于网络搜索的算法研究，目前主要集中在提高搜索速度和控制算法本身对网络资源的占用这两个方面。当前，常见搜索算法在综合解决这两个方面问题时效果并不明显，本文将在分析常见搜索算法优劣的基础上提出一种综合改善这两方面因素的混合搜索算法。

1 几种常见搜索算法

通常用消息的传递过程来描述网络的搜索算法。搜索开始时，源节点按照一定的规则向它的一个或多个邻居传递查询消息。如果收到查询的邻居节点上不含有目标节点的信息，那么这些邻居节点再继续将查询传递给它们各自的邻居，重复这个过程直到目标节点被寻找到为止。常见的搜索算法很多，下面重点介绍广度优先搜索、随机游走搜索和最大度搜索算法。

1.1 广度优先搜索算法

广度优先搜索算法（breadth-first search，BFS）的基本思想是：从源节点s 开始，首先查询其所有的邻居节点，询问是否含有目标节点g，如果s的邻居中有节点含有了此目标节点，则将目标节点返回给源节点；如果没有邻居含有目标节点，则所有的邻居将查询继续传递给各自的邻居节点，一直到搜索到目标节点为止。BFS算法搜索速度很快，能够很快遍历网络，但其缺点也十分明显，随着网络规模的扩大，将会在网络中产生大量查询消息流量，造成网络流量急剧增加从而导致网络拥塞。

1.2 随机游走搜索算法

随机游走搜索算法（rand-walk search，RWS）是一个基础的动态过程，也是研究网络结构的一个很有用的工具。主要有无限制的随机游走搜索（URW）、不返回上一步节点的随机游走搜索（NRRW）和不重复访问节点的随机游走搜索（SARW）3种方式。三者的主要区别在于算法对访问节点的限制上。其中URW算法在搜索时不加任何限制地从其所有的邻居节点中随机选择一个作为下一个访问节点；NRRW在访问过程中除上一步访问节点之外，当前节点在其余的所有邻居中随机选择一个邻居节点；而SARW算法则将所有已访问节点排除在访问之外。

1.3 最大度搜索算法

最大度搜索算法（degree search，DS）最初是由Adamic 等人提出的[6-7]。由于对Gnutella网络的统计结果表明该网络的连接度服从幂律分布，Adamic 等人基于此提出了利用节点度的幂律分布特性进行搜索的构想。其基本思想是：源节点s 首先查询其度最大的邻居节点，询问是否含有目标节点g，如果此节点存储了目标节点，则它将目标节点返回给源节点；若没有，则它选择自己的度最大的邻居将查询传递过去，一直到搜索到目标节点为止。

2 基于最大度和随机游走的混合搜索算法

上面介绍了几种常见搜索算法的基本思想，可以看出，几种算法在搜索过程中存在着各自的优点和不足：广度优先算法搜索速度快，但会在网络中产生大量查询消息；随机游走虽然降低了查询消息，但搜索速度也随之下降了；最大度搜索虽能在两者之间取得一定的平衡，但是其搜索前进的“步伐”偏慢，且需要比较每个节点的度。因此，下面介绍我们设计的一种基于最大度和随机游走的混合搜索算法（degree and rand walk search，DRS）。它综合利用随机游走向前移动较快和最大度搜索信息利用率高的优点，在保持较快搜索速度的同时能有效控制查询消息量。

2.1 基本思想

DRS 搜索算法的基本思想是：在每个节点都认识自己的邻居并知道每个邻居的度的前提下，交替运用随机游走搜索和最大度搜索算法在网络中进行搜索。其基本过程如下，首先，源节点s 查询其度最大的邻居节点，询问是否含有目标节点g，如果找到目标节点，则它将目标节点返回给源节点；若没有，则它随机选择一个未访问过的邻居节点将查询传递过去，在下一步中如果节点依然没有搜索到目标节点，则再次运用最大度搜索进行查询。这样交替搜索直到搜索到目标节点为止。其基本搜索示意图过程如图1所示。

图1 利用DRS算法搜索源节点s与目标节点g之间的路径（搜索步数k=5）

2.2 算法设计

基于上面的分析，DRS 搜索算法设计如下。

1）构造集合E，用于存放已访问的节点，k=1。

2）判断源节点s是否为目标节点g。若是，则目标节点找到，停止搜索；否则，进入转步骤3）。

3）计算当前访问节点所有邻居节点尚未访问节点的度，选择其中度最大的节点作为下一步访问节点，k=k+1；如果这样的邻居节点不止一个，则在它们中随机选择一个节点作为访问节点；如果所有的节点都已经访问过，则返回到上一步所访问的节点。

4）判断此节点的邻居节点中是否有g。若有，则目标节点找到，搜索结束，否则转步骤5）。

5）对于第k+1步，在第k步访问节点的邻居节点中随机选择一个尚未访问的节点作为访问节点。

6）判断此节点的邻居节点中是否有g。若有，则目标节点找到，搜索结束，否则转步骤7）。

7）重复步骤3）～6），直至目标节点g 被找到。搜索结束。

3 搜索效率仿真

3.1 搜索效率

搜索算法主要是在提高搜索速度和控制查询信息量进行改进，因此本文在评价搜索效率时也将主要考察算法在这两方面的性能。算法的搜索速度由算法在搜索时需访问的步数决定。在一个节点数为N的网络中，当采用某种搜索算法时，则从这N个节点中随机选择出n个不同的源节点，然后对于每一个选择的源节点i，运用此搜索算法搜索源节点i到节点j的搜索步数tij(i≠j)。则源节点i到其他所有N−1个节点所需的搜索步数Ti为

因此，我们可定义网络的平均搜索步数T为

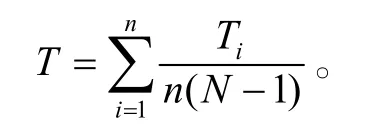
而算法的查询信息量则定义为搜索算法在搜索时查询邻居节点的次数。

3.2 仿真方法

仿真中构造出ER随机均匀网络、NW 小世界网络和BA 无标度网络3种网络模型。对于每种网络类型分别构造出N=20、30、50、75、100、150、200的7种网络规模，根据3.1节定义，选择的源节点个数为总节点个数的1/8，然后分别运用BFS、URW、NRRW、SARW、DS和DRS 求出各种算法的平均搜索步数。同时，为了比较各种算法在上述搜索过程中所产生的信息查询量大小，我们对仿真中的每个源节点，求出其访问网络中其他所有节点的信息查询量并取平均值，最后求出这些节点总的平均值从而得出搜索算法在这一网络类型中的平均信息查询量。

其中，对于ER随机均匀网络模型，设定其节点间连接概率为p=0.815；而NW 小世界网络模型的连接概率p=0.2，最近邻耦合系数k=2；对于BA无标度网络模型，其网络生成方式为初始节点m0=10，每次新添加m=5个节点。

3.3 仿真结果与分析

图2分别为几种搜索算法在3种网络类型中的平均搜索步数对比。从图中可以看出，最容易实现搜索的网络类型是小世界网络，其次为无标度网络，而在均匀网络中搜索速度较慢。另外，在均匀网络中网络的搜索步数是随着网络规模的增大而减少的，而在NW 小世界网络和BA 无标度网络中，搜索步数却随着规模的增大而增加的。而单纯就几种算法的搜索速度而言，BFS的搜索速度最快，DRS和DS次之，几种随机游走算法搜索速度最慢。

对于各种算法在搜索时对网络的信息查询量，从表1中统计数据可以看出，BFS 虽然平均搜索步数最少，但由于其每次都需询问所有的邻居节点，因此产生了非常大的查询消息量。在其他搜索算法中，查询消息从少到多依次是DRS算法、DS算法和3种随机搜索算法。虽然这几种搜索算法的平均信息查询量差距似乎不太明显，但是对于一个上百万甚至千万级的网络，网络中每个节点的一次查询就会在网络中产生大量的查询消息。因此，对于整个网络而言这样的改进是非常有意义的。

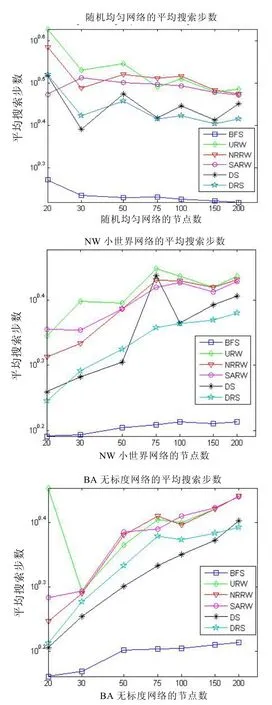
图2 各种搜索算法在均匀网络、NW 小世界网络和BA 无标度网络中的平均搜索步数

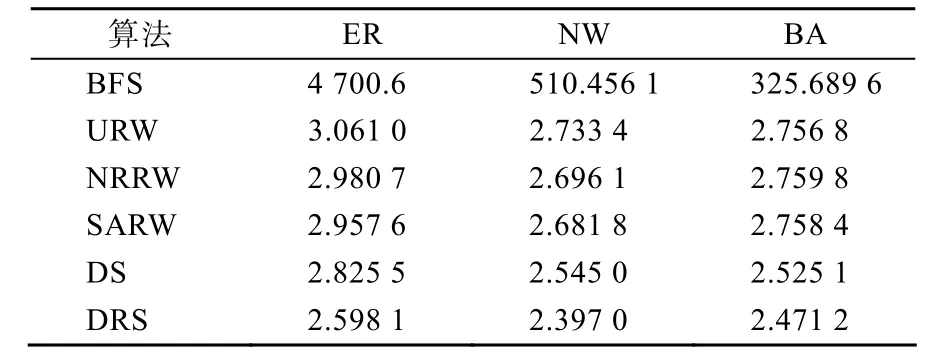
表16 种搜索算法在不同网络类型中的平均信息查询量

从上述仿真可以看出，DRS 搜索算法无论是在提高搜索速度方面还是在控制搜索过程中的信息查询量都比较好，因此是一种较为理想的搜索算法。

4 结论

随着网络理论研究的不断兴起，网络搜索问题正逐渐引起研究人员的注意。在网络搜索算法研究中，如何在提高网络搜索速度的同时控制好搜索过程中所产生的查询消息，是需要深入研究的问题。本文所提出的基于最大度和随机游走的搜索算法综合利用最大度搜索利用邻居节点信息充分和随机游走快速访问远程连接的优势，在提高了网络搜索速度的同时也较好地控制了信息查询量，搜索效果比较理想。

[1]MILGRAM S.The small world problem[J].Psychology Today,1967,2∶60-67.

[2]KLEINBERG J.Navigation in a small world[J].Nature,2000,406∶845.

[3]KLEINBERG J.The small-world phenomenon∶an algorithmic perspective[C]//Proceedings of the 32nd Annual ACM Symposium on Theory of Computing.New York,2000∶163-170.

[4]WATTS D J,DODDS P S,NEWMAN M E J.Identity and search in social networks[J].Science,2002,296∶1302-1305.

[5]ADAMIC L A,ADAR E.How to search a social network[J].Social Networks,2005,27(3)∶187-203.

[6]ADAMIC L A,LUKOSE R M,PUNIYANI A R,et al.Search in power-law networks[J].Phys.Rev.E.,2001,64∶046135.

[7]ADAMIC L A,LUKOSE R M,HUBERMAN B A.Local Search in Unstructured Networks[M].In S.Bornholdt and H.G.Schuster (eds.),Handbook of Graphs and Networks,Berliln∶Wiley-VCH,2003.

[8]CLAUSET A,MOORE C.Cond-mat/0309415.How do networks become navigable[K].