基于不敏变换的GDOP计算

谭顺成，曾庆和，王国宏，王 娜，2

（1.海军航空工程学院 信息融合技术研究所，山东 烟台 264001；2.92941部队，辽宁 葫芦岛 125001）

0 引言

系统对目标的定位误差与目标相对于定位站的几何关系密切相关。为了评估系统的定位性能，引入定位精度几何稀释（Geometrical Dilution of Precision，GDOP）作为评价指标[1-3]。通过对GDOP的计算，可以评价定位系统中各定位站的测量精度以及定位站的几何布局对系统定位能力的影响。

对于非线性系统，其GDOP的计算通常是一个强非线性的问题，而现有的文献一般采用线性化的方法对其进行求解[3-6]。在系统定位精度较高且定位函数的非线性较弱的情况下，通过线性化方法得到的GDOP与实际定位误差基本相符合。但是在某些情况下，当定位精度较低或定位函数的非线性较强时，线性化方法得到的GDOP 并不可靠，对系统定位能力的分析造成严重的影响。

不敏变换（Unscented Transformation，UT）是用于计算经过非线性变换的随机变量的一种新方法，可以非常方便地应用于非线性系统的状态估计，因而在许多方面得到广泛应用[7-11]。UT的基本思想是：近似非线性函数的概率密度分布比近似其函数本身更容易。因此，UT通过选取一系列完全体现高斯密度真实均值和协方差的σ 采样点对非线性函数的PDF 进行近似，而不是对非线性系统进行线性化处理。本文针对强非线性系统，提出一种基于UT的GDOP计算方法，并将其与线性化求解GDOP的方法进行了分析和比较。

1 基于UT的GDOP计算

以三维非线性定位系统为例，GDOP的定义式

假定z为nz维随机量测向量，其均值和协方差分别为和Pz，y为三维随机定位向量，其均值和协方差分别为为非线性定位函数

与文献[7]中的方法类似，基于UT方法的GDOP计算过程如下所述：

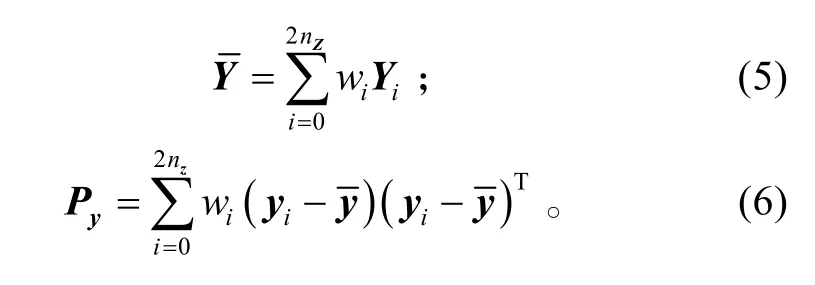
令

将式(7)代入式(1)得

2 仿真分析

本节以文献[1]给出的时差无源定位模型为例，分别对基于线性化方法和UT方法的GDOP 进行计算，并与平均系统定位误差进行分析和比较。

2.1 仿真场景

图1为三站时差无源定位的示意图。3个无源传感器1、2和3分别位于点A、O和B。

图1 三站时差无源定位原理

由文献[1]可知，该系统的定位方程为

其中，

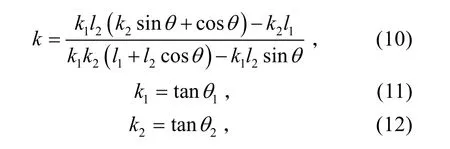
式中：点(x,y)表示辐射源位置；l1=l2=40 km分别表示传感器1、2和传感器2、3之间的量测距离；θ为传感器1、2和传感器2、3的基线之间的夹角；1θ和2θ分别为辐射源主波束依次扫过传感器1、2和2、3形成的夹角。

设辐射源扫描周期为T=10 s，主波束依次扫过传感器1、2和2、3的扫描时差分别为Δt12和Δt23，则

假设量测距离1l、l2和扫描时差Δt12、Δt23的量测误差是相互独立的零均值高斯随机噪声，其标准差分别为为了计算简便，令θ=0 °（即 3个传感器位于同一直线上），基于线性化方法和UT方法的GDOP计算分别如式(15)和式(16)所示。

式中：

其中，

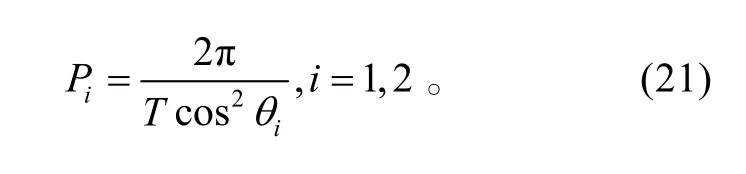
而 PUT,y由第1节的计算方法得到。

2.2 仿真结果

图2、3分别为线性化方法和UT方法得到的GDOP分布，图4为基于200次Monte Carlo仿真取平均得到的系统定位误差分布。基于对称性，文中只给出了各分布图的上半部。

图2 基于线性化方法的GDOP分布

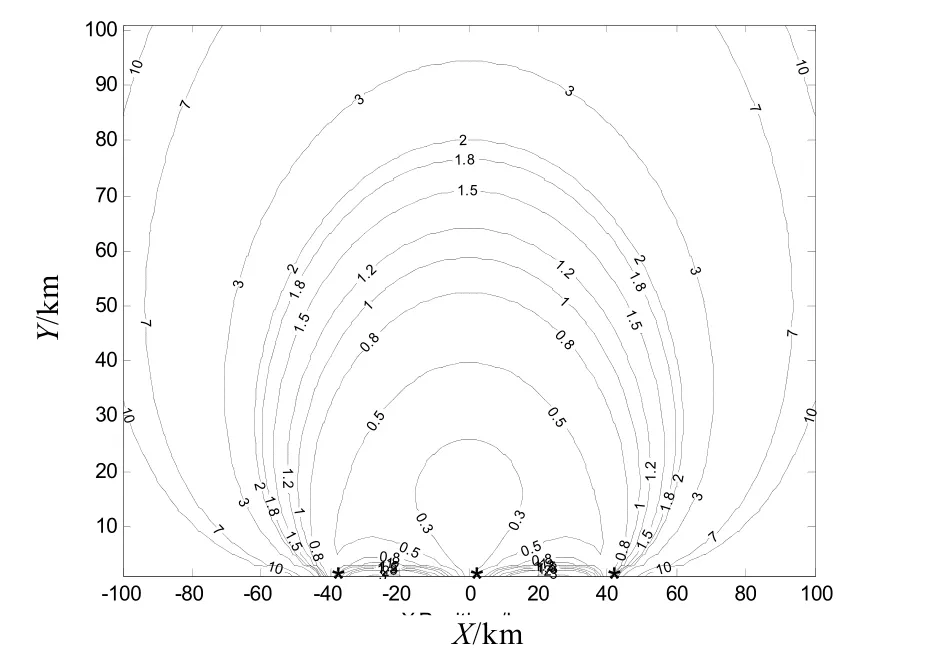
图3 基于UT方法的GDOP分布

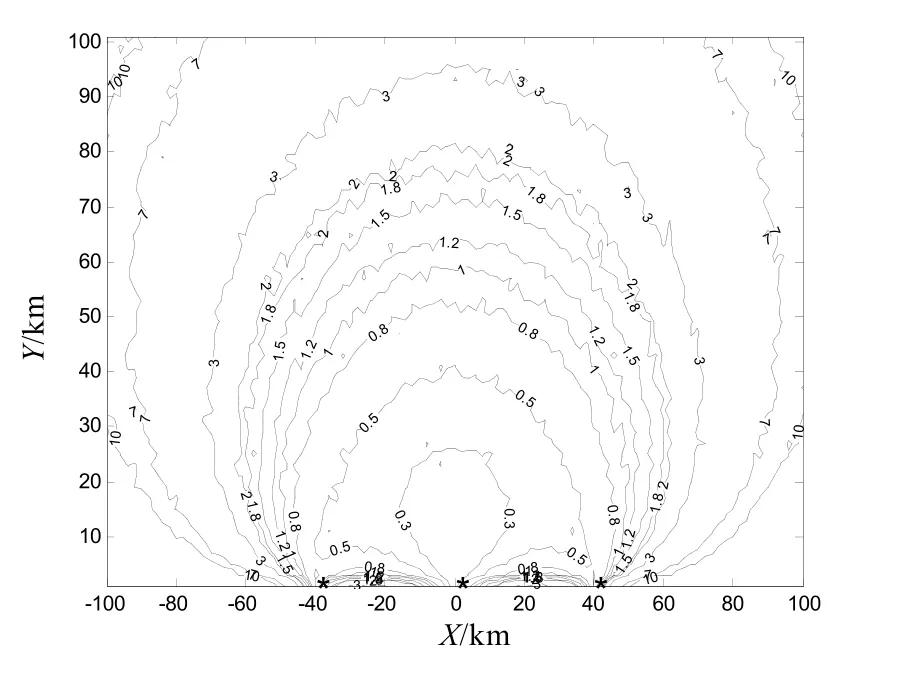
图4 基于200次Monte Carlo仿真取平均的系统定位误差分布

为了方便比较，表1给出了某些点分别基于两种方法得到的GDOP以及这些点的平均系统定位误差。

从图2和图4可以看出，当目标距传感器较远时，基于线性化方法的GDOP分布与平均系统定位误差相近；而当目标距传感器较近时，其GDOP分布严重偏离平均系统定位误差。而由图3和图4可以看出，基于UT方法得到的GDOP分布与平均系统定位误差分布非常接近。

从表1可以得出相同的结论。由仿真结果可知，当定位系统的非线性较强时，基于线性化方法得到的GDOP 并不可靠，而基于UT方法得到的GDOP则能够较准确的反映系统定位误差。造成这种结果的可能原因是：基于UT方法的GDOP可以精确到二阶项，而线性化方法仅保留了泰勒展开式的第一阶项，因此造成较大的误差。

表1 某些点的GDOP和平均定位误差 km

3 结论

本文首先提出了一种基于UT方法的GDOP计算方法，然后通过一个三站时差无源定位的例子证明：在定位系统的非线性较强的情况下，基于线性化方法得到的GDOP 并不可靠，而基于UT方法得到的GDOP 则能比较准确的反映系统定位误差。因此，强非线性情况下利用线性化方法计算GDOP 必须特别慎重，而基于UT的方法不失为一种较好的可选择方法。

[1]徐汉林.时差无源三站精确定位技术研究[J].电子对抗技术,1998,13(1)∶15-23.

[2]I SHARP,K YU,Y J GUO.GDOP Analysis for positioning system design[J].IEEE Trans.on Vehicular Technology,2009,58(7)∶3371-3382.

[3]WANG Z,ZHANG J.Analysis and simulations of GDOP in the location of GPS[C]//Proc.SPIE,2007,6795(3)∶721-726.

[4]BECKER K.Passive localization of frequency-agile radars from angle and frequency measurements[J].IEEE Trans.on Aerospace and Electronic Systems,1999,35(4)∶1129-1143.

[5]XIU J J,HE Y,WANG G H,et al.Constellation of multisensors in bearing-only location system[J].IEEE Proc-Radar Sonar Navig.,2005,152(3)∶215-218.

[6]BECK A,STOCIA P,LI J.Exact and approximate solutions of source localization problems[J].IEEE Trans.Signal Processing,2008,56(5)∶1770-1778.

[7]JULIER S J,UHLMANN J K,DURRANT-WHYTE H F.A new approach for filtering nonlinear systems[C]//Proceedings of American Control Conference.Seattle,WA,1995∶1628-1632.

[8]WAN E A,MERWE R VAN DER,NELSON A T.Dual estimation and the unscented transformation[J].Advances in Neural Information Processing Systems,2000∶666-672.

[9]JULIER S J,UHLMANN J K,DURRANT-WHYTE H F.A new method for the nonlinear transformation of means and covariances in filters and estimators[J].IEEE Trans.Automatic Control,2000,45(3)∶477-482.

[10]LEFEBVRE T,BRUYNINCKX H,SCHUTTER J DE.Comment on a new method for the nonlinear transformation of means and covariances in filters and estimators[J].IEEE Trans.on Automatic Control,2002,47(8)∶1406-1409.

[11]ST-PIERRE M,GINGRAS D.Comparison between the unscented Kalman filter and the extended Kalman filter for the position estimation module of an integrated navigation information system[C]//IEEE Intelligent Vehicles Symposium University of Parma,Parma,Italy 1447,2004∶831-835.