基于变步长LMS算法的线性调频引信噪声抑制

路翠华，李国林，熊 波

（海军航空工程学院 a.七系；b.兵器科学与技术系，山东 烟台 264001）

0 引言

调频引信根据回波信号与发射信号的频差来提取目标信息，但是压制性干扰的存在可以阻碍引信对目标信息的正常检测。压制性干扰的最佳干扰波形就是随机性最强的波形，在平均功率限定的条件下，正态分布噪声的随机性最大，为最佳压制性干扰波形。自适应滤波技术发展至今，已成为干扰抑制[1-6]、回波消除[7]、泄露抵消[8]等方面重要的技术手段。本文将自适应滤波技术应用到线性调频引信中，用来对压制性高斯白噪声进行抑制。

自适应滤波算法的选择影响滤波器的收敛速度和精度。LMS算法是一种用瞬时值估计梯度矢量的自适应算法，具有算法简单、计算量少的优点，因而得到了广泛的应用，但其存在收敛速度、跟踪速度和收敛精度的矛盾。为了解决这一矛盾，人们提出了变步长自适应滤波算法。文献[9]提出其步长因子可随迭代次数n的增加而逐渐减少的自适应滤波算法；文献[10]提出一种时间平均估值梯度的自适应滤波算法；文献[11]提出一种步长因子µ 正比于误差信号e (n)大小的自适应滤波算法；文献[12]提出一种步长因子µ 与e(n)和 x (n)的互相关函数的估值成正比的自适应滤波算法；文献[13]给出了Sigmoid函数变步长LMS算法；文献[14]也提出了一种变步长自适应滤波算法。本文采用文献[14]提出的变步长自适应滤波算法，该算法满足变步长自适应滤波算法的步长调整原则[15]，并克服了Sigmoid 函数变步长LMS算法在自适应稳态阶段仍有较大步长变化的不足。

1 线性调频引信的工作原理

线性调频引信为锯齿波调制，发射波的频率按锯齿波规律变化。其发射、反射和差频信号变化规律如图1所示。

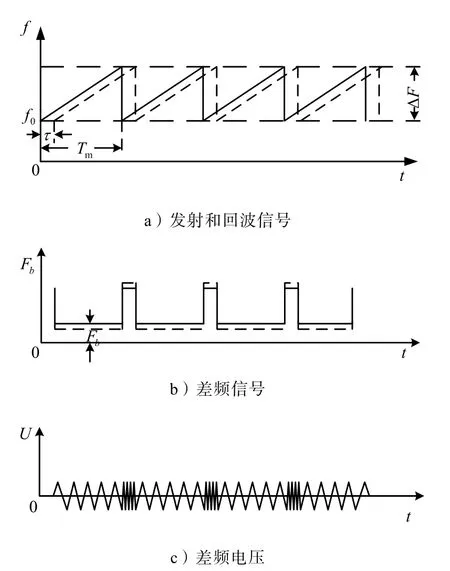
图1 锯齿波调制时间—频率曲线

图1a）为发射与回波信号的时间—频率曲线。实线为发射信号频率 ft，虚线为回波信号频率 fr，f0为载波频率，∆F为最大频偏，Tm为调制信号周期。图1b）为混频器输出端差频信号的时间—频率曲线，其中，Fb表示差频频率，为nT ～nT +τ 期间的差频。图1b）中虚线为考虑多普勒效应影响时的情况。图1c）为混频器输出端差频信号电压Ui与时间的曲线。由图1可求得发射信号频率 ft与回波信号频率 fr的表达式为：

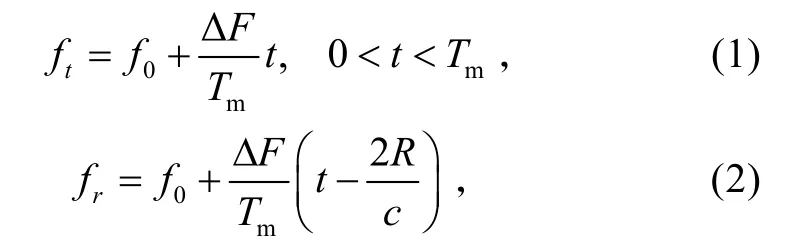
式中：c为电磁波的传播速度。

差频bF为：

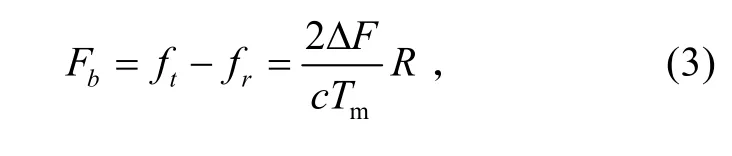
即

由式(3)、(4)看出，当调制参数mT 和 ∆F 一定时，差频bF 与距离R 成正比。

若存在压制性干扰，干扰信号为正态分布的噪声。通过线性调频引信通带的压制性噪声太强时，引信将无法正确测得差频信号频率bF，从而无法正确得到导弹与目标的距离R，此时需要对引信通带内的噪声进行抑制。

2 噪声抑制原理

线性调频信号中含有高斯白噪声时，调频信号是可预测的，但高斯白噪声的可预测性比较差，利用两者可预测性的差异进行噪声抑制。噪声抑制原理如图2所示。

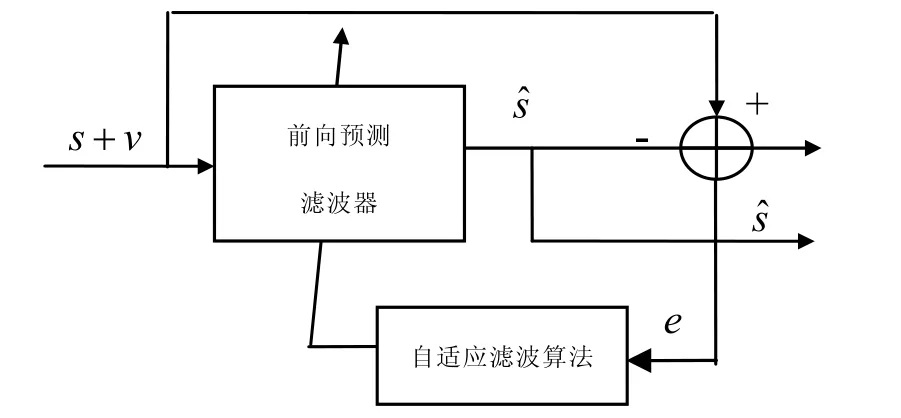
图2 噪声抑制原理

设含有噪声的信号为x，x=s+v，其中s为线性调频信号，v为高斯白噪声。利用前向预测滤波器可得到信号s的前向预测信号。误差e=s +v−，根据误差e 调整前向预测滤波器的权值，使→s，从而使e → v，达到噪声抑制的目的。

因为引信工作时间比较短，所以要选计算量少、收敛速度快的自适应滤波算法。本文采用文献[14]提出的变步长自适应滤波算法。该算法初始收敛阶段较大，对应的µ (n)较大，算法收敛速度较快；当算法进入稳态时，达到最小，此时 µ (n)也达到最小，由此得到最佳Wiener 解。算法如下：

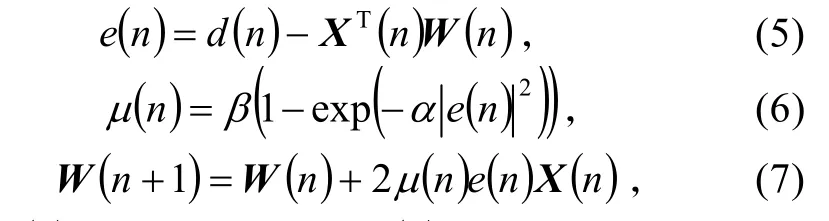
式中：d (n)为期望响应；X (n)为输入信号矢量；W (n)为权值；µ (n)为步长因子；参数α＞0控制函数的形状；参数β＞0控制函数的取值范围。

3 噪声抑制性能仿真与分析

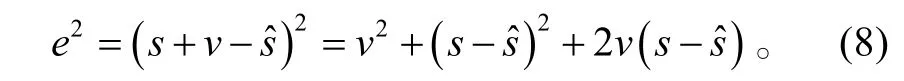
对式(8)两边取数学期望，则

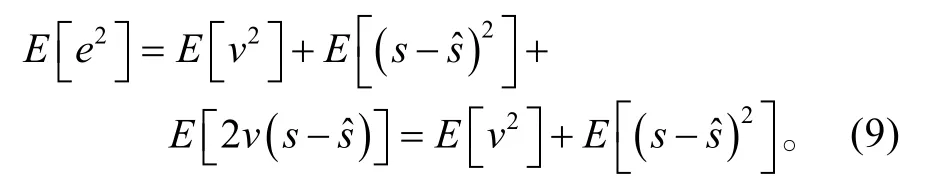
为深入贯彻中央全面从严治党要求和乡村振兴战略，培养优秀基层党建和社会管理人才，提高基层经济发展管理质量，11月10日-16日，十二师二二二团首批28名由连队、社区“两委”和致富带头人、合作社社长组成的考察团赴对口援疆省市，山西长治市开展了为期一周的观摩学习。

实际上很难达到自适应滤波的理想情况，下面通过仿真来分析线性调频引信采用变步长LMS算法进行噪声抑制的性能。取变步长LMS算法中的参数α、β为：α=1 000，β=0.001 54（滤波参数α、β 选取依据经验值）。当SNB=0 dB时，线性调频引信采用变步长LMS算法进行噪声抑制的效果如图3所示。

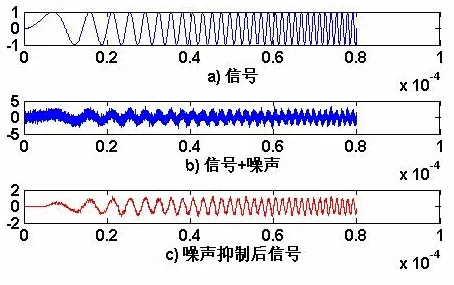
图3 SNB=0 dB时噪声抑制效果

当SNB=−5 dB时，线性调频引信采用变步长LMS算法进行噪声抑制的效果如图4所示。

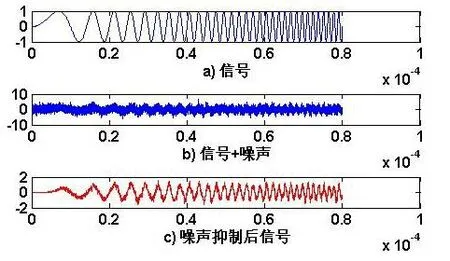
图4 SNB=−5 dB时噪声抑制效果

图3a）和图4a）为原始信号，图3b）和图4b）为含有噪声的信号，图3c）和图4c）为噪声抑制后的输出信号。由图3c）可以看出，SNB=0 dB时，线性调频引信采用变步长LFM算法很好地抑制了线性调频信号中的噪声。由图4c）可以看出，SNB=−5 dB时，噪声抑制后的信号虽然仍旧含有部分噪声，但信噪比得到了明显的改善。

当SNB=−10 dB时，线性调频引信采用变步长LMS算法进行噪声抑制的效果如图5所示。

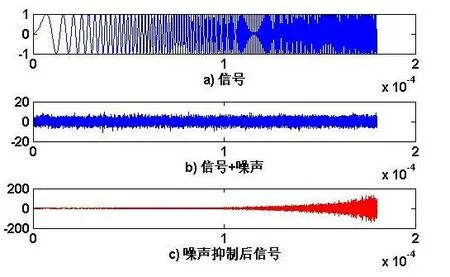
图5 SNB=−10 dB时噪声抑制效果

由图5c）可以看出，当SNR=−10 dB时，变步长LMS算法的参数为α=1 000，β=0.001 54时，算法不收敛，达不到很好的噪声抑制效果。此时，需要调整变步长LFM算法的参数α、β。

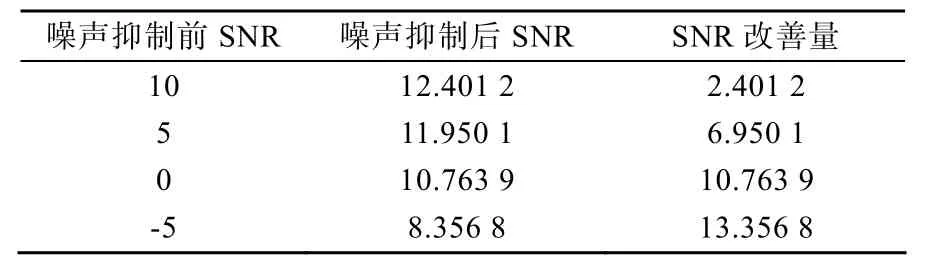
表1 噪声抑制前后信噪比及改善量

由表1可以看出，线性调频引信利用变步长LMS算法进行噪声抑制明显改善了信噪比，并且在算法收敛的条件下，信噪比越小，信噪比的改善量越大。

4 结论

将自适应滤波技术应用到线性调频引信中，用来对压制性噪声进行抑制。根据线性调频信号和噪声可预测性的差异，利用前向预测滤波器对噪声进行抑制，分析了噪声抑制原理，自适应滤波算法采用文献[14]提出的变步长LMS 自适应滤波算法。取变步长LMS算法中参数 α=1 000，β=0.001 54，通过仿真分析可以发现，在SNB=−5dB时仍然可以达到很好的噪声抑制效果，在算法收敛的条件下，信噪比越小，信噪比的改善量越大。

[1]谢春健.基于自适应滤波的扩频通信系统抗干扰研究[D].西安:西北工业大学,2005.

[2]胡军锋.宽带通信中的窄带干扰抑制技术研究[D].西安:西安电子科技大学,2004.

[3]周红彬.直接序列扩频通信中窄带干扰的识别和抵消[D].西安:西安电子科技大学,2003.

[4]李红霞.直接序列扩频信号中多窄带干扰的自适应抑制技术[D].成都:电子科技大学,2001.

[5]SAMI AROMAA,PERTTI HENTTU,MARKKU JUNTTI.Transform-selective interference suppression algorithm for spread-spectrum communications[J].IEEE SIGNAL PROCESSING LETTERS,2005,12(1):49-51.

[6]HAOSHEN,ANTONIA PAPANDREOU-SUPPAPPOLA.Wideband time-varying interference suppression using matched signal transforms[J].IEEE Trans.Signal Process.,2005,53(7):2607-2612.

[7]林耀荣.自适应滤波理论及其在回波消除中的应用研究[D].广州:华南理工大学,1999.

[8]韩俊杰,党怀锁,焦光龙.FTLMS算法在引信泄漏信号对消器设计中的应用[J].弹箭与制导学报,2002,22(4):66-68.

[9]GITLIN R D,WEINSTEIN S D.On the design of gradient algorithms for digitally implemented adaptie filters[J].IEEE Trans.on CT,1973,20(2):125-136.

[10]GITLIN R D,WEINSTEIN S D.The effects of large interference on the tracking capability of digitally implemented echo cancellers[J].IEEE Trans.on COM,1978,26(6):833-839.

[11]YASUKAWA H,SHIMADA S,FURUKRAWA I.Acoustic echo canceller with high speech quality[C]//ICASSP,1987:2125-2128.

[12]叶华,吴伯修.变步长自适应滤波算法的研究[J].电子学报,1990,18(4):63-69.

[13]吴光弼,祝琳瑜.一种变步长LMS 自适应滤波算法[J].电子学报,1994,22(1):55-60.

[14]高鹰,谢胜利.一种变步长LMS 自适应滤波算法及分析[J].电子学报,2001,29(8):1094-1097.

[15]谭景繁,欧阳景正.一种新的变步长自适应滤波算法[J].数据采集与处理,1997,12(3):171-174.