波流混合作用的完全非线性数值水槽模型

宁德志,陈丽芬,田宏光

(1.大连理工大学海岸和近海工程国家重点实验室,辽宁大连 116024;2.南京水利科学研究院水资源与水利工程科学国家重点实验室,江苏南京 210029)

随着计算机技术和现代数值方法的发展,完全非线性数值水槽技术作为一种非常有效的工具已经解决了许多复杂的水波问题[1-5].从以往的研究成果可以发现,完全非线性数值数槽模型大多被应用于纯波浪问题.然而,在实际的工程问题中,波浪和水流往往同时存在,由于水流的存在,物面上波动势的边界条件发生变化,波浪对结构物的绕射也相应发生变化,从而波浪对结构物的荷载以及在结构物上的爬高也受到水流的影响.这样再用纯波浪理论和模型来计算就会导致很大的误差,无法指导工程设计和作业.在许多海洋工程项目中,准确预测结构物在波浪和水流共存环境下的荷载和运动响应是非常重要的.国内外很多专家学者在此方面也开展了大量的工作,目前比较成熟的研究大多还是基于线性和摄动展开理论,如采用频域方法研究波流混合与结构物的作用问题[6-8],采用时域方法研究波流混合与结构物作用的线性问题[9].

高阶边界元法作为目前国际上先进的算法之一,已经在很多领域得到广泛应用,特别是在非线性水波问题的时域模拟方面.然而在完全非线性波流混合作用方面的应用还不多见.本文将采用时域高阶边界元方法建立波流混合作用的完全非线性数值水槽模型,研究波流混合作用与纯波浪相比的波面变化及非线性变化情况.

1 数学模型

1.1 控制方程和边界条件

在假定流体无粘和流动无旋的前提下考虑波流混合传播问题,整个流域可用速度势来描述.建立一个笛卡尔坐标系Oxyz如图1所示,使得z=0位于静水面上,且z轴向上为正,波浪传播方向与 x轴正向保持一致.这里,自由水面、固体边界分别用Sf、SN(包括水底Sd、水槽两个侧面Sc和入射边界面 S1)表示.考虑到水流的作用,流域内的整体速度势可以表示为Φ=φ(x,y,z,t)+U0x,其中U0代表水流速度,φ(x,y,z,t)表示由波浪引起的速度势,速度势Φ和φ都满足Laplace方程和下列边界条件.

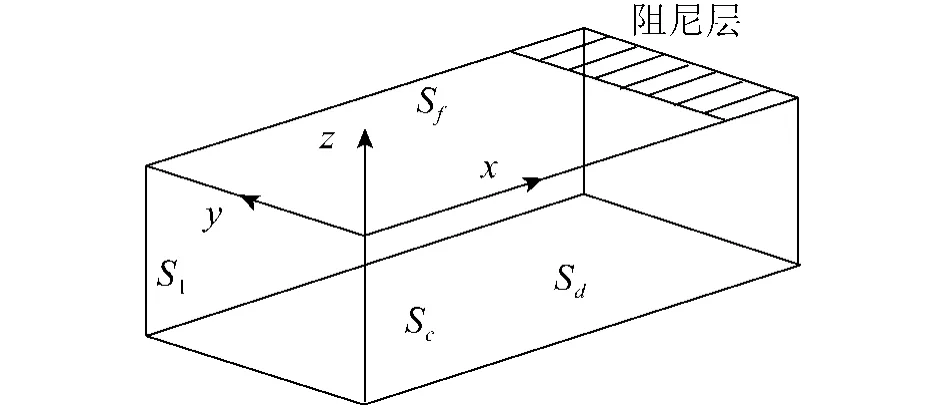
图1 波流水槽示意图Fig.1 Definition sketch of the wave-current tank

在瞬时自由水面Sf上,满足完全非线性运动学和动力学边界条件.本文采用混合欧拉-拉格朗日法更新自由水面,故自由水面边界条件可以写成以下形式[10]:

式中:XF(t)=(xF(t),yF(t),zF(t))为瞬时自由表面上任意流体质点的位置矢量,zF=η(x,y,t)代表自由水面高程,g是重力加速度,物质导数流体质点速度v=▽Φ,也就是说波面随着流体质点的速度进行更新.

在水底和水槽侧壁上满足固壁不可渗透边界条件

在水槽入射边界上给定波浪传播速度的二阶斯托克斯理论解[11]:

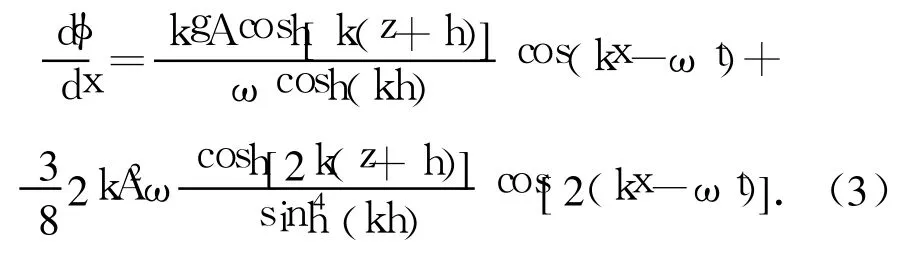
式中:k是波数,ω是波浪角频率,h是水深,A是入射波幅.由于水流的存在,波数k和角频率ω将满足如下色散方程关系:

与其对应的波流混合传播的线性波面理论表达式为

从式中可以看出,当水流速度为0时,式(4)和(5)与纯波浪的表达式一致.

由于本问题是在时域内求解,还要给定初始边界条件,下列静水面边界条件被满足:

在水槽的末端,采用在下游水面区加一人工阻尼层来吸收向右传播的波浪,防止波浪发生反射,通过在自由面运动学和动力学边界条件式(1)中加入阻尼项来实现[12],即

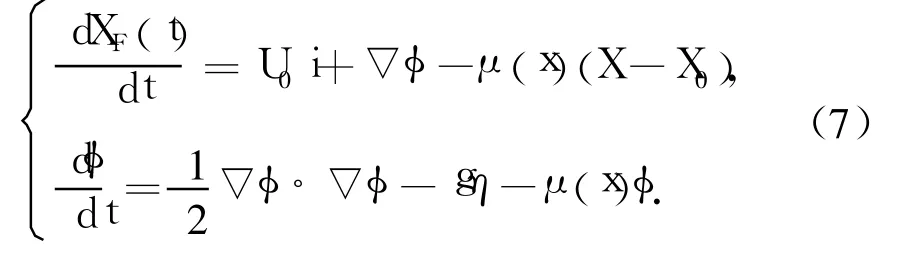
其中,

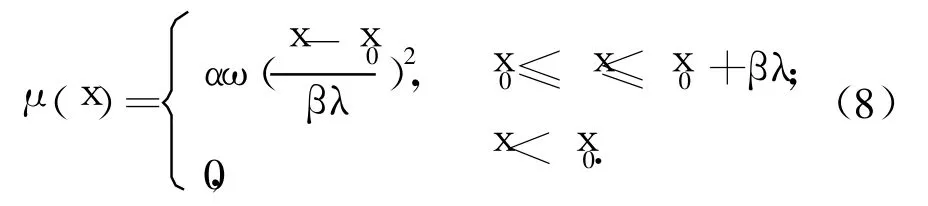
式中:X0=(x0,y0,0)是指水质点静止时的位置,x0为阻尼层起始坐标,α为阻尼系数,βλ为阻尼层长度,λ为波长,β为岸滩宽度系数,本文取α=1,β=1.

1.2 数值求解

在整个流域内应用格林第二定理,则上述边值问题可转化为如下的边界积分方程:

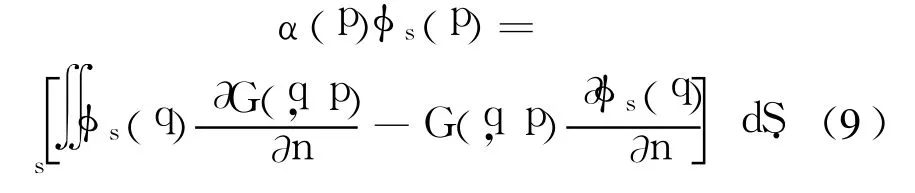
式中:p=(x,y,z)为源点,q=(x0,y0,z0)为场点, α(p)为固角系数.边界S包括自由水面Sf和固体表面 SN,G是简单格林函数,考虑到计算域的对称性,可以写出如下形式:

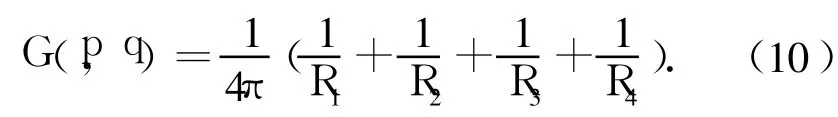
其中,

这样积分区域仅仅在一半的计算域上进行,且不包括水底.

本文用高阶边界元离散计算域成一些曲面单元,对每个单元通过数学变换,将其转换成参数坐标(ξ,ζ)下的等参单元,采用二次形状函数插值方法保证单元内物理量分布的连续性.单元内任一点的几何坐标和速度势等物理量都可以由各节点上的值和形状函数表示成如下形式[13]:

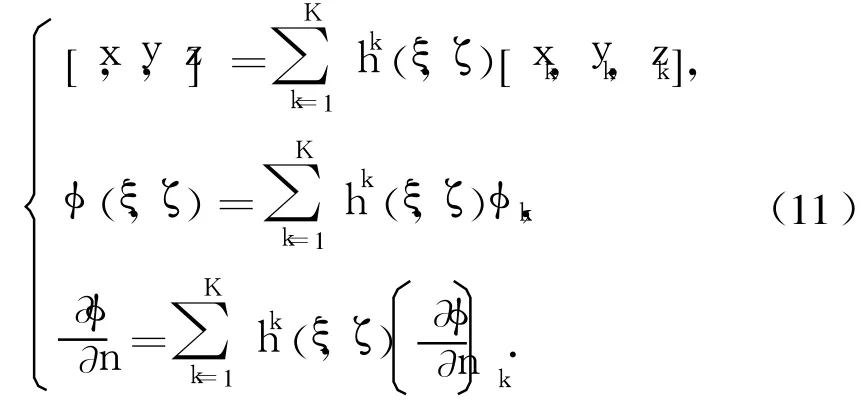
通过配点法,将源点p分别取在各个节点上,可建立如下线性方程组:

由于积分边界是不断地随着时间变化的,在每一计算时刻都要重新建立系数矩阵 A和B,并且在每一计算时刻都要对方程进行求解.

计算中认为当前时刻物面 SN上的速度势法向导数和自由水面Sf上的速度势是已知的,根据积分方程(9)计算当前时刻物面SN上的速度势和自由水面Sf上的法向速度,然后应用四阶Runge-Kutta法,根据自由水面条件式(7)计算下一时刻的水质点位置和自由水面Sf上的速度势,再对自由水面重新划分网格,重新应用积分方程计算下一时刻物面上的速度势和自由水面上的法向速度.这样计算周而复始,直到计算结束.

1.3 网格重新划分

由于自由水面的变化,计算域的大小每一时间步都在改变,网格相应地跟着改变,为了防止由于水质点运动导致网格大小不均匀引起数值不稳定问题,需要定期进行网格重新划分来调整这种网格不均匀问题.网格重新划分在直立面(如水槽入射面和侧壁)非常容易,对于自由水面上的网格重新划分,首先通过下式确定新节点计属于重新划分前哪一个单元:

式中:S0是未重新划分单元的面积,Si是新节点与未重新划分单元中 2个相邻节点所组成的三角形的面积,M是环绕新节点所形成的三角形单元总数,当参数 ε趋于 0时,认为该节点隶属于这个单元.然后求出新节点在所在旧单元中的形状函数,最后通过式(11)得到新节点处的空间位置和速度势,详细过程可参见文献[14].

2 数值计算及讨论

作为算例,考虑静水深h=1.0m水槽中完全非线性波流混合传播情况,研究波流同向、反向和纯波浪3种工况.取波浪角频率w=1.506 76,入射波幅A=0.05m,水流速度U0=0.313m/s.经过开展数值收敛性试验选定时间步长Δt=T/80(T为波浪周期),空间步长Δx=Δy=λ/20(λ为波长),水槽尺度定义为 5λ×0.1λ,垂向布置 4个单元,水槽末端布置长度为1.5λ的人工阻尼层.

从图2中可以看出,波(流)传到8T时已达到稳定,3种工况下 8T和 10T的波面已经完全重合,说明本模型已达到数值收敛,对波浪和波流混合问题都可以得到收敛的数值结果.

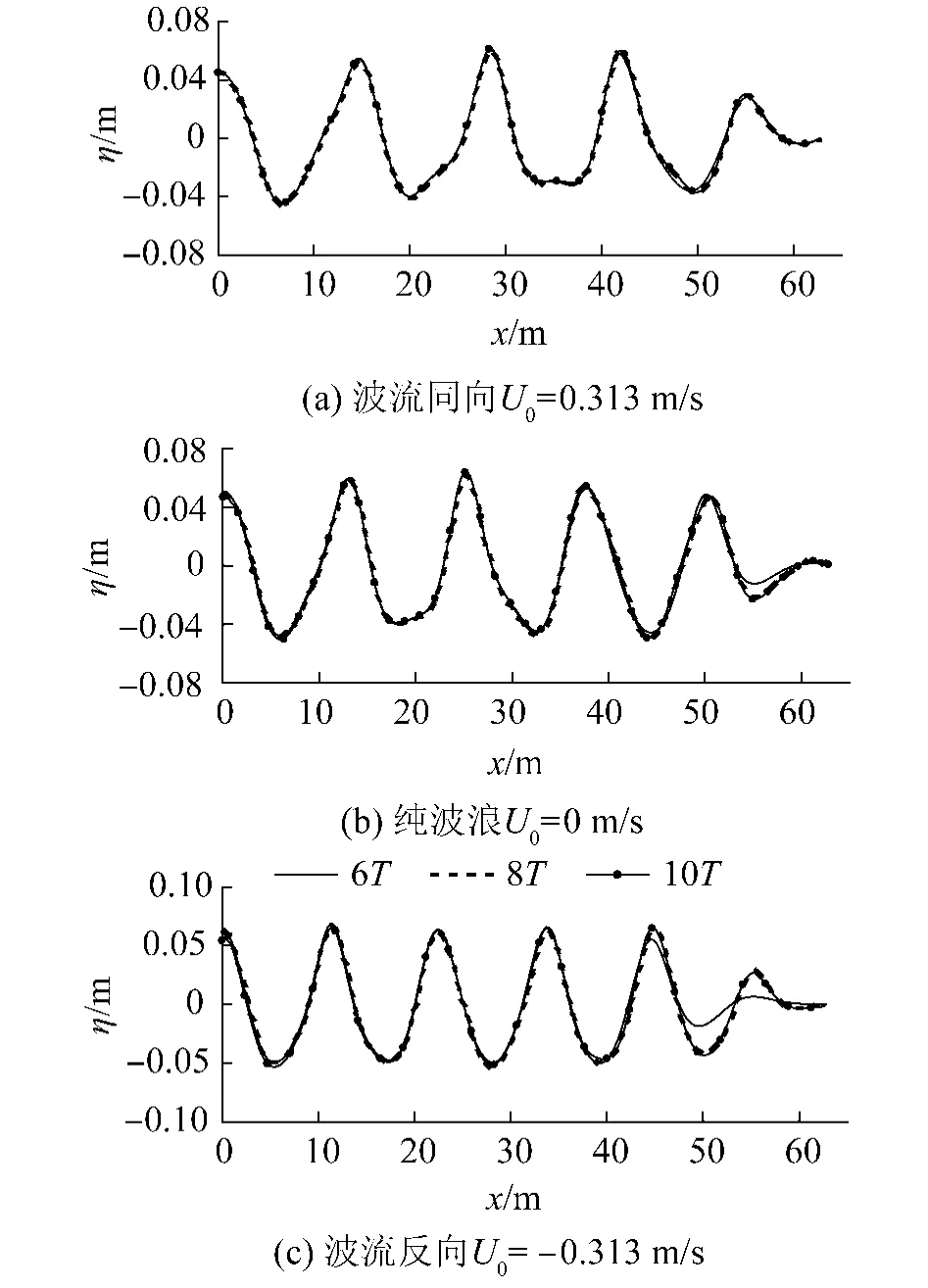
图2 t=6T、8T和10T时水槽中线波面分布图Fig.2 Distribution of wave elevation along the symmetry of wave flume at t=6T,8T and 10T

图3～5是分别距离水槽入射边界 5.0 m和10.0m两点处波流同向、纯波浪和波流反向 3种工况下的波面时间历程及本文数值结果与已发表Boussinesq模型结果[10,15]的对比.从图中可以看出,各点在各工况下的波面都保持稳定传播,且本文数值结果与Boussinesq模型结果吻合的很好,进而证明本模型的准确性.

下面研究水流对波浪非线性的影响.图 6是x=5.0 m和 10.0 m处,水流同向、无水流和波流反向时的波面时间历程图.从图中可以看出,各工况下两点处都经历一定的缓冲时间达到稳定状态,波面幅值保持不变,但是由于本算例属于浅水问题,各点之间存在一定的能量交换,以至于各点之间的波幅不同;波流同向与纯波浪相比波浪的传播有超前性,而波流反向与纯波浪相比有滞后性,也就是说波浪同向时的传播速度最小,即波数最大,这与色散关系式(5)得到的结论是一致的;3种工况下波流同向时波峰最小,波流反向时波峰最大,进而说明波流反向时使得波浪非线性增强,波流同向时非线性减弱.

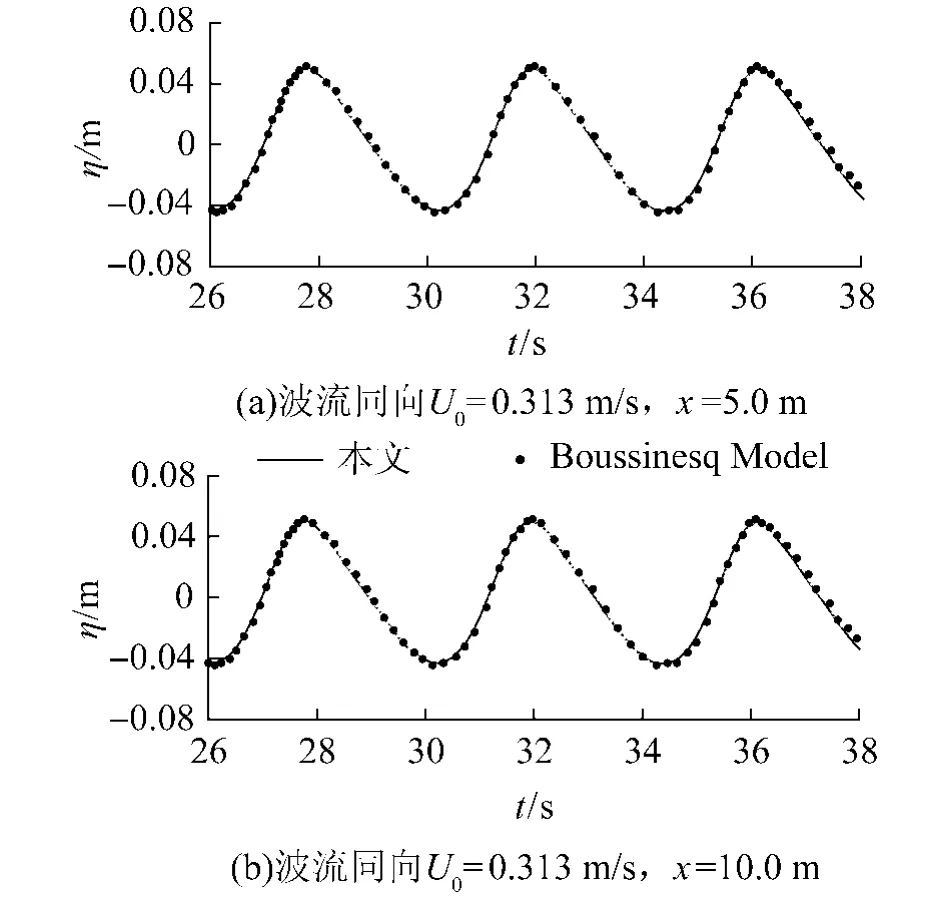
图3 波流同向时两点(x=5.0m和10.0m)处的波面时间历程及与Boussinesq模型结果对比Fig.3 Time series of non linear free surface wave with cop lanar current at x=5.0m and 10.0m and comparisons of present and Boussinesq model results.

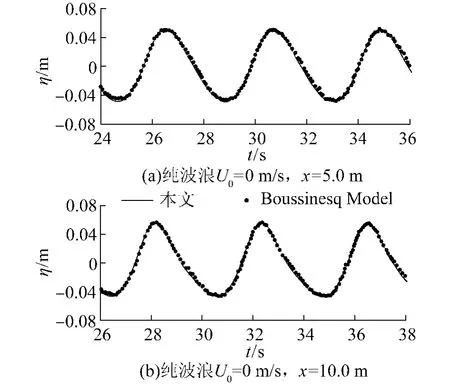
图4 无水流时两点(x=5.0m和10.0m)处的波面时间历程及与Boussinesq模型结果对比Fig.4 Time series of nonlinear free surface wave without current at x=5.0m and 10.0m and comparisons of present and Boussinesqmodel results.

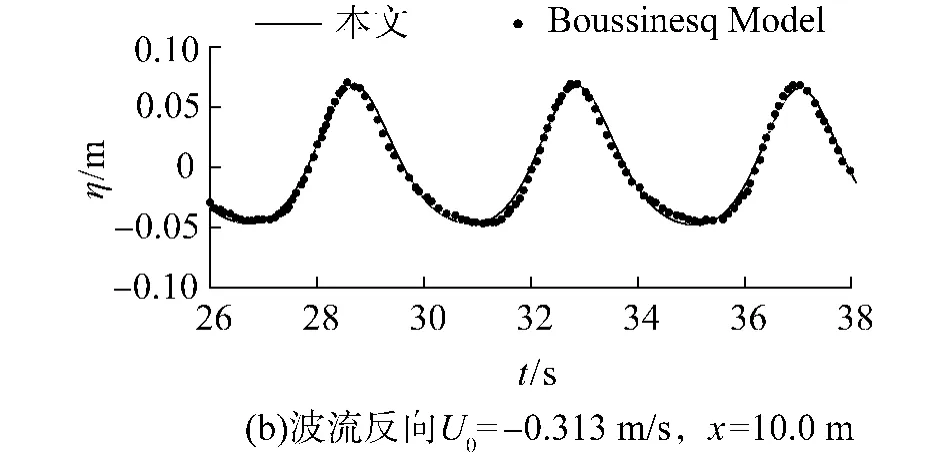
图5 波流反向时两点(x=5.0m和10.0m)处的波面时间历程及与Boussinesq模型结果对比Fig.5 Time series of nonlinear free surface wave with adverse currentat x=5.0m and 10.0m and comparisons of present and Boussinesqmodel results.

图6 x=5.0m和10.0m两点处的波面历程图Fig.6 Time histories of wave elevation at x=5.0m and 10.0m

图 7是对图 6中波面历程进行傅里叶变换得到频谱变化关系,图中横坐标通过除以波浪频率f0=1/T进行无量纲化处理.从图中可以清楚看出波流同向、纯波浪和波流反向 3种工况下非线性变化关系,以及 1阶、2阶甚至 3阶波浪的贡献.通过对比发现与图 6相同的结论,波流反向时非线性最强,纯波浪时次之,波流同向时非线性最弱.

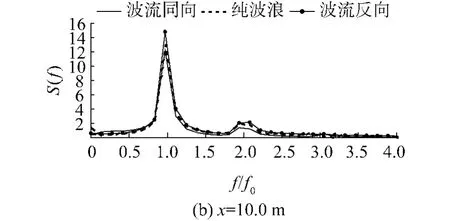
图7 x=5.0m和10.0m 3点处的频谱变化关系Fig.7 Variantion ofwave speactra with frequencey at x=5.0m、and 10.0m

接下来是保持水流速度不变,研究不同入射波幅A情况下波流同向、纯波浪和波流反向时的波面变化情况.图8是x=5.0m和10.0m两点在波流混合作用下的波峰 A*随波陡的变化情况,图中纵坐标通过除以入射波幅 A做无量纲化处理,为了进行比较,各工况下线性理论结果也在图中给出.从图中可以看出,非线性结果都随着波陡的增加而增大,但其增加的幅度波流反向情况最为明显,纯波浪次之,波流同向时最小,这与图7中非线性分析的结论是一致的.

图9是x=5.0 m和10.0m两点处的平均波高一半 A*随波陡的变化情况图,以及线性结果和非线性结果的比较.从图中可以看出与图 8相同的变化规律,但是变化幅度明显小于波峰情况,这说明波谷的起到减弱的作用.线性和非线性结果的区别也进一步说明,对于非线性较强情况,无论是波流反向还是波流同向,线性理论值都会导致很大的不准确性.

图 8 两点处不同波陡情况下波峰的变化关系Fig.8 Variation ofwave crestwith wave slope at two positions

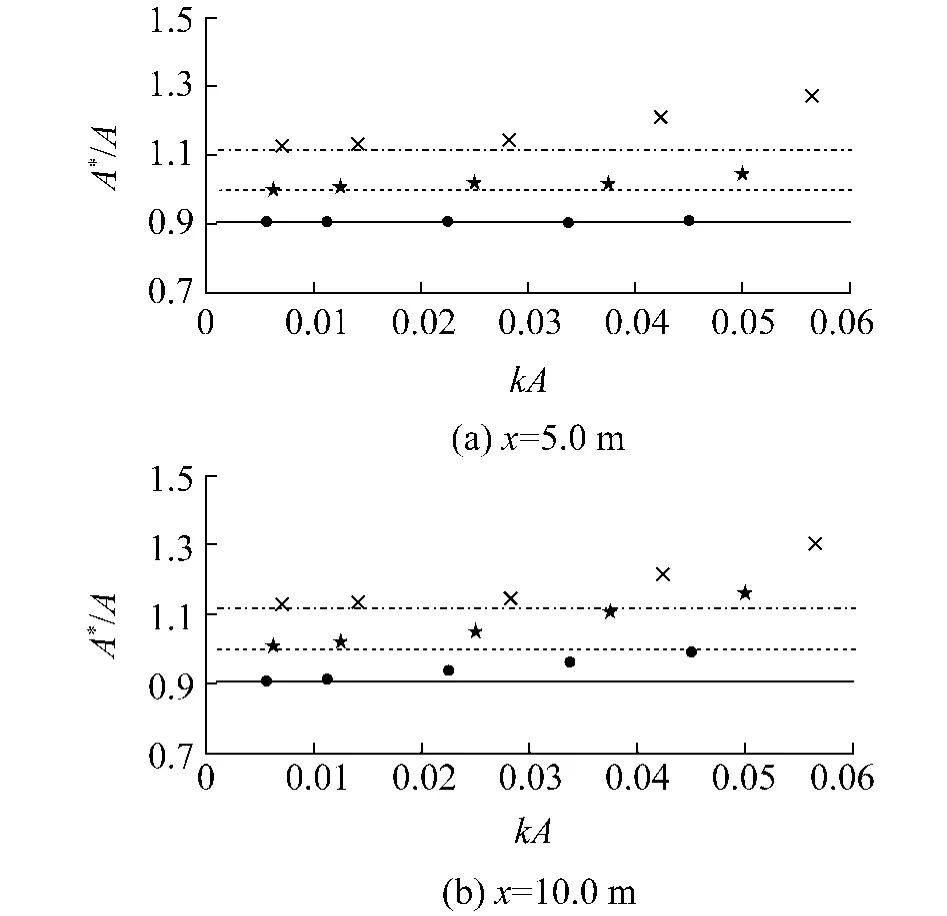
图 9 两点处不同波陡情况下平均波高一半的变化关系Fig.9 Variation ofaverge wave height with wave slope at two positions

3 结束语

本文基于时域高阶边界元方法建立波流混合作用的完全非线性数值水槽模型,并且通过不同水流条件下与Boussinesq方程模型结果对比进行验证,结果表明本文所建立数学模型可以准确模拟强非线性条件下波流混合作用问题,这是线性理论解很难做到的,特别是对于强非线性情况.研究发现,相对于纯波浪问题,波流反向作用时波峰变得更高和陡峭,波谷变得更低而平坦,也即波浪的非线性特点更加突出,对于波流同向作用则得到相反的结论,对于如本文中所研究的浅水问题,在水槽下游各点处会体现出更强的非线性特性,特别是波流反向时.本文模型的建立将有助于进一步开展波流混合与海洋工程结构物作用问题的模拟研究,为海洋工程安全设计提供参考.

[1]SCORPIO S M.Fully nonlinear ship-wave computations using amultipole accelerated,desingularizedmethod[D]. Michigan:The University ofMichigan,1997:1-106.

[2]WU G X,HU Z Z.Simulation of non linear interactions between waves and floating bodies through a finite-elementbased numerical tank[J].Proc R Soc Lond A,2004, 460:797-817.

[3]宁德志,滕斌,周斌珍,等.源造波法在三维完全非线性波浪水槽中的应用[J].大连海事大学学报,2008,34:1-5.

[4]NING D Z,TENGB,EATOCK TAYLOR R,etal.Numerical simulation ofnonlinear regular and focused waves in an infinite water-depth[J].Ocean Engineering,2008,35:887-899.

[5]BAIW,EATOCK T R.Numerical simulation of fully nonlinear regu lar and focused wave diffraction around a vertical cylinder using domain decomposition[J].Applied Ocean Research,2007,29(1-2):55-71.

[6]NOSSEN J,GRUE J,PALM E.Wave forces on 3-D floating bodies with samll forward speed[J].J Fluid Mech, 1991,242:135-160.

[7]TENG B,EATOCK TAYLORR.App lication of a higher order BEM in the calculation of wave run-up in a weak current [C]//Proceedings of the Conference ISOPE.Osaka,Japan, 1994.

[8]滕斌.深水中波浪与弱流对结构物的作用[J].海洋学报,1996,18:117-125.

TENG Bin.Wave and weak current actions on object in deep water[J].Acta Oceanologica Sinica,1996,18:117-125.

[9]ISAACSONM,NG Y T.Time-domain Second-order wave interaction with 3-D floating bodies[J].International Journal of Offshore and Polar Engineering,1995,5(3):171-179.

[10]RYU S,KIM M H,LYNETT P J.Fully nonlinear wavecurrent interactions and kinematics by a BEM based numerical wave tank[J].Computational Mechanics,2003, 32:336-346.

[11]KOOW,KIM M.Current effects on nonlinear wave body interactions by a 2-D fully non linear numerical wave tank [J].Journalof Waterway,Port,Coastaland Ocean Engineering,2007,133(2):136-146.

[12]李玉成,滕斌.波浪对海上建筑物的作用 [M].2版,北京:海洋出版社,2002:1-295.

[13]宁德志.快速多极子边界元方法在完全非线性水波问题中的应用[D].大连:大连理工大学,2005:1-166.

NING Dezhi.Application of the fastmulitpole boundary elementmethod to fu lly nonlinear water wave problems[D]. Dalian:Dalian University of Technology,2005:1-166.

[14]周斌珍,宁德志,滕斌.造波板运动造波实时模拟[J].水动力学研究与进展:A辑,2009,24(4):1-12.

ZHOU Binzhen,NING Dezhi,TENG Bin.Realtime simulaiton of waves generated by a wavemaker[J].Chinese Journalof Hydrodynamics:Ser.A,2009,24(4):1-12.

[15]KOO W,KIM M H.Current effects on non linear wavebody interactions by a 2-D fully nonlinear numerical wave tank[J].Journal of Waterway,Port,Coastal and Ocean Engineering,2007,133(2):136-146.