平面四杆机构截面参数优化设计

梁洁萍

(湖北工业大学机械工程学院,湖北 武汉 430068)

在简单弹性连杆机构设计中,应确定两类尺寸:一类是机构的几何尺寸,即对机构运动有影响的杆长、固定铰链位置尺寸;另一类是构件的截面尺寸,它对刚体运动没有影响,而只影响机构的弹性变形.弹性连杆机构的设计过程一般分为初始机构综合与弹性动力综合这两个阶段.迄今为止所提出的弹性动力综合方法都采取以某种优化理论为基础的迭代型算法.为减小高速运转的连杆机构的振动、噪声和动力消耗,宜减轻其重量.设计飞行器、舰船,限制重量尤为重要.近年来机械设计领域中最小重量优化设计方法得到迅速发展,故迄今所发表的弹性动力综合方法一般都是以重量最小化作为优化的目标[1-2].通过优化改变构件截面尺寸而获得最小重量设计的方法归为两类:一类方法是把它归结为一个有约束的非线性规划问题,另一类则借用了结构设计领域的“最佳性准则法”.前者的优点是可以处理带有各种约束的问题,变通性强;而后者则可使迭代次数大为减少[3-4].因最佳准则法能大幅度减少迭代次数,是一种效率很高的优化方法.故此采用最佳准则法通过运用有限元分析(FFA)软件对截面参数进行优化设计[5-6].

1 有限元分析法

1.1 有限元分析的典型步骤

有限元法是一种离散化的数值分析方法,其典型步骤如下[7]:1)连续体的离散化;2)选择位移模型;3)用变分原理推导单元刚度矩阵;4)集合整个离散化连续体的代数方程;5)求解位移矢量;6)由节点位移计算出单元的应变和应力.

1.2 有限元分析流程图

有限元分析流程如图1所示.

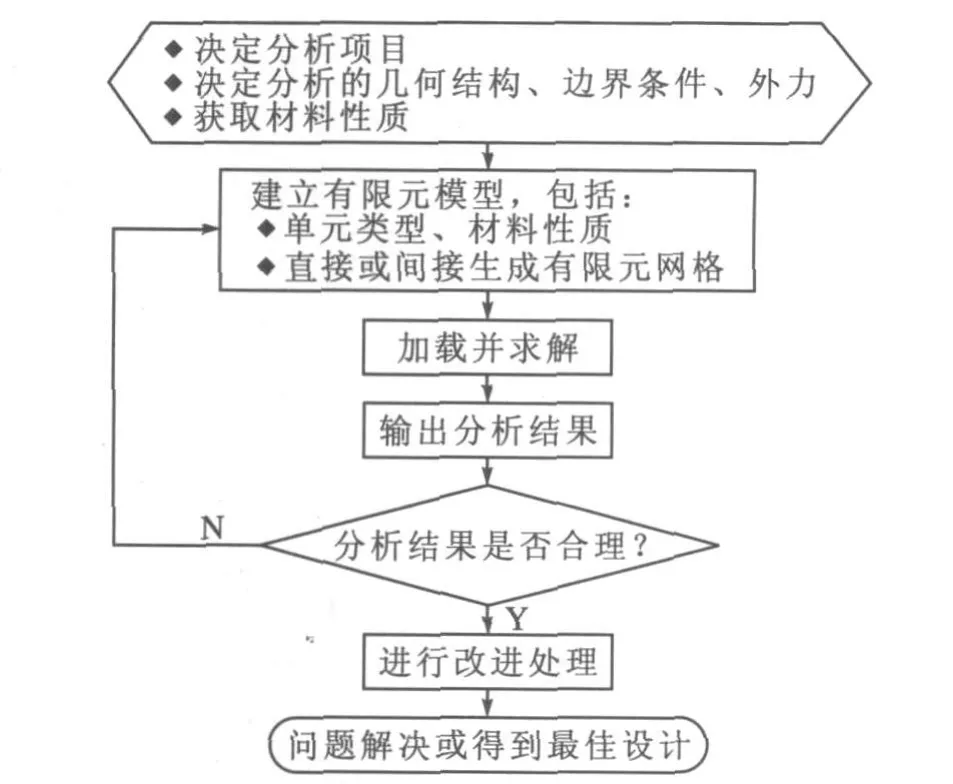
图1 有限元分析流程

2 连杆优化设计方法及实例

2.1 连杆机构优化设计

连杆机构是一种应用十分广泛的机构,如人造卫星太阳能板的展开机构,折叠伞的收放机构以及人体假肢机构等等.其中平面四连杆机构广泛应用于各种机械和仪表中.连杆机构的特点是其原动件的运动要经过一个不直接与机架相联的中间构件才能传动从动件.

利用连杆机构可以满足各种运动规律和运动轨迹的设计要求,但要设计一种能够准确实现这种要求的连杆机构却是十分繁难的,而且在多数情况下一般值能近似地得以满足.正因为如此,所以从最优化的原则角度来设计四连杆机构,使其能够最佳地满足设计要求,一直是连杆机构研究的一个重要课题.近年来对平面连杆机构的研究有了很大进展[2].优化方法和计算机辅助设计方法的应用已成为研究连杆机构的重要方法,并已相应地编制出大量的适用范围广、计算机时少、使用方便的通用软件.其中ANSYS就是运用愈来愈广泛的有限元分析软件.

如图2所示的曲柄摇杆机构是一种典型的平面四连杆机构.在该机构中,当曲柄为原动件时,可将曲柄的连续转动转变为摇杆的往复摆动.下面就以该机构为例,对平面四连杆机构进行优化设计.

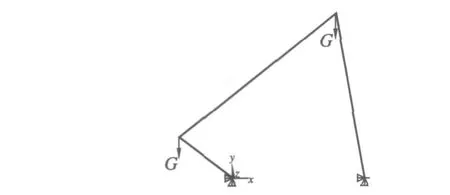
图2 平面四连杆机构分析图

2.2 最佳准则法的设计方法

2.2.1 机构的分析 首先需要说明的是,本文所提到的优化设计是建立在初始机构综合的基础之上,即是属于连杆机构设计过程中的第二阶段.因此,在分析设计之前,先假设给定该曲柄摇杆机构的具体参数为:曲柄L1=100 mm,连杆 L2=300 mm,摇杆L3=250 mm,机架L4=200 mm;杆与杆之间的铰链重G=2.7 kg;杆件密度为2.7×10-3kg/cm2;当曲柄以n=100 r/min的转速作整周回转时,摇杆随之作往复摆动.对该机构的受力分析如图2.由图可知机构平面在垂直平面上,曲柄作为原动件在n=100 r/min的转速的作用下作逆时针旋转;同时铰链作为杆与杆之间的连接体有一个向下的重力作用,其大小为G=27 N.

2.2.2 优化设计方法 应用软件(包括ANSYS软件)对平面连杆机构进行优化设计时,通常有以下几种方法,即应力约束下的最小重量设计、位移约束下的最小重量设计、频率约束下的最小重量设计[2].本文将以应力约束下的最小重量设计方法对曲柄摇杆机构进行最优化设计.

在结构设计领域,应力约束下的最小重量设计基于如下假设:最小重量设计是满应力的,即各元件中的应力均达到许用应力.实际上,满应力与最优化设计的关系并非这样简单.满应力设计并不是唯一的,而且也并不总是相应于最优化设计.但已有的数值经验表明,只要不是病态结构,大多数情况下二者相差很小[2].

2.2.3 机构应力作用下的最小重量优化 由于该曲柄摇杆机构受力与运动的单一性,现主要从静力学角度对其进行有限元分析.即选取机构运动的某一位置(如图2所示),对其进行分析计算.在分析过程中,采用了大型有限元分析软件ANSYS作为分析工具,对机构的应力、重量和面积进行一阶方法的分析计算.

对机构施加相应的约束,考虑到前述对机构的受力分析,可知该机构主要的作用力来源于铰链的重力和曲柄角速度所产生的力矩作用.在分析过程中特别要注意的是角速度的加载,(在ANSYS中需要将角速度转换为时间步长和位移的乘积).由于是静力分析,只给出机构在图示位置中各杆件的应力作用图(图3).

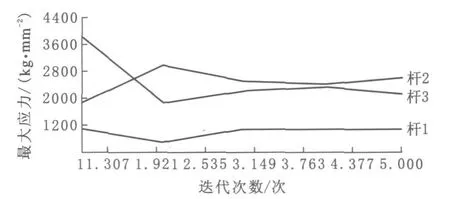
图3 载荷作用下各杆件的应力变化图

由图3可知:各杆件所受应力由开始的较大变化逐渐趋于平稳.在这种应力作用下,通过ANSYS得到机构重量变化曲线如图4所示.由图4可知:随着重量曲线的逐渐趋于平稳,不难发现在应力作用下机构的最佳重量为WT=62.14 kg.与重量曲线相对应的各杆件的截面积变化曲线如图5所示.

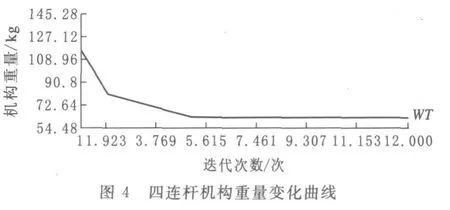
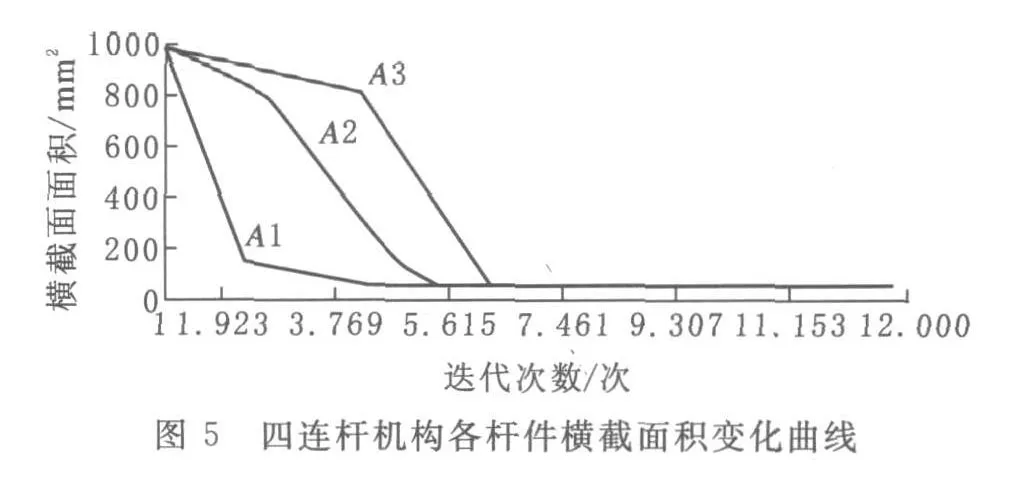
根据图4、图5可以看出:当机构重量处于最佳重量时,各杆件的横截面积相等,均为75 mm2.在以上分析过程中,将设计变量设为面积 A1、A2、A3;状态变量为杆1、杆2、杆3;目标函数为WT.

3 结论

通过上述有限元分析及优化设计结果,可以得出以下结论:

1)一般情况下进行优化设计的机构是建立在机构综合的基础之上的,在优化设计前,需要对机构的载荷与环境条件进行必要的分析;

2)在运用ANSYS软件进行优化设计时,需要设定设计变量、状态变量和目标函数,其中目标函数只能有一个;

3)平面四杆机构中各杆件所受应力在最初开始变化较大而后变化缓慢.当重量曲线变化趋于平稳时,可得到应力作用下的机构最佳重量(本实例为WT=62.14 kg),而当机构重量处于最佳值时,各杆件的横截面积相等(本实例为A1=A2=A3=75 mm2);

4)该平面四杆机构静力学分析实例及结论,为研究弹性连杆机构机电耦合的动态性能分析提供参考,为进一步的动力学分析打下基础.

[1]Caracciolo R,Trevisani A.Simultaneous Rigid-body Motion and Vibration Control of a Flexible Four-bar Linkage[J].Mechanism and Machine Theory,2001,36:221—243.

[2]张 策.弹性连杆机构的分析与设计[M].北京:机械工业出版社,1997.

[3]蔡敢为,李兆军,常平平.电动机-弹性连杆机构系统的动态方程及其响应[J].固体力学学报,2005(4):398-404.

[4]张 策.机械动力学史[M].北京:高等教育出版社,2009.

[5]梁洁萍,刘 平,王文龙,等.复杂机电系统全局耦合模型的建模[J].湘潭矿业学院学报,2002,7(4):24-27.

[6]蔡敢为,梁洁萍.三维编织复合材料构件机器人优化设计(英)[J].湘潭矿业学院学报,2002,17(2):23-28.

[7]邓凡平.ANSYS 10.0有限元分析自学手册[M].北京:北京人民邮电出版社,2007.