谐波情况下无功功率定义的分析与思考

李春燕，付志红，张 谦

（重庆大学 电气工程学院，重庆 400044）

在正弦条件下，已有很完备的功率体系［1］。但随着半导体行业和电力工业的发展，换流设备被广泛采用，大量非线性负荷增加，使系统电压、电流波形畸变，原有的正弦情况下的无功功率定义不再适用，传统的无功功率定义颇具争议。

研究非正弦条件下的功率定义问题已有很长历史，为解决非正弦条件下功率测量准确性问题，近十几年来国际电工界又重新给予了极大的重视，发表的文章分别从频域和时域等不同角度对非正弦电压电流进行了探讨［2］，提出了非正弦条件下功率、电压、电流的各种定义，但其结论并没有得到普遍承认和应用。

1 传统功率理论及其局限性

1.1 正弦电路的功率理论［1］

在正弦电路中，设电压和电流分别为：

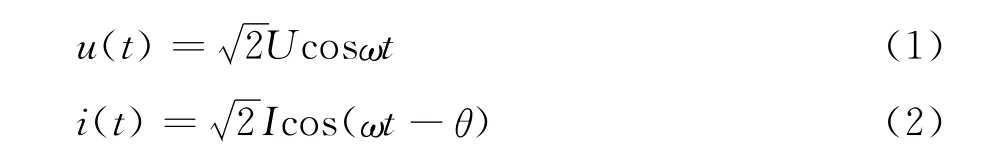
则有功功率、无功功率和视在功率分别为：

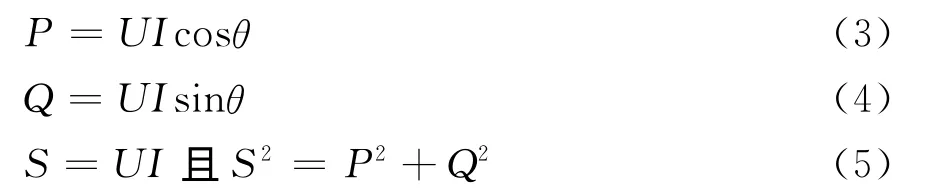
目前，几乎所有的机械式或部分电子式单相电能表都是根据上述功率理论设计的，然而这类电能表只适用于计量供电电压和电流的波形无畸变的线性负荷的电能。近年来，一些新型负荷具有程度不同的冲击性和长期非线性，不仅谐波和间谐波严重，而且谐波和间谐波存在快速变化的特性，从而导致当前出现这类单相电能表普遍少计电量的现象。

1.2 非正弦电路的传统功率理论

在非正弦电路中，电压电流分别为：

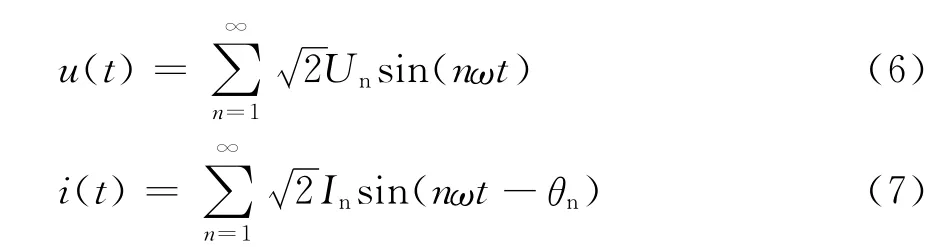
式中，Un，In分别表示n次谐波电压、电流的有效值。

有功功率、无功功率定义为：

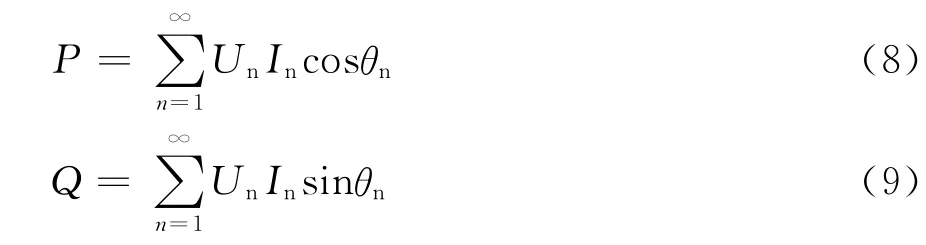
视在功率为：

显然，在非正弦情况下，S与P、Q不一定满足直角三角形关系，即S2≠P2＋Q2，所以这种功率理论并不完善，原因是在无功功率定义中没有包含不同频率电压与不同频率电流之间产生的功率交换。

针对正弦电路功率理论和传统非正弦电路功率理论的局限性，人们一直在探索新的功率理论。为了建立通用的功率理论，Budeanu（1927年）、Fryze（1932 年 ）、Shepherd 与 Zakikhani（1972 年 ）、Kuater 与 Moore（1980 年 ）、Page（1980 年 ）、Czarnecki（1983年）、Akagi（1984年）、陈祥训（1990年）、孙士乾（1991年）、杨仁刚（1992年）、李庚银（1995年）等不少国内外专家学者进行了艰苦研究，分别在频域、时域内提出了多种功率理论，下面分析几种典型的功率定义。

2 典型无功功率定义分析

2.1 频域无功功率

C.I.Budeanu在1927年提出的非正弦条件下的频域无功功率定义，由于被ANSI／IEEE标准所采纳，在电工界广为流传［3］。其定义如下：

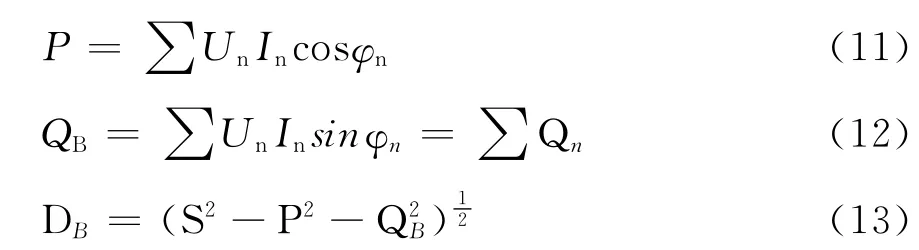
式中QB称为无功功率，为每次谐波分量无功的总和；DB称为畸变功率；n为谐波次数；Un、In分别为n次谐波电压、电流的有效值；φn为n次谐波电压、电流间的夹角。

QB简单地把各次谐波的值相加，但每次谐波分量都含有不同的频率，且可能有不同的相角，因此QB并不能表达出整个瞬时功率的可逆分量。虽然每次谐波对应的Qn都有其清晰的物理意义，但它们之和QB却完全失去了其代表的物理意义。特别是当电源和负载之间存在着能量交换，Qn为非零时，而QB却可能为零。这是QB公式在物理概念上的主要缺陷，也是Budeanu传统无功功率争议的地方。为平衡视在功率、有功功率和无功功率的关系而引入的畸变功率只是一个数学量，没有任何物理意义。

2.2 时域无功功率

1932年，Fryze对无功电流和无功功率进行了时域分析［4］，即把电流按照电压波形分解为有功电流ip和无功电流iq，其中ip的波形与电压u完全一致，iq、ip正交，其定义如下：

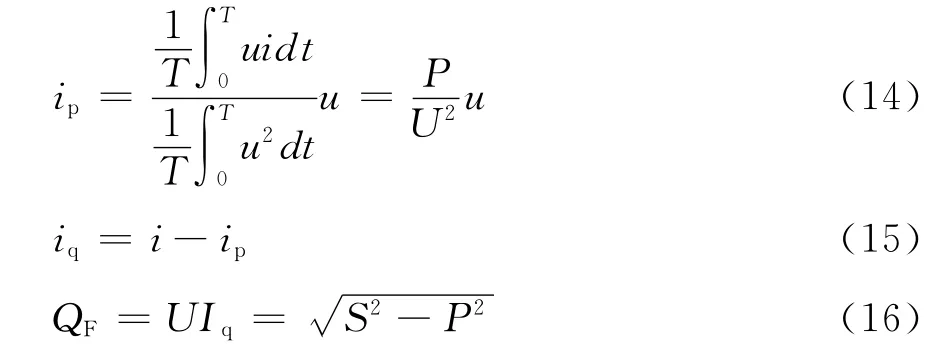
式中ip、iq分别为有功电 流和无功电 流；Ip、Iq分别为ip、iq的有效值；U 为电压有效值；S、P、QF分别为视在功率、有功功率和无功功率。

该定义的优点是可以不对电压、电流波形进行傅立叶分析就可以检测到这三种功率，QF可以直接通过视在功率S和有功功率P来计算。但QF实际上不是无功功率，而是一个新的全功率，因此，它没有如正弦波形下功率定义那样明确的物理定义，不能提供能改善功率因数至何种程度的信息，不能反映负载的情况。

2.3 Czanecki无功功率

1983年，Czanecki批驳了Budeanu的关于无功功率QB和畸变功率DB的错误观念，提出了具有清晰物理意义的电流与功率的正交分解［5，6］。

Czanecki无功理论对谐波和无功功率辨析问题的解决起了很大的促进作用，结合时域与频域分析方法，把电流分解成有功电流ia、无功电流ir、散布电流is。

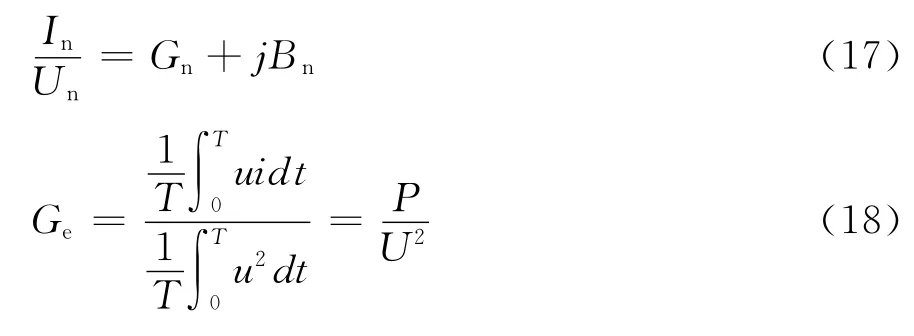
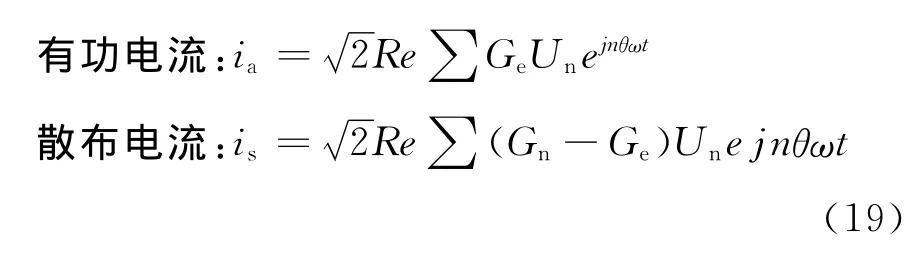
并且ia、is、ir、ig四个量两两正交。

无功功率定义为：

式中U、Ir为电压u、无功电流ir的有效值。

此无功功率定义比Fryze与Shepherd and Zakikhani更加详细。1991年，Czarncki曾对单相非正弦系统提出了一个使其得到完全补偿的设计计算方法。在理论上，假定Gn为常数，这个计算方法是成立的，用这种方法计算出来的LC串并联电路就可以很好地补偿无功功率。在工程实践上，因为Gn为常数的负荷情况比较少，所以某些方面还需要进一步改进。

综上可见，频域功率定义，就是将各次谐波的功率相加作为总功率。频域定义保留了各频谱分量的信息，但在实现时计算量很大，无法实时测量，对于补偿也显得无能为力。时域功率定义在实际应用中可以实现补偿电流的实时计算，但它也丢掉了信息的各次频率分量的信息，对于信号的分解和能量现象的进一步分析和电网中谐波源的确定等依据信号频谱来识别的研究无能为力。

2.4 瞬时无功功率

1983年，H.AKagi（赤木泰文）等人完全从补偿的角度出发在三相电路中引入瞬时无功的概念，提出瞬时无功功率的定义和电流分解的方法和理论［7－9］。

设三相电路的瞬时电压和瞬时电流分别为uA，uB，uC，iA，iB，iC，将它们分别变换到两两正交的α－β坐标系上（Park变换），可得到两相瞬时电压uα，uβ和iα，iβ，即：

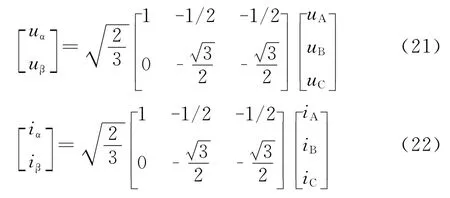
则瞬时有功和无功功率分别为：

该定义通过Park变换和反变换计算出需补偿的电流，通过补偿来减少能量传输损耗，解决了谐波和无功功率的瞬时检测及不用储能元件实现谐波和无功补偿问题，对谐波和无功补偿装置的研究和开发作出了很大贡献。但该理论只适用于三相三线制电路问题，不能很好的处理零序分量。

2.5 任意周期电压电流的无功功率［10］

将电压、电流展开为傅立叶级数：

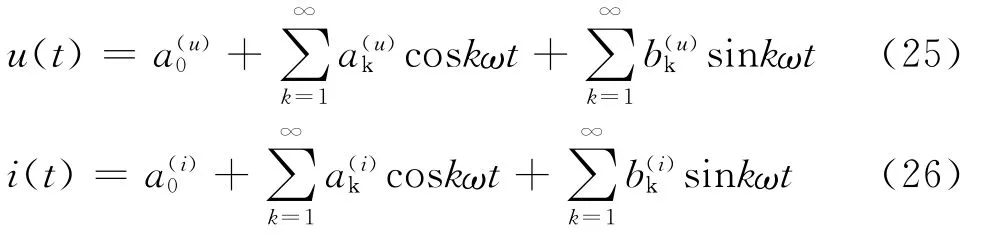
定义功率矩阵为：

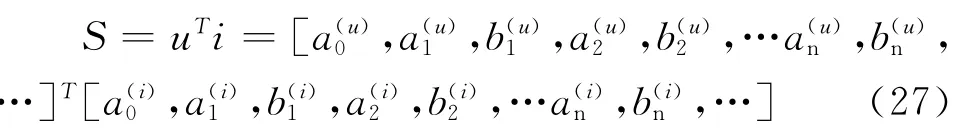
其中，主对角线上的元素对应的是同坐标轴上的电压、电流形成的有功功率。从而，有功功率平均值定义为功率矩阵S主对角线上所有元素和的1／2。

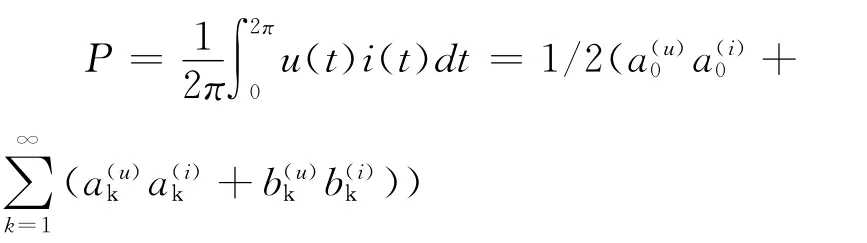
而非主对角线上的元素就是不同坐标轴上的电压、电流形成的电功率，代表的是以电功率、磁功率或电磁功率的形式进行的能量交换，相应的功率为无功功率。该定义指出无功功率各分量应由无功功率电流、电压偶对来描述，而不是由传统的单独的无功电流（电压）分量等术语描述。

3 结论

目前各种无功功率理论都存在各自的局限性。有的适用于谐波和无功功率的辨识，有的适用于谐波和无功功率的补偿和抑制，有的适用于仪表测量和电能收费和管理。

综上，无功功率理论应具有以下特点：① 应明确功率体系中各功率分量物理意义，能清楚地解释各种功率现象，并在某种程度上与传统功率理论相同。②有利于对谐波源和无功功率的辨识和分析及对谐波和三相不平衡功率本质的理解。③ 有利于对谐波和无功功率进行补偿和抑制，能为其提供理论依据。④ 定义的各功率分量能够被精确测量，有利于有关谐波和无功功率的监测、管理和收费。

［1］周守昌.电路原理（第二版）［M］，高等教育出版社，2004

［2］王学伟，高朝.畸变波形下功率定义问题的探讨［J］，电网技术，2004，28（23）：17－21

［3］P.S.Filipski，M.D.Cox.Discussion on power definitions contained in the IEEE dictionary［J］，EEE Transactions on Power Delivery，1994，9（3）：1237－1244

［4］Chester H.Page.Reactive Power in Nonsinusoidal Situations［J］，IEEE transactions on instrumentation and measurement，1980，29（4）：420－423

［5］Czarnechi L S.Considerations on the reactive power in non－sinusoidal situations［J］，IEEE transactions on instrumentation and measurement，1985，34（3）：399－404

［6］L.S.Czarnecki.Distortion power in systems with nonsinusoidal voltage［J］，IEE proceedings－B，1992，139（3）：276－280

［7］Akagi H，Kanazawa Y，Nabae A.Generalized theory of the instantaneous reactive power in three－phase circuits［J］，international conference on power electronics，Tokyo，1983

［8］王茂海，刘会金.通用瞬时功率定义及广义谐波理论［J］，中国电机工程学报，2001，21（9）：68－73

［9］薛永端，徐丙垠.基于Hilbert变换的非正弦电路无功及瞬时无功功率定义［J］，电力系统自动化，2004，28（12）：35－39

［10］陈允平，彭 辉，樊友平.基于任意周期电压电流的无功功率定义及其数学模型［J］，中国电机工程学报，2006，26（4）：106－112