黏性土土压力计算

刘 敏,王世强

(黑龙江省龙建路桥第四工程有限公司)

1 等效内摩阻角法

这种方法在设计黏性土填料的挡土墙时,将内摩阻角曲单位黏聚力c,换算成较实有 φ值大的“等效内摩阻角”φD来代替,然后按砂性土的库仑土压力公式计算土压力。

φD值可以按换算前后土的抗剪强度相等或土压力相等的原则来计算,一般是把黏性土的内摩阻角值增大 5°～10°,或取等效内摩阻角 φD为 30°～35°。

由于影响土压力数值的因素是多方面的,包括墙高、墙型、墙后填料的表面以及荷载的情况等,不可能用上述方法为之确定一个固定的换算关系或固定的换算值。用上述方法换算的内摩阻角只与某一特定的墙高相适应,一般对于矮墙偏于安全,对于高墙则偏于危险。因此,在设计高墙时,应按墙高酌情降低φD值。最好按实测的 c、φ值,用力多边形法计算黏性土的主动土压力。

2 力多边形法(数解法)

当挡土墙向外有足够位移时,黏性土层顶面将出现拉应力,使土层产生竖向裂缝,裂缝从表面向下延伸到拉应力趋于零处。裂缝深度可以按式(1)计算

式中:c为填料的单位黏聚力,kPa。

在垂直裂缝区hc范围内,竖直面上的侧压力等于零,因此在此范围内不计土压力。

根据库仑理论,假设破裂面为一平面,沿破裂面上土的抗剪强度由土的内摩阻力σtanφ黏聚力c组成。墙背和土之间的黏聚力c′,由于影响因素很多,为简化计算,可以忽略不计,偏于安全。

现以路堤墙后破裂面交于荷载内的情况为例,介绍力多边形法计算黏性土压力公式的推导。

路堤式挡土墙,填土表面有局部荷载,裂缝深度假定从荷载作用面以下产生。BD为破裂面,破裂棱体为 ABDEFMN。在主动极限平衡状态下,棱体在自重G、墙背反力Ea、破裂面反力R和破裂面黏聚力四个力的作用下保持静力平衡,这 4个力构成力矢量多边形。从力多边形可知,作用于墙背的主动土压力为

式中:E′为当c=0时的土压力,根据式(1)得

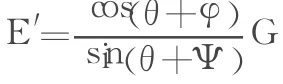
G为棱体ABDEFMN的自重,在边界条件下

其中

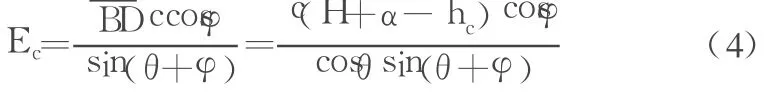
式(1)中的Ec是由于黏聚力

将上式整理化简即可得到破裂角θ的计算公式:

其中

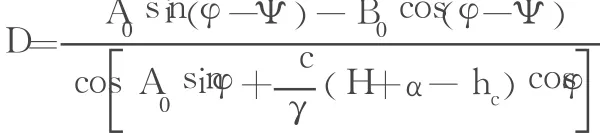
将 θ代入Ea的表达式,即可求得主动土压力 Ea。