具有阶段结构和捕食者扩散的捕食系统研究
马小箭
(山西大同大学数学与计算机科学学院,山西大同 037009)
文献[1]研究了两种群均具有阶段结构的非自治捕食系统,其中食饵可在两缀块迁移,但是考虑捕食者可在两缀块迁移的自治系统还不多,在文中,我们将讨论下面的捕食模型:
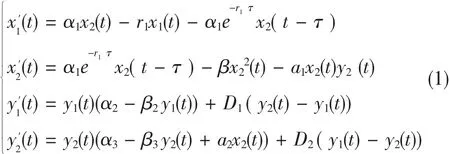
其中x1(t),x2(t)分别表示时刻食饵群幼年和成年的密度.y1(t),y2(t)分别表示t时刻两捕食种群在缀块1和缀块 2的密度.α1,α2,α3,β1,β2,β3,r1,a1,a2,D1,D2,均是正常数.
我们对模型做如下假设:
(H1)食饵种群:r1是内禀增长率,β1是logistic增长系数.a1是捕食率,α1е-r1τx2(t- τ )代表在 t- τ时刻出生的幼年食饵种群并且转化成成年种群的数量.(H2)捕食种群:a1,a2分别是捕食者在两缀块上的内禀增长率.β2,β3是logistic增长系数.a2是捕食者的转化率,D1,D2,是扩散系数.
系统(1)的初始条件是:

为了便于研究,我们定义:

根据初始条件的连续性要求:
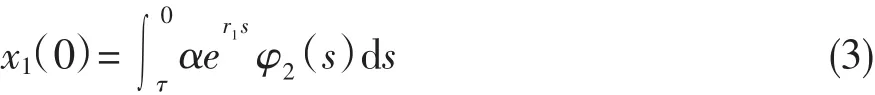
引理1系统(1)具有初始条件(2),(3)的解都是正的.
证明 我们先来证明,当 t>0时,都有 x2(t)>0.若不成立,则存在一个t0>0使得x2(t0)=0.因为x2(t)>0,t∈[-τ,0],所以 t0>0.定义 t*=inf{t>0 ∶x2(t)=0}.因此由系统(1)可以得到:

但由t*的定义,可以得到这与上式矛盾,因此t>0时,x2(t)>0.当t∈[0,τ]时,由系统(1)的第一个方程,得

我们构造一辅助方程
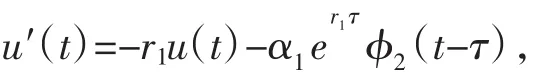
初始条件为:u(0)=x1(0),所以有
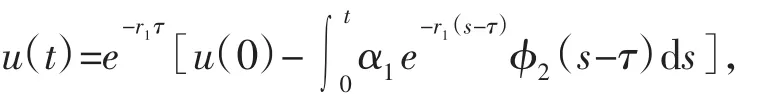
综合(3)得

因为 u(t)是严格递减的,所以在 t∈[0,τ]时,有 u(t)>u(τ)=0.由比较定理知,当t∈[0,τ]时,有x1(t)>u(τ)>0.类似文献[3]的方法,可以证明,当 nτ≤t≤(n+1)τ,n=0,1,2,…,x1(t)>0.
由系统(1)的第三,四个方程得:
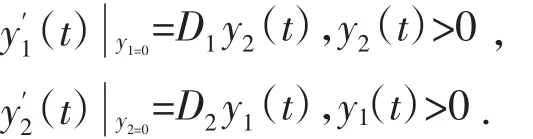
因此我们得到了对所有t>0时都有xi(t)>0,yi(t)>0(i=1,2).
引理2考虑方程
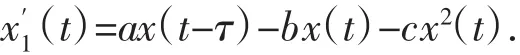
其中 a,b,c是正常数 x(t)>0,t∈[-τ,0].我们有
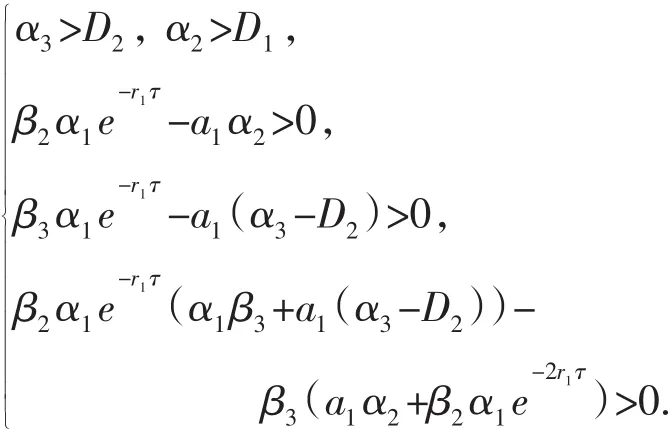
则系统(1)是一致持久性的.
证明假设(x1(t),x2(t),y1(t),y2(t)),是系统(1)具有初始条件的任意正解.
定义V(t)=max{y1(t),y2(t)},使用类似于文[2]引理3.2的证明,我们得到
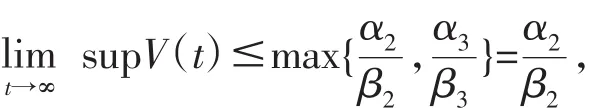
所以对任意的 ε>0,存在 T1>0,使得当 t>T1时,

又由系统(1)的第三,四个方程得
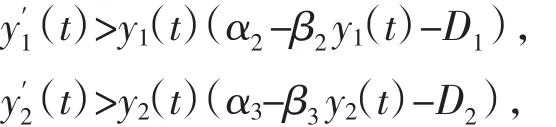
根据比较定理得
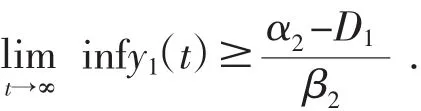
因此,对任意的 ε>0,存在 T2>T1,使得当 t>T2时

类似的
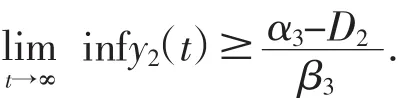
因此,对任意的 ε>0,存在 T3>T2,使得当 t>T3时
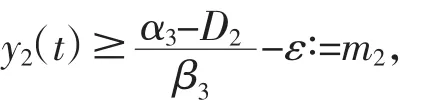
由系统(1)的第二个方程得
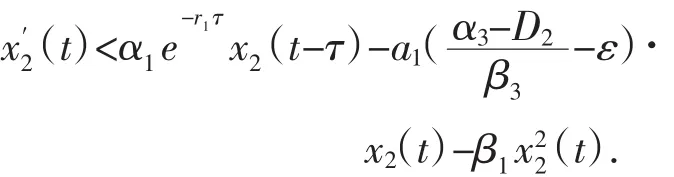
我们构造一辅助方程
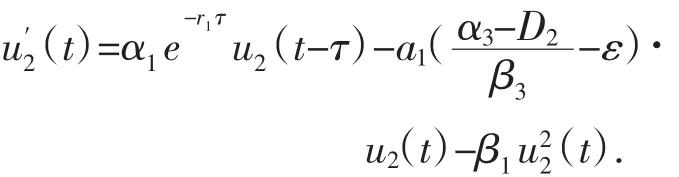
由引理(2)及比较定理得

因此对充分小的ε>0,存在T4>T3,使得当t>T4时,
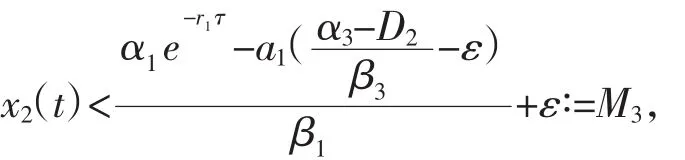
类似的,由
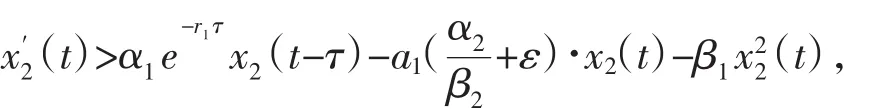
得

因此对充分小的 ε>0,存在 T5>T4,使得当 t>T5时,

由系统(1)的第一个方程得
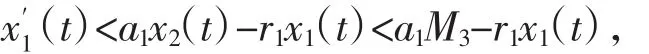
即
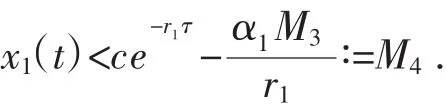
又因为

我们令
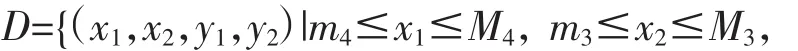
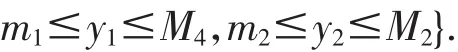
那么D就是在R4+上的一个有界紧区域,系统 (1)具有初始条件(2)的解最终都进入并保持在D内,所以系统(1)是一致持久的.
[1]Ruixu Chaplain M A J,Davidosn F A.Persistence and periodicity of a delayed tatio-stat[J].Theoretical Population Biology,1993,44:203-204.
[2]Xu R,Chen L S.persistence and stability for a two-species ratio-depedent predator-prey system with time delay in a two-patch environment[J].comput math Appl,2000,40:577-588.
[3]Tognetti K.The two stage stochastic model[J].Math Biosi,1975,25:195-204.
[4]康淑瑰.时滞差分方程正周期解得存在性[J].山西大同大学学报:自然科学版,2009,25(2):6-7.
[5]马知恩.种群生态学的数学建模与研究[M].合肥:安徽教育出版社,1996.
- 山西大同大学学报(自然科学版)的其它文章
- 中国古代律学及其文化意义初探

