具变号系数的四阶非线性变时滞微分方程的振动性
郭 芳,朱红霞 ,韩效宥
(1.山西大同大学数学与计算机科学学院,山西大同 037009;2.河北廊坊师范学院数学与信息科学学院,河北廊坊 065000;3.北方工业大学理学院,北京100144)
对于不变系数的高阶变时滞微分方程解的振动性研究已经有很多研究成果[1-3].2007年,韩效宥和朱红霞“用一种新的方法研究了具变符号振动因子的二阶非线性时滞微分方程解的振动性[4]”.同时对二阶非线性变时滞微分方程解的振动性也做了研究[5].从此开始了变符号振动因子微分方程的研究.此后2008年,韩效宥又研究了具变符号振动因子的四阶非线性微分方程解的振动性[6-7],结合上述几篇文章的研究,本文研究具变符号振动因子的四阶非线性变时滞微分方程解的振动性,并得到了该方程振动的充分条件.
本文研究方程:.
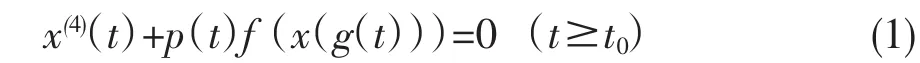
其中:p(t),g(t)∈C([t0,+∞],R),
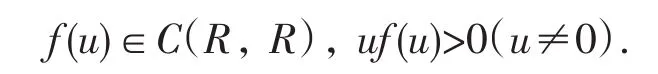
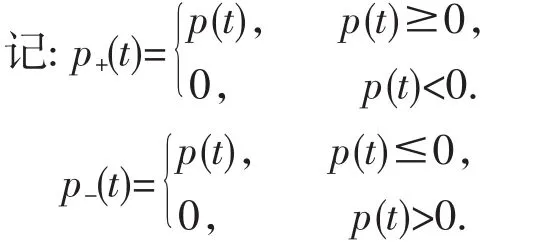
则:方程(1)可写为:
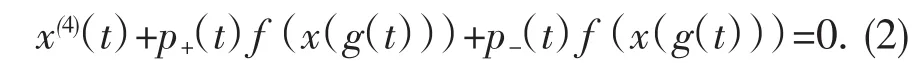
定义:称方程(1)的解是振动的,是指它有任意大的零点且非最终恒为零;称方程(1)是振动的.是指它的所有解是振动的.
1 主要结果
引理1若方程(1)满足下列条件:
(a)存在常数l1,l2,使:
(c)p-(t)≥-e-t4;
(d)存在常数 σ>0,使 g(t)∈C([t0,+∞],R)满足:t-σ≤g(t)≤t且g′(t)>0.
则:当x(t)为方程(1)的非振动最终正解时,存在常数 λ0,λ1,λ2,λ3使得当x(t)为方程(1)的非振动最终负解时,存在常数λ使得:
证明:假设方程(1)是不振动的,则方程至少存在一个最终正解或最终负解.不妨假设方程存在一最终正解 x(t),则存在 t1≥t0,当 t≥t1时,有 x(t)>0且 x(g(t))>0(最终负解的情形可类似证明).记:
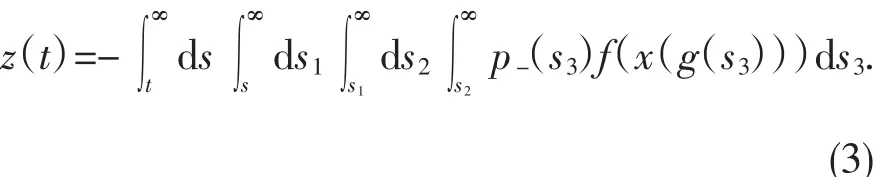
(b)
则:z(4)(t)=-p-(t)f(x(g(t))),因此
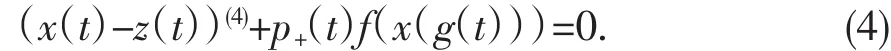
对方程(2)从t1到t进行4次积分,得
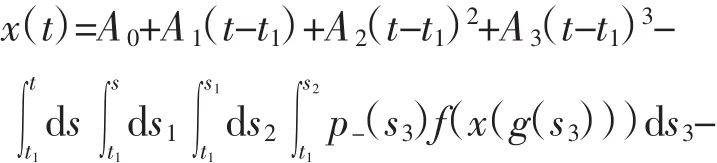
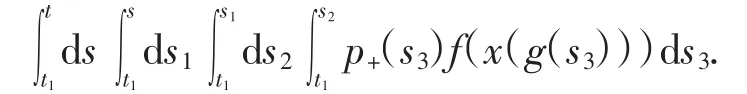
其中:A0=x(t1),A1=x′(t1)令
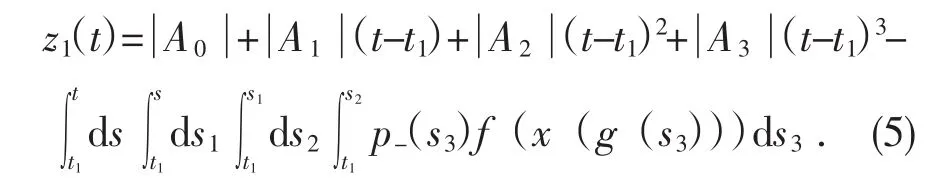
所以存在t2≥t1,当t≥t2时,有x(t)≤z1(t),
且z1(4)(t)=-p-(t)f(x(g(t))),因此当 t≥t2时,有x(g(t))≤z1(g(t))≤z1(t).
因为z1(4)(t)=-p-(t)f(x(g(t))),所以有
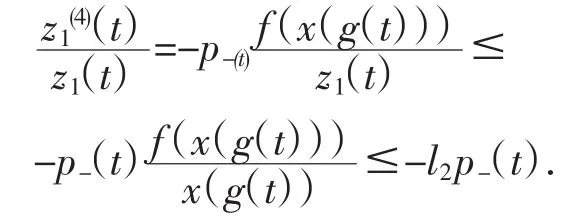
对上述不等式两边积分4次得
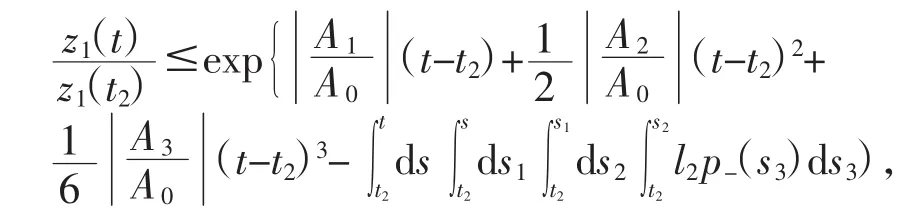
进行化简整理得
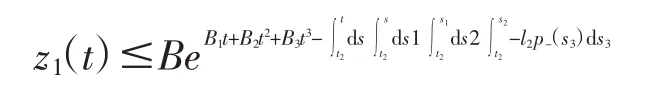
又因为p-(t)≥-e-t4,记为常数),
因为
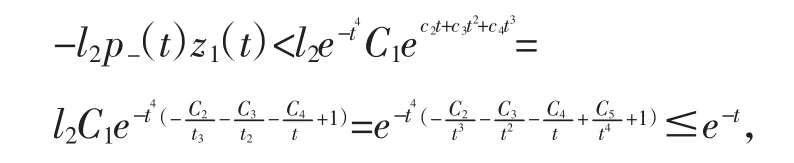
又有z(4)(t)=-p-(t)f(x(g(t)))<-l2p-(t)x(g(t))<-l2p-(t)z1(t),
所以存在t3≥t2,当t≥t3时,有z(4)(t)≤e-t(t充分大).
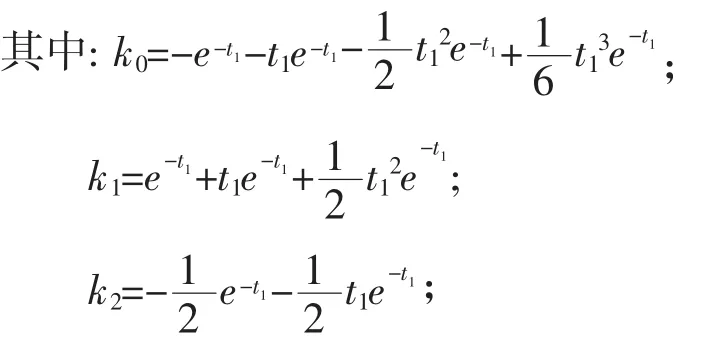
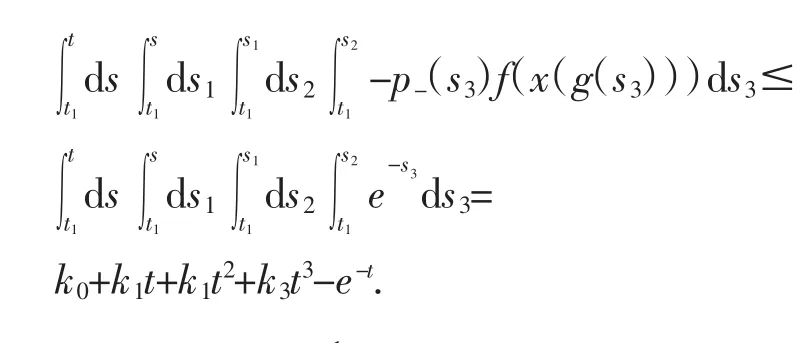
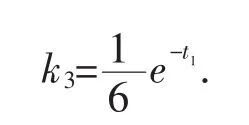
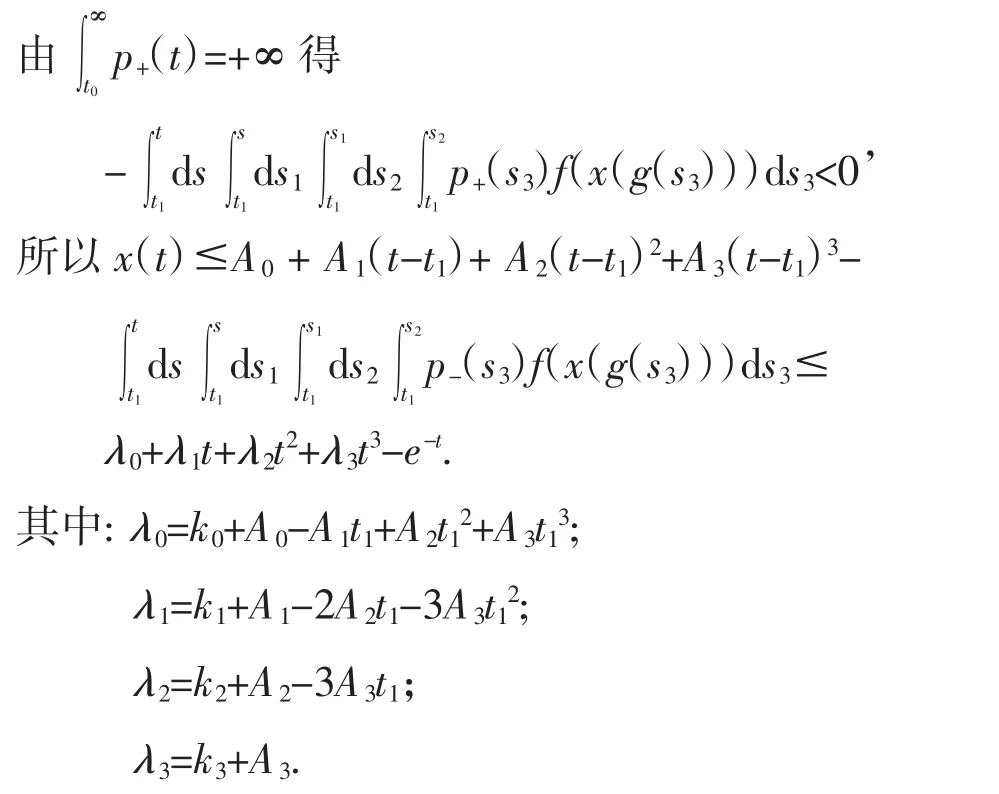
引理2 若方程(1)满足上述(a)(c)和(d)条件,并且满足下面条件时:
(e)对于任意N,存在b>a≥N,使得对于 t∈[a,b],有p-(t)≡0,其中则当方程(1)有非振动解 x(t)时,和y′(t),y′(g(t)),y‴(t)最终均不变符号.
证明:因为(x(t)-z(t))(4)=-p+(t)f(x(g(t)))≤0,且不最终为零.因此当 x(t)>0 时,有 x(t)-z(t),(x(t)-z(t))′,(x(t)-z(t))″,(x(t)-z(t))‴ 最终单调不变号,下面证明(x(t)-z(t)最终大于零.分以下两种情况来证:
下面证明x(t)-z1(t)最终大于零,分两种情况来证.
第一种情况:当 t′k>ak+τ时,
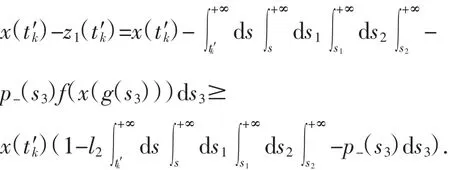
易见存在N,当k≥N时,有x(t′k)-z1(t′k)>0,即x(t)-z1(t)最终大于零.
第二种情况:当 ak≤t′k<ak+τ时,
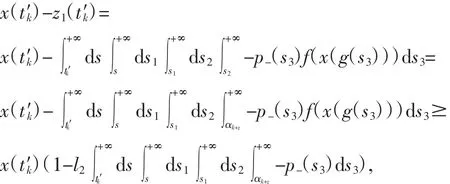
故x(t′k)-z1(t′k)>0,即x(t)-z1(t)最终大于零.
综上所述,存在t4≥t3,当t≥t4时,x(t)-z1(t)>0,x(g(t))-z1(g(t))>0.由条件(a)得
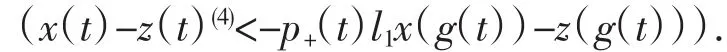
令y(t)=x(t)-z(t),则y(4)(t)<-l1p+(t)y(g(t))<0.
若y(3)(t)<c<0,两边从t4到t进行3次积分得

若y(3)(t)>c>0,两边从t4到t进行2次积分得
所以若 y″(t)>0,则有 y′(t)>0;若 y(t)″<0,则有y′(t)>0,(否则,y>0,与y>0矛盾)
综上,当t≥t4时,有y‴(t)>0,y′(t)>0,y′(g(t))>0.
2 定理及其证明
定理 若方程(1)满足上述(a),(b),(c),(d),(e)条件,则方程(1)是振动的.
证明:假设方程(1)是不振动的,则不妨假设方程存在一最终正解 x(t),且 x(g(t))>0.(最终负解的情形可类似证明).由引理2知:y(4)(t)<-l1p+(t)y(g(t))<0,且有y‴(t)>0,y′(t)>0,y′(g(t))>0.
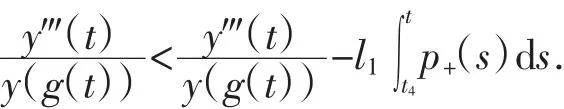
3 结论
当方程x(4)(t)+p(t)f(x(g(t)))=0满足上述定理中的条件时,此方程的解是振动的.
[1]邹杰涛,郭金花,侯艳红,等.某类二阶非线性时滞微分方程的振动性[J].数学的实践与认识,2007,37(05):142-146.
[2]李宏飞,王志斌.变系数变时滞高阶非线性中立型方程的振动性[J].工程数学学报,2000,17(3):121-124.
[3]杨军,李静,王春艳.变时滞高阶非线性中立型微分方程的解的振动性、渐进性及分类[J].纯粹数学与应用数学,2005,21(2):118-121.
[4]朱红霞.几类二阶时滞微分方程的振动性研究[D].北京:北方工业大学,2007.
[5]韩效宥,石燕霞,庄需芹.某类系数变号的二阶非线性变时滞微分方程的振动性[J].数学的实践与认识,2007,37(15):155-159.
[6]韩效宥,郭芳,韩少伟,等.具变号系数的四阶非线性微分方程的振动性[J].数学的实践与认识,2008,38(11):168-172.
[7]郭芳,朱红霞,韩效宥.具变号系数的四阶非线性时滞微分方程的振动性[J].北方工业大学学报,2009,21(03):37-40.

