高层建筑加强层粘滞阻尼系统的优化分析＊

汪志昊,陈政清

(湖南大学土木工程学院,湖南长沙 410082)

框架核心筒结构在高层建筑中被广泛应用[1],其中又有部分结构设有一个或若干个结构加强层.所谓加强层,即从核心筒或剪力墙外伸并与外围框架柱连接在一起的具有较大刚度的水平构件.在水平荷载作用下,由于加强层的存在,使得与加强层相连的两侧外柱分别沿轴向受拉和受压,形成的反力矩抵消了由外界水平荷载产生的部分倾覆力矩,同时减小了结构侧移[2-6].国内外已有较多采用加强层的高层建筑工程实例,如200 m高的广州国际大厦就设置了3个桁式加强层[5].

虽然加强层的设置可以有效减小高层建筑在水平荷载下的侧向位移,但同时在加强层的位置也形成了刚度突变,加强层与外框架柱连接节点的刚性对结构的内力与变形影响很大[6],对结构抗震存在不利因素.附加液体粘滞阻尼器可以有效降低结构在动力载荷作用下的反应,减小结构设计对固有阻尼的依赖.为此,周云等[7]提出将加强层桁架中的支撑用耗能部件(支撑+阻尼器)代替,形成耗能减振层.此外,Jeremiah最早提出将加强层与外围框架柱断开,利用加强层与外围框架柱间相对大的位移差,布设竖向粘滞阻尼器的创新思想[8].在此基础上,Smith等提出了面向工程实践的加强层阻尼系统,分析表明,该系统可以大幅提高结构的模态阻尼比,从而有效降低了在风荷载作用下的动力响应,并已成功应用到菲律宾某超高层住宅楼的设计中[9-10].

本文以设置一个加强层阻尼系统的高层建筑为例,采用简化的力学模型,首先通过单自由度模型,定性地了解这一新型耗能减振系统,接着采用假定振型法和有限单元法得到多自由度模型,基于模态阻尼比,优化了线性粘滞阻尼器的阻尼系数,最后对某高层建筑加强层阻尼系统的减震效果进行了数值仿真分析.

1 计算简图

对于框架-核心筒超高层结构体系,由于核心筒体的抗侧刚度远大于外框架的抗侧刚度,从而使水平剪力中的绝大部分由内筒来承担;另一方面,在水平力的作用下,核心筒体的侧向变形类似于悬臂梁,呈弯曲型[3].因此特引入以下假定,以得到简化计算模型:核心筒或剪力墙承担全部水平荷载,并简化为等截面欧拉-伯努利悬臂梁;加强层视为刚度无穷大而质量忽略不计的刚臂;结构框架柱轴向刚度足够大,忽略轴向变形;结构固有模态阻尼为常数.从而得到如图1所示的计算简图,其中ρ A,EI,h,α h,ε,ζ,Cd分别表示核心筒的单位长度质量、抗弯刚度、高度、加强层的位置、半宽(偏心距)、结构的固有模态阻尼比和线性粘滞阻尼器的阻尼系数.

2 计算模型

2.1 单自由度模型

根据GALERKIN方法,核心筒侧向位移响应w(x,t)可以表示为:

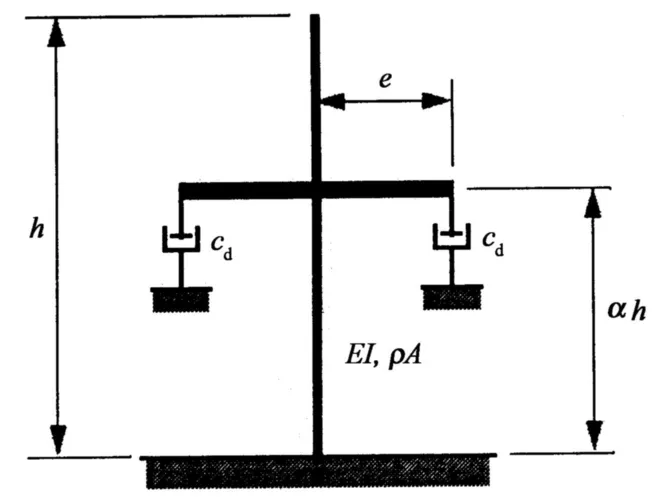
图1 耗能减振系统计算简图Fig.1 The simplified calculation diagram of energy dissipation system

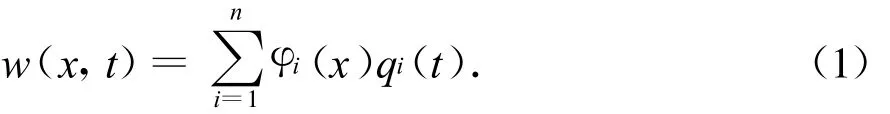
式中:qi(t)为第i阶振型独立广义坐标;φi(x)为第i阶振型函数,且满足边界条件φi(0)=0,φ′i(0)=0.为得到单自由度模型,只假定一阶振型,即w(x,t)=φ(x)q(t),且满足边界条件φ(0)=0,φ′(0)=0.由虚位移原理可知,对任意可能的虚位移δ w(x,t),系统实际力与惯性力所做的虚功δ W实际力,δ W惯性力之和为零,即:

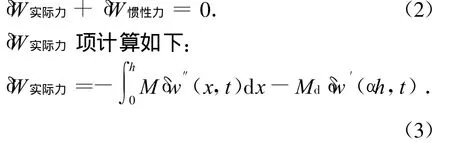
其中:δ

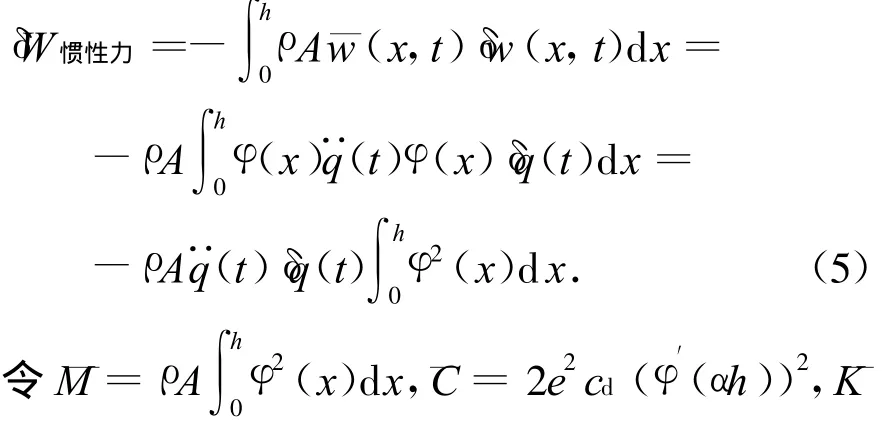
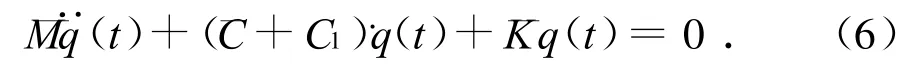
从等效模态参数的定义可以看出,由于偏心距e的平方项效应,结构的等效模态阻尼得到明显的放大,并且其还与转角振型函数在加强层处的取值有很大关系.简单来看,似乎阻尼系数越大,结构的模态阻尼也就越大.事实上,当阻尼无限大时,加强层就变成了与外围框架柱直接刚性相连,根本起不到耗能减振的作用.因此,通过单自由度模型,只能定性地了解这一新型耗能减振系统,定量的分析必须采用多自由度模型.

2.2 基于假定振型法的多自由度模型

Johnson采用假定振型法求解斜拉索最优阻尼系数问题时发现,第一阶振型若选用阻尼力作用下的拉索静力变形曲线,可以加快求解的收敛速度[11].因此,对于加强层阻尼系统,一阶振型尝试采用在加强层位置处施加外力偶下的核心筒侧移变形曲线,无量纲化后得:

其余振型采用幂函数表示:

设悬臂梁阻尼系统的广义坐标运动方程的矩阵形式为:

其中:Cd,Ci分别表示结构的附加阻尼矩阵与固有阻尼矩阵.限于篇幅,结构的质量矩阵及刚度矩阵推导从略,直接给出如下:

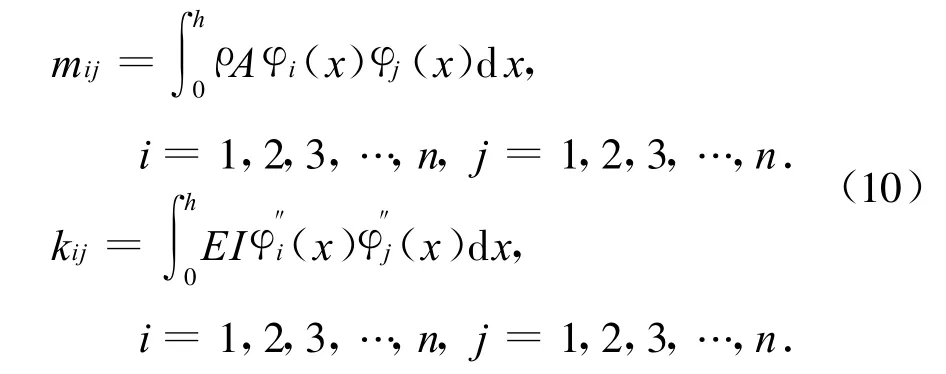
由于系统中阻尼矩阵比较复杂,基于虚位移原理,下面给出简单的推导过程.由式(1),易得到核心筒的转角响应:

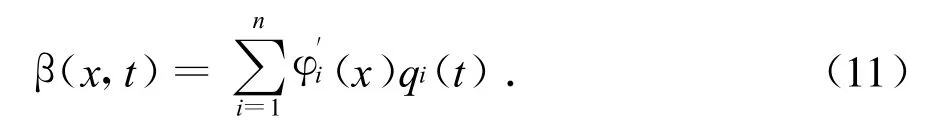
假定悬臂梁在加强层的转角为β时,存在可能的虚位移δ β,当β很小时,有sin β≈β.则由阻尼力产生的力偶做的虚功可以计算如下:

从而得到以下阻尼矩阵:

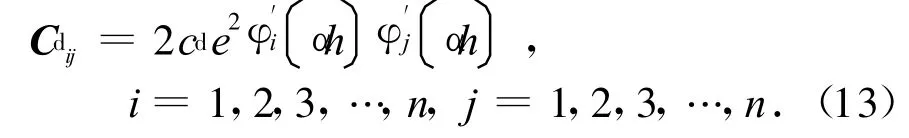
假定结构各阶固有模态阻尼均为ζ,则结构固有阻尼矩阵可以计算如下:

其中diag(◦)为对角矩阵;Φ为结构固有振型;ωi,mi分别为第i阶无阻尼固有频率与模态质量,最后结合式(13)～式(14)就可得到结构的总阻尼矩阵.

2.3 有限元模型

为验证基于假定振型法的模型,建立有限元模型与其对比.每个楼层简化为一个有限元节点,每个节点具有一个平动自由度和一个转动自由度.对于2维梁单元,其对应的单元刚度矩阵Ke和一致质量矩阵Me分别为:

其中:L为单元长度,据此可以组装得到结构的整体刚度矩阵与质量矩阵.由加强层阻尼系统产生的结构附加阻尼矩阵直接给出如下:

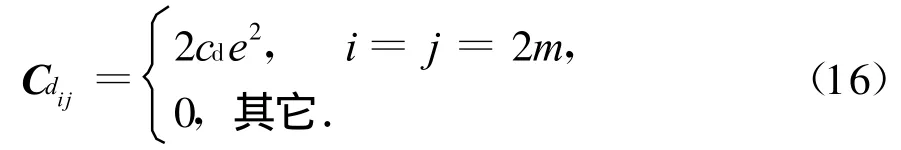
其中:m为加强层处有限元模型的单元节点号.同理,结构的固有阻尼矩阵Ci可以参照式(14)得到.

3 参数化分析

某高层框架-核心筒结构,高140 m,40层,外框架平面尺寸为30 m30 m.取一个方向进行研究,简化后的结构参数为ρ A=1.2×105kgm-1;EI=1.4×1013Nm2;h=140 m;e=15 m.参考Smith对传统加强层的位置优化研究[2]及文献[9]的加强层阻尼系统工程实例,加强层宜设计在结构中间左右高度处.再结合悬臂梁转角固有振型,见图2.当α=0.5时,二阶与四阶振型值φ′(α h)≈0;α=0.7时,三阶振型值φ′(α h)≈0,因此α=0.6被视为加强层的可能合理位置.与文献[9]的加强层阻尼系统工程实例类似,计划在该方向的4个加强墙与之临近的4个外围框架柱安装8个粘滞液体阻尼器,具体安装见图3[10],阻尼器的两端分别与框架柱和加强层的墙体铰接,加强层与框架柱之间的竖向位移差即为阻尼器的位移.

图2 悬臂梁无阻尼转角振型Fig.2 The first four angle mode shapes of a cantilever beam

图3 加强层阻尼系统安装示意图Fig.3 The layout of the outrigger damping system

进行复特征值求解,首先要得到系统的状态矩阵,对于假定振型得到的多自由度模型和有限元模型,系统状态矩阵可统一表示如下:

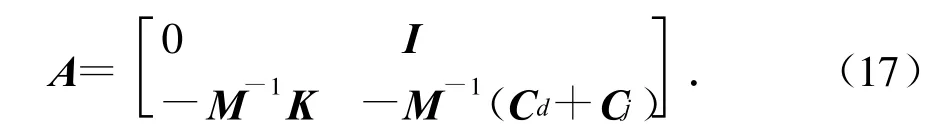
使用Matlab软件进行复特征值求解,通过对比发现,对于结构前四阶的优化阻尼常数求解,假定振型阶数n取8时,就可以得到与具有80个自由度的有限元模型相同的精度.在不同阻尼系数下,结构的振动频率与模态阻尼比见图4.从图4(a)可以看出,随着结构阻尼的增大,存在模态迁移现象,高阶振型逐渐向其最接近的低阶振型转化.正如文献[12]研究指出,当阻尼器位于支座附近时(如拉索振动控制系统[11]),结构的反共振频率(即阻尼器阻尼系数无穷大下的结构振动频率)与结构固有频率(即阻尼器的阻尼系数为0)比较接近时,在最优设计的阻尼器参数下,可以达到中等大小的模态阻尼比,不至于达到临界阻尼.相反,当阻尼器离支座较远时,由于结构的反共振频率与结构固有频率相差太大(如本文的加强层减振系统),结果将大大不同.从图4(b)还可以看出,低阶振型所需的最优阻尼系数较大,反之,高阶较小.

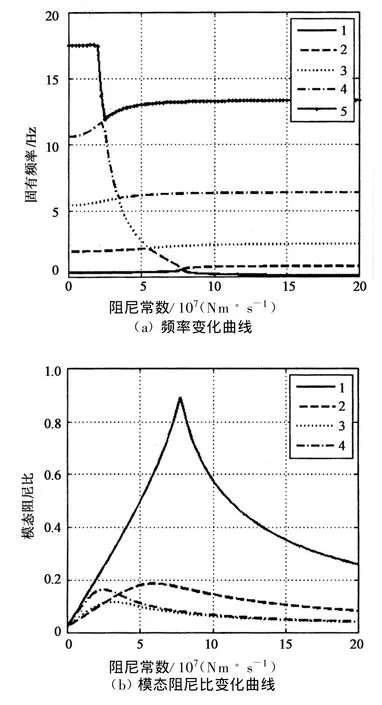
图4 结构振动频率、模态阻尼比随阻尼器阻尼系数变化曲线Fig.4 Structural frequencies and modal damping ratios versus the damping constants

4 减震效果仿真分析

在设计阻尼器前,首先要定一个目标阻尼比,按照我国抗震规范,结构附加阻尼比不宜超过20%.此外,一般认为,8%～10%的模态阻尼比即可消除由风荷载共振响应引起的结构反应放大[10].因此,为经济考虑,本文将目标阻尼比确定在10%左右.结合图4(a)可以看出,在cd＜2×107Nm/s时,结构前四阶振型尚未发生迁移,表明此时未达到临界阻尼,结构前四阶模态阻尼比分别为20.1%,9.3%,10.1%和15.6%.考虑到强震作用下,阻尼器的速度一般会达到0.2～0.3 m/s,此时对应的线性粘滞阻尼器的最大出力要达到6 000 kN.为降低阻尼器的尺寸与成本,阻尼系数选为1.2×107Nm/s,最大设计出力为3 000 kN.此时结构前四阶模态阻尼比分别为12.8%,9.3%,10.1%,15.6%.

基于Matlab-Simulink平台,对结构在400 gal的罕遇地震激励进行了仿真分析,地震波选用1940 EI Centro波.图5给出了结构各楼层的最大绝对位移与层间位移,图6给出了顶层的绝对位移与相对位移时程曲线,图7给出了基底剪力的时程曲线.从图5～图7可以看出,加强层阻尼系统非常有效,结构顶层位移、相对位移,基底剪力的极值相对无附加阻尼器的情况下,分别下降了52.9%,53.1%与13.1%.

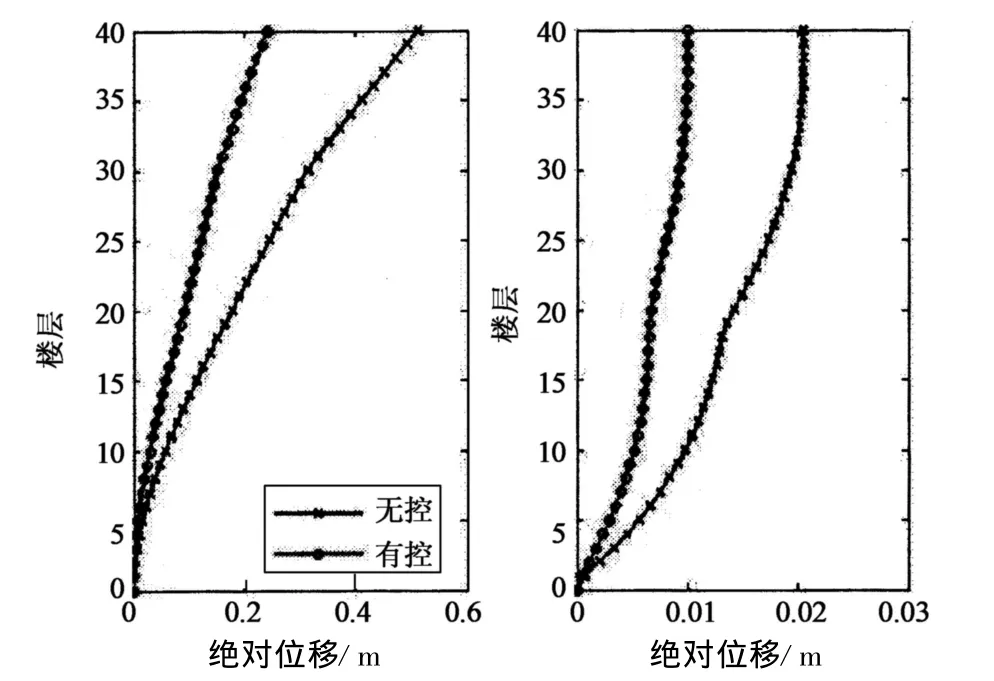
图5 位移响应包络线Fig.5 The envelopes of absolute and relative displacement

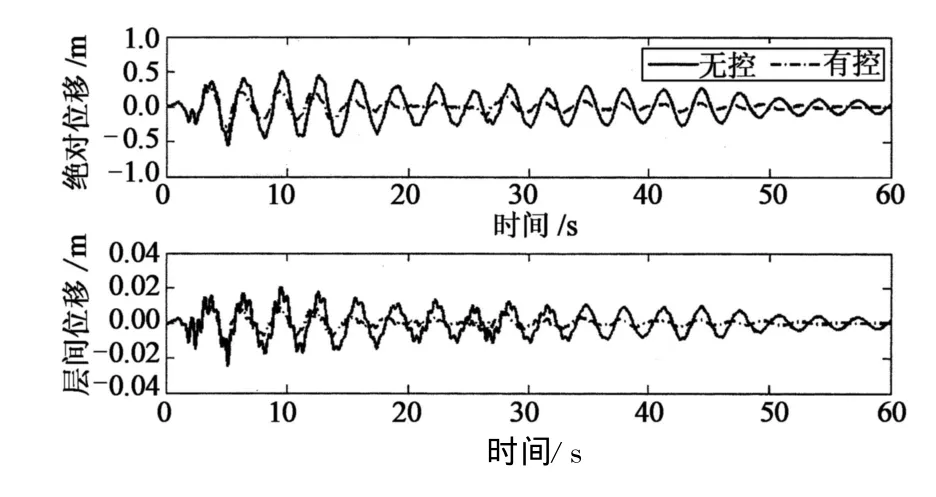
图6 顶层绝对位移与相对位移时程曲线Fig.6 The time histories of absolute and relative displacement of the top story

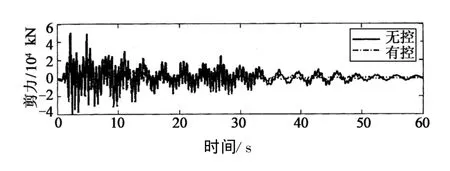
图7 结构基底剪力时程曲线Fig.7 The time history of structural base shear

图8进一步给出了阻尼器的耗能曲线,从图中可以看出阻尼器的位移达到近6 cm,相对普通的层间位移有较大的放大,从而取得了较好的减震效果.

图8 阻尼器耗能曲线Fig.8 Damping force versus damper displacement

5 结 语

将传统高层建筑的加强层与外围框架柱分开,并利用二者之间相对大的位移差,布设竖向粘滞阻尼器.该耗能减振系统通过牺牲加强层与外围框架柱协同工作时的附加静力刚度,而换取结构动力性能的改进.基于简化模型优化设计的最优阻尼器位置及阻尼系数可以为该类结构的初步设计提供重要参考,当然最终设计仍然需要采用非线性有限元的时程分析方法进行校核.虽然工程中更倾向于使用非线性粘滞阻尼器,但一般均可按线性粘滞阻尼器的初步设计决定阻尼器位置与阻尼系数,再调整非线性粘滞阻尼器的速度指数.为使该技术能够更好地应用于实际工程,下一步拟结合具体工程背景,开展工程应用研究,解决工程应用时的诸多实际问题.

[1] 聂建国,田淑明,矫金广.框架-核心筒组合结构体系在选型中的刚度规律[J].建筑科学与工程学报,2008,25(1):10-17.NIE Jian-guo,TIAN Shu-ming,JIAO Jin-guang.Stiffness regularity in option of frame-corewall composite structure systems[J].Journal of Architecture and Civil Engineering,2008,25(1):10-17.(In Chinese)

[2] SMITH B S,SALIM I.Parameter study of outrigger-braced tall building structures[J].Journal of Structural Division,ASCE,1981,6:2001-2014.

[3] 阮永辉,吕西林.带水平加强层的超高层结构的力学性能分析[J].结构工程师,2000,4:12-16.RUAN Yong-hui,LU Xi-lin.Structural analy sis of super high-rise structures with strengthed storey[J].Structural Engineers,2000,4:12-16.(In Chinese)

[4] 沈蒲生,陈宇.带加强层的高层框架-变截面核心筒结构的自由振动分析[J].建筑科学与工程学报,2007,24(3):19-24.SHEN Pu-sheng,CHEN Yu.Free vibration analy sis of tall frame and changed-section core wall structures with outrigger[J].Journal of Architecture and Civil Engineering,2007,24(3):19-24.(In Chinese)

[5] 黄怡,王元清,陈宏,等.水平加强层对超高层钢框架-支撑结构的影响[J].重庆建筑大学学报,2005,27(3):49-56.HUANG Yi,WANG Yuan-qing,CHEN Hong,et al.A study on the effect of horizontal strengthened story to super high-rise steel braced frame[J].Journal of Chongqing Jianzhu University,2005,27(3):49-56.(In Chinese)

[6] 沈蒲生.带加强层与错层高层结构设计与施工[M].北京:机械工业出版社,2009.SHEN Pu-sheng.Design and construction of high-rise buildings with outriggers and staggered floors[M].Beijing:China Machine Press,2009.(In Chinese)

[7] 周云,邓雪松,吴从晓.高层建筑耗能减振新体系概念与实现[J].工程抗震与加固改造,2007,29(6):1-9.ZHOU Yun,DENG Xue-song,WU Cong-xiao.The concept and realization of the new systems of tall building with dissipated devices[J].Earthquake Resistant Engineering and Retrofitting,2007,29(6):1-9.(In Chinese)

[8] JEREMIAH C.Application of damping in high-rise building[D].Boston:Massachusetts Institute of Technology,2006.

[9] SM ITH R J,WILLFORD M R.The damped outrigger concept for tall buildings[J].The Structural Design of Tall and Special Buildings,2007,16:501-517.

[10]WILLFO RD M,SMIT H R,SCOTT D,et al.Viscous dampers come of age[J].Structure Magazine,2008,6:15-18.

[11]JOHNSON E A,CHRISTENSON R E,SPENCER B F.Semi-active damping of cables with sag[J].Computer-Aided Civil and Infrastructure Engineering,2003,18:132-146.

[12]ENGELEN K,RAMON H,SAEYS W,et al.Positioning and tuning of viscous damper on flexible structure[J].Journal of Sound and Vibration,2007,304:845-862.