基于三维有限元方法的非晶合金变压器磁心电磁场分析

冯 超 杨向宇 龚 晟

（华南理工大学电力学院，广州 510641）

1 引言

非晶合金是一种新型的导磁材料，用非晶合金材料为磁心的配电变压器相比用硅钢片作为磁心的变压器空载损耗下降70%以上，空载电流下降约80%。随着非晶合金材料价格的逐步下降，现在已经是推广非晶合金合金变压器的好时机。因此，对非晶合金变压器电磁场进行全面分析，完善该种变压器的设计方法是非常有现实意义的。本文以三维有限元计算方法作为工具，对非晶合金变压器进行三维电磁场仿真和分析，考虑了拐角、边缘等因素对磁路的影响，并对比传统的磁路法计算设计变压器的方法，对其进行了修正和完善。

2 非晶合金变压器磁心结构和绕组联结组别

考虑非晶合金材料的特性，非晶合金变压器磁心的总体结构通常为三相四框式，如图1所示。图中变压器由4个单框卷磁心组合而成，有两个旁轭可供磁通中的高次谐波或零序分量流通框与框之间有较大的气隙，使磁通很难穿越。当变压器投运后,磁心柱中的奇次谐波能相互抵消，可降低漏抗压降，改善电流质量。

图1 非晶合金变压器磁心示意图

磁心截面为矩形，因此一、二次绕组均加工成带圆角矩形，从而提高了导线的利用率。与采用多级圆形截面磁心相比，可节省磁心及电磁线材料，并提高油箱内的填充率。

A、B、C三相绕组分别缠绕在中间的三个柱上。由于磁心采用三相四框式结构时，有两个旁轭可供磁通中的高次谐波或零序分量流通，因此，Yyn0联结法是不合适的，应采用Dyn11联结法。因为前者易造成绕组过电压，绝缘相对不安全，亦会使损耗增加，而后者则相反。

3 三维电磁场仿真原理概述

在配电变压器三维电磁场仿真中，由于频率较低，因此可以采用准稳态三维电磁场分析。下面对应用三维电磁场有限元分析的原理作简要介绍。

矢量磁位A满足下面方程

利用狄利克雷边界条件条件以及适用于对称面的齐次诺曼条件

磁导率μr有突变的界面上的连续性条件为

以及

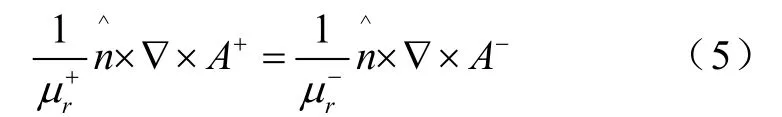
在任何有限元分析中，都需要将被分析的区域离散。在此，我们将体积V分成M个小体积单元，每个单元的形状为四点四面体，如图2所示。

图2 四点四面体积单元体

接着，用式（6）分析有n个节点的某个单元。再对所有单元进行组合，并强加驻点条件后，可得方程组

可以根据上面的方程组，解出每个结点上的磁势。经研究证明，上述三维有限元的相关方程对于求解磁密B和电流产生的能量，具有惟一性。

4 非晶合金变压器磁心与绕组的三维建模过程

4.1 非晶合金变压器磁心

建立磁心三维模型的时候，主要根据窗口高度、窗口宽度、叠厚和磁心宽度进行绘图，这四个量的具体意义如图3所示。

图3 磁心框示意图

绘图完成之后，把四个磁心模型的材料定义为非晶合金，这样，就完成了对磁心的三维建模。

4.2 非晶合金变压器绕组

绕组的材料是铜线。变压器的绕组包括高压侧三相绕组和低压侧三相绕组。

绘图的时候，对绕组进行理想的集中处理：假设在变压器原型中，在高、低压侧中，某侧某相的相电流为I，绕组匝数为N。在建模时用一个绕组代替N个绕组，因此在设定该绕组电流的时候，给这个绕组的电流设为IN，即直接输入总磁势F；这样，这个绕组产生的磁势效果就跟N个绕组产生的总磁势一样，并不妨碍对磁心磁密的分析。对于其它每侧每相的绕组，都如此处理。这种方法的好处是在以磁心为主要分析对象进行三维有限元计算时候，大大缩短了计算时间。

另外，为了给绕组定义电流，以形成磁势，需要知道实际变压器的绕组电流和绕组匝数。以Dyn11联结组别为基础，可以得到下列计算绕组电流和磁势的公式。

U1为高压侧相电压；U1N为高压侧额定电压。

U2为低压侧相电压；U2N为低压侧额定电压。

P为变压器额定功率；I1为高压侧额定相电流；I2为低压侧额定相电流。

为了计算绕组的匝数，先要确定每匝绕组的电压

B0为最大工作磁密，一般取1.25T～1.38T；A0为绕组包裹的磁心部分的横截面积，单位为cm2。

高压侧绕组匝数的计算公式为

低压侧绕组匝数的计算公式为

由绕组电流和绕组匝数，可以计算出原副边磁势1

F为高压侧每相磁势有效值；F2为低压侧每相磁势有效值。

在高压侧上，每相磁势的有效值为F1；另外，高压侧还必须产生一个励磁磁势，用以实现高压侧通过磁心给低压侧传递能量，把这个励磁磁势的有效值表示为F0，它与F1得变化规律相同。从而可知，高压侧产生的总磁势的有效值为（F1+ F0）。

表1列出了各相原副边绕组的总磁势。

表1 高、低压侧各相总磁势

5 三维电磁场仿真实例

以30kVA的非晶合金变压器为研究对象，高压10kV，低压0.4kV，设计时最大工作磁密取1.38T，联结组别为Dyn11。磁心的尺寸（A×B×C×D）为：

根据磁心尺寸对非晶合金变压器进行三维建模。在每相中，高压绕组在外，低压绕组在内。三维图如图4～5。

图4 非晶合金变压器磁心与绕组仿真模型

图5 非晶合金变压器磁心与绕组仿真模型

被绕组包围的磁心的横截面积A0=110cm2。取F0=5.716。根据式（8）～（16），可得F1=2965A，F2=2965A。

如表1所示，仿真时应该选取关键的时间点。由于磁势三相对称性，在图1中，对于左边第一个磁心和左边第二个磁心，只要能分别证明当它们的磁势达到最大时，它们依然不会处于饱和状态，那么就可以判断此非晶合金变压器就不会工作于饱和状态。经过对磁势的极值计算，可以知道，当ωt=0时，图1中左边第一个磁心的磁势达到最大值；当ωt=-π/6时，图1中左边第二个磁心达到最大值。因此，取这两个时间点进行分析计算。

由于三维有限元方法的计算量较大，综合考虑计算时间和计算精度，选择较为合适的网格剖分大小。对于磁心拐角处和绕组包围的磁心部分，采用较小网格剖分，提高计算精度；对于磁心的其余部分采用较大的网格剖分，减少计算时间。仿真结果如下：

当ωt＝0时，仿真结果见图6～8。

图6 当ωt＝0时磁心的剖分图

图7 当ωt＝0时的磁心磁密仿真图

图8 当ωt＝0时的磁心磁密仿真图

当ωt＝-π/6时，仿真结果见图9～10。

图9 当ωt＝-π/6时磁心的剖分图

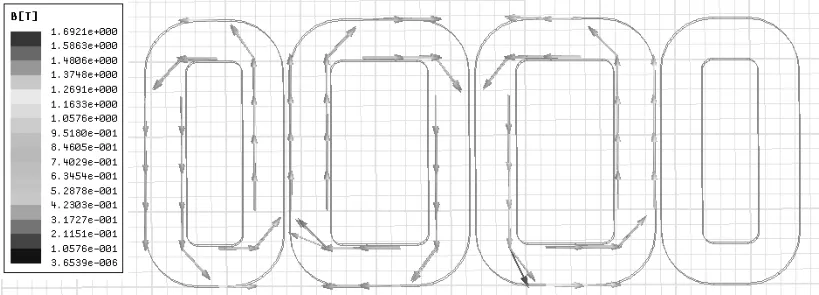
图10 当ωt＝-π/6时磁心磁密仿真图

图11 当ωt＝-π/6时磁心磁密仿真图

仿真结果显示，在这两个关键的时间点，除了磁心的某些拐角处，磁心的其他部位的磁密幅值都没有明显大于最大工作磁密1.38T，即没有处于饱和状态；在磁心的某些拐角处，磁密突然增大，超过最大工作磁密，但是，这也是变压器实际运行时的常见现象，并不会对整个变压器磁心正常运行有太大影响。下面用磁路计算设计方法与本文的三位电磁场有限元分析方法进行对比。

6 传统磁路计算方法

磁路法是一种计算磁路的经典方法，由于其简单直观，一直有着广泛的应用。因此，可以用磁路法计算非晶合金变压器磁心的磁密，通过对二者的比较，体现三维电磁场仿真的特点。

磁路法的形式与电路的欧姆定律相类似，其基本方程为

其中，r为磁阻，形式上类似电路中的电阻；φ为磁通，形式上类似电路中的电流；F为磁势，形式上类似电路中的电压。

磁阻r的定义为

其中，l为各段磁路长度；S为磁路的横截面积；μ为磁导率。

磁导率μ并不是一个恒定的值，它的表达式为

其中，B为磁密。它随着磁路上的磁场强度H的变化而变化；而磁场强度的表达式为

因此，磁导率μ是随着磁势F的变化而变化的。在用磁路法进行计算的时候，要根据磁势F的大小，在B-H曲线上选取相应的点，用公式μ=B/H求出实际的磁导率μ。

值得注意的是，在电路中，有一种计算方法叫做“网孔电流法”。在磁路法中，也可运用此方法的形式进行计算，只不过是在计算形式上中，用磁势F代替电压，用磁通φ代替电流，用磁阻r代替电阻。

根据四框五柱的结构，可以得出非晶合金变压器磁心的等效磁路，如图12所示。

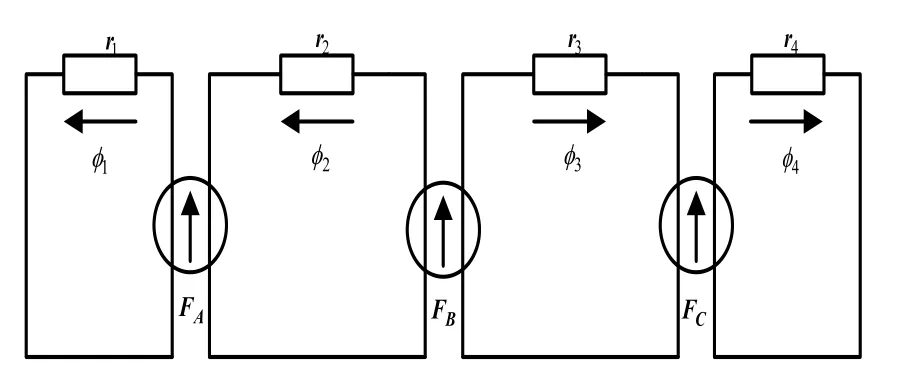
图12 非晶合金变压器磁心的磁路模型

利用磁路法基本方程可得方程组

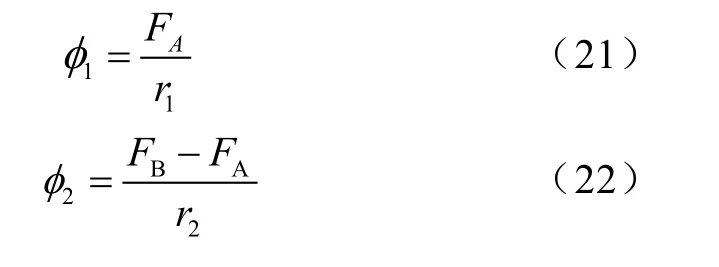
选取前述的两个关键时间点，根据式（19）～（24），结合三维建模过程中的一些数据，可以得到磁心磁密的计算结果：

磁路法计算结果与三维电磁场仿真结果相近，但其线性化的理想简化磁性材料使得计算的精度有所降低，有理由相信本文中的三位电磁场有限元分析方法获得的计算结果更为准确，对非晶合金变压器的设计的准确性提供了保障。

7 结论

本文利用三维有限元方法，应用四点四面对非晶合金变压器磁心进行剖分，然后通过矢量磁位-标量电位法对电磁场进行了计算仿真分析，获得了电磁场分布图。并通过与磁路法计算的对比，说明了三维电磁场仿真结果的有效性。得到了比磁路法更为精确的非晶合金变压器设计方法。

[1] 尹克宁.变压器设计原理[M].北京:中国电力出版社, 2003.

[2] 汤蕴璆 史乃. 电机学[M].北京:机械工业出版社, 2003.

[3] 金建铭. 电磁场有限元方法[M]. 西安: 西安电子科技大学出版社, 1998.

[4] 杨中地,武颖.非晶合金变压器[J].变压器,2007, 44(7): 1-8.

[5] 姜建华. 三相四框式磁心的磁路分析[J].变压器, 1998,35(6):7-10.