Cesaro-orlicz序列空间中的MLCU

麻振华 李鸿强

河北建筑工程学院数理系

1 引 言

本文中,R、R+、N分别表示实数集、非负实数集和自然数集.用 l0表示所有的实序列 x=(x.

定义1 我们称映射φ:R→[0,+∞)为Orlicz函数,如果:

(a)φ是凸的,且在R+中左连续;

(b)φ(u0)＞0 (u0≠0),且φ(0)=0;

(c)φ(u)→∞ (u→∞)[2].

定义2 对任何的Orlicz函数φ,我们在l0中定义凸模

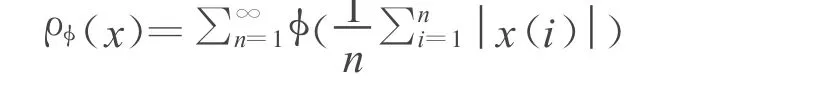
则我们称空间

为Cesaro-Orlicz序列空间.

我们在此空间中定义Luxemburg范数如下:

定义3 对任何的Orlicz函数φ,称φ满足Δ2条件(φ∈Δ2(0))是指存在K＞0和a＞0,满足φ(a)＞0,且对∀u∈[0,a]有φ(2u)≤Kφ(u).

定义4 设B(X)、S(X)分别为X中的闭单位球和单位球面.称点x∈S(X)为B(X)中的端点,如果对任意的y、z∈B(X)等式2x=y+z蕴涵着y=z.我们用E xt B(X)表示B(X)中的所有的端点.称Banach空间X为凸的(R),如果Ext B(X).

定义5 对任何的Orlicz函数φ,我们称[a,b]为φ的仿射区间(S AI),如果对∀ε＞0,φ在[a,b]上仿射,而在[[a-ε,b]或[a,b+ε]上则不然.我们用{[ai,bi]}i表示φ的所有仿射区间,显然有i

同时我们容易知道,对于∀u∈[a,b],存在A,B＞0使得φ(u)=Au+b.[2]

定义6 称Banach空间为局部中点一致凸(MLUC)的,如果对∀x∈S(X),和xn,yn∈B(X),xn+ yn→2x蕴涵着xn-yn→0[1].

2 结 果

引理1 若φ∈Δ2(0),则对∀x∈cesφ,

引理3 若φ∈Δ2(0),则cesφ是凸的⇔φ在[0,α]上严格凸.

其中,f(α)=1且f为如下函数:

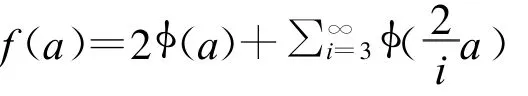
定理 若φ∈Δ2(0),则cesφ是MLUC⇔cesφ凸

证明:“⇒”由引理3可知,只需证明φ在[0,α]上严格凸即可.其中,f(α)=1且f为如下函数:f (a)=2φ(a)+.

假设φ在[0,α]上不严格凸,则存在[bn,c]⊂(0,α),使得φ在此区间中为仿射的,即对∀u0∈[bn, c],存在A,B＞0使得=Au0+B.其中bn＜b且bn→b.

因为c＜α,则有

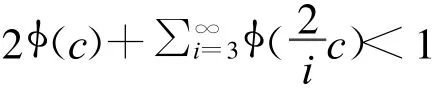
我们取d＞0,使得

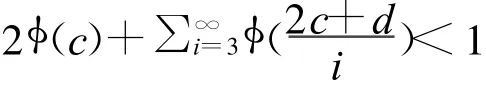
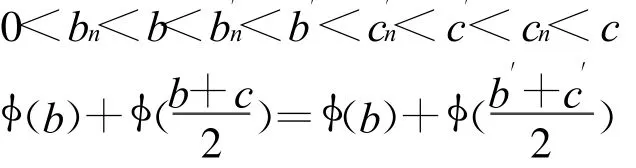
和

不失一般性,我们可设b+c+k=b′+c′,因此

取m＞0使得,

因为b+c+k=b′+c′可以得到

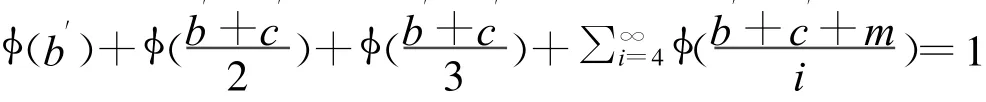
分别令

其中kn→k mn→m

则有xn→x′,yn→y′

其中

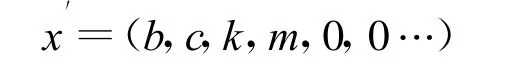
由于ρφ(x′)=ρφ(y′)=1

再由引理1可知

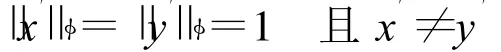
则

则x∈S(cesφ).

由于

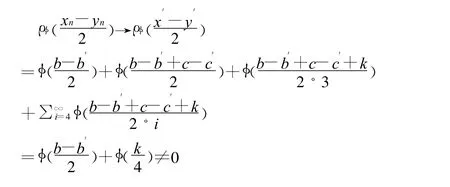
所以,xn-yn→/0

矛盾.

“⇐”对任何的x、xn、yn∈S(X),满足xn+yn→2,往证xnk-ynk→0.由于φ∈Δ2(0)时cesφ是可分的,则由于可分对偶空间是w*序列紧的,则{xn}和{yn}有子序列{xnk}和{ynk}为Eφ-w收敛于x′、y′∈S(cesφ),则xnk+ynk→x′+y′(依坐标收敛).

证毕.

[1]Cui yun-an and Hudzik H,Basic toplogical properties of Cesaro-Orlicz spaces,Proc.Indian Acad.2005,115,4.461～476

[2]陈述涛,Geometry of Orlicz spaces,Dissertiones Math.(The Institute of Mathematics,Polash Academy of Science)1996

[3]张剑宇,麻振华,崔云安,Cesaro-Orlicz序列空间的对偶空间.哈尔滨理工大学学报,2007,12(6):60～62