用于MIMO-OFDM系统盲信道估计的斜投影子空间法*

孙季丰 张志勇

(华南理工大学电子与信息学院,广东广州 510640)

为适应无线通信中多媒体应用对高速率数据传输的需要,正交频分复用(OFDM)与多输入多输出(MIMO)作为未来第四代移动通信中两种主要的技术被广泛关注.MIMO技术与OFDM技术的结合能够将空间分集、频率分集以及时间分集有机地结合在一起,可以大大提高无线通信中的信道容量和传输速率,并能有效地抵抗衰落、干扰和噪声.在实际应用中,为进一步提高系统的频谱效率,MIMOOFDM系统通常采用幅度非恒定的调制方式,接收端需要信道状态信息(CSI)才能进行相干解调,此外,空时编码的译码也需要有精确的CSI才能完成.因此,信道估计是MIMO-OFDM系统接收机设计的一项主要任务.

目前,对MIMO-OFDM系统中的信道估计方法的研究主要分为两大类:一类是基于导频或训练序列的非盲信道估计,它需要在发送端发送大量训练序列,浪费了部分频带资源,无法满足高速数据通信的需要;另一类是基于极少量导频或训练序列的盲信道估计,它主要利用接收信号的二阶统计特性[1-2],其中基于信号、噪声子空间分解的估计方法具有较好的估计性能,但是存在计算复杂度高、收敛不快、鲁棒性不好等缺点.

斜投影子空间法在信道估计及盲信号分离等方面有着广泛的应用.例如,将斜投影子空间法应用于单输入多输出(SIMO)系统的信道和符号联合盲估计中,能有效地抗加性有色噪声干扰[3-5];将斜投影子空间法应用在卷积信道的盲信号分离上,使得算法的复杂度有所降低[6];利用斜投影子空间法对混有有色噪声的系统进行子空间跟踪[7];利用最小二乘支持向量机及斜投影子空间法来对Hammerstein信道进行盲估计[8]等.本研究在以上文献基础上将斜投影子空间法应用于MIMO-OFDM盲信道估计中,不仅是对斜投影子空间法应用的推广,也为MIMO-OFDM系统盲信道估计提供了一个新的思路[9].

1 MIMO-OFDM系统模型

考虑单用户MIMO-OFDM系统,发送端配置有M根发射天线,接收端配置有 N根接收天线,假设OFDM子载波数为K,循环前缀数为P.

在发送端,数据源经过信源和信道编码后形成基带复信号,然后经过空时编码变成了 M列并行传输子信号流,最后通过OFDM调制后变成了M列并行时域信号流并独立在各个天线上发送.定义在发送端M根天线上发送的第n个信息符号块d(n)及其第k时刻数据源的频率d(n,k)分别为:

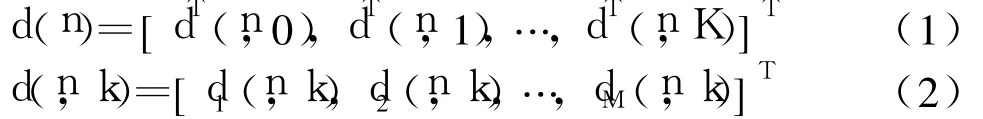
经过OFDM调制及添加循环前缀后,发送端M根天线上发送的第n个OFDM信息符号块s(n)及其第k时刻数据源的频率s(n,k)分别为:

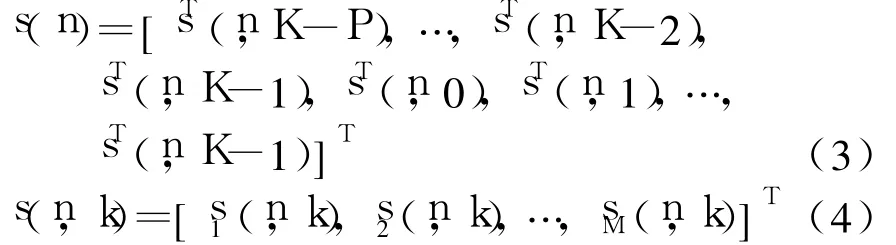
通常快速傅里叶逆变换(IFFT)矩阵可以表示为

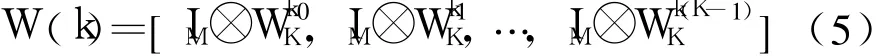
式中:IM为M×M的单位矩阵;为第k时刻的第ω(0≤ω≤k-1)个快速傅里叶反变换算子,即;⊗表示Kronecker积.根据公式(5)定义矩阵W′:

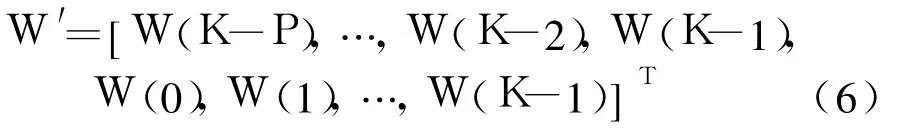
则信源d和s之间的关系可以表示为

将M根发射天线和N根接收天线之间的慢时变频率选择性信道等效为一个有限冲激响应滤波器(FIR),假设信道的多径条数最高为L+1,hL表示第L+1条多径信道的信道真实矩阵,那么据此可以定义一个(K+P)N×(K+P+L)M维的信道矩阵[10]:

同时也定义整个接收端N根天线上接收的第 n个OFDM信息符号块y(n)及其第k时刻时的数据源向量y(n,k)分别为:

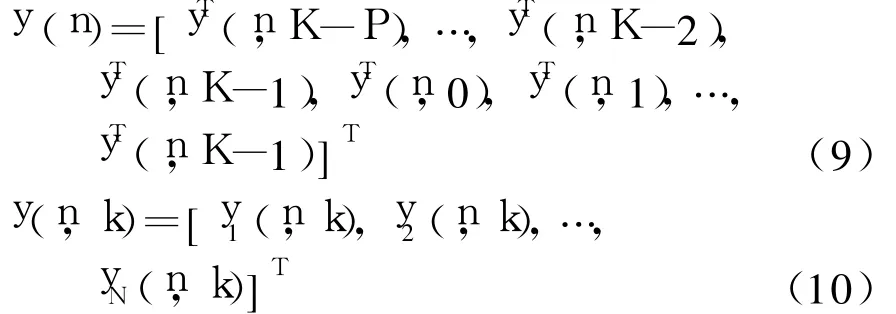
如果用式(1)来表示式(9),则有

式中:η(n)表示(K+P)N维的空间和时间均不相关的加性复高斯白噪声列向量,其均值为 O,方差为

2 斜投影信道估计算法实现

斜投影子空间法的基本原理为:若存在一个m′×n′维列满秩复矩阵 A,m′×t维列满秩复矩阵B,并且有(n′+t)＜m′,定义沿着B向A投影的斜投影算子为EAB,它的值空间为 {A},零空间为{B},{◦}表示矩阵列所张成的线性子空间,那么它有如下性质:

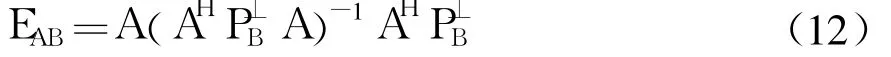
式中:(◦)H表示矩阵的共轭转置;PB是 {B}的正交投影算子,PB=B(BHB)-1BH,是 {B}的正交补空间的正交投影算子,,而且还可以证明

习惯上称 {A}为斜投影算子EAB的投影空间,

{B}为斜投影算子EAB的投影方向空间.斜投影算子作为正交投影算子的扩展,不要求子空间 {A}和 {B}相互正交,这样就使得斜投影算子的应用范围更广.

对接收和发送数据块分别做如下定义:

式中:a、b表示信号发送时刻,若a-L＜0,则s(n,a-L)=0;j表示矩阵Ya|b和Sa|b的行维数.在不考虑噪声的情况下,可以重写式(11),则有

式中:i=b-a+1;Hi与式(8)所定义的H有相似的结构,只是Hi的维数变为iN×(i+L)M.

实际上对MIMO-OFDM系统进行斜投影子空间盲信道估计利用的是式(16)所定义的信道模型.一般情况下,作如下假设:

(1)存在一个数据长度i0使得具有Toeplitz结构的信道传输矩阵 Hi0满足列满秩,即要求发射天线数M小于接收天线数N.

(2)系统发送信号Sa|a+i-1的线性复杂度必须大于2(L+i),即要求

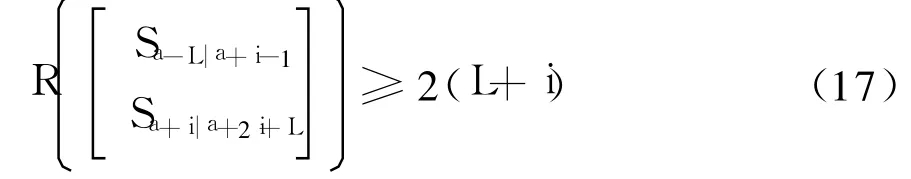
式中:R(◦)表示矩阵的秩;上面两个假设在斜投影估计中具有至关重要的作用,它们可以保证输入信号行向量所张成的子空间和输出行向量所张成的子空间是同构的,即对于满足条件的i＞i0,则有

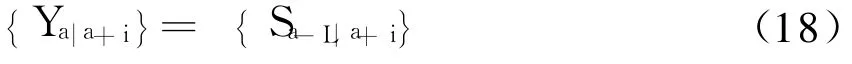
按照文献[5]的方式,将式(16)中接收数据块Y1|L+2i划分成“过去”、“现在”、“将来”3个子空间Ypa、Ypr、Yfu,其中,Ypa=Y1|i,Ypr=Yi+1|i+L,Yfu= Yi+L+1|2i+L.由式(18)的性质可以得出

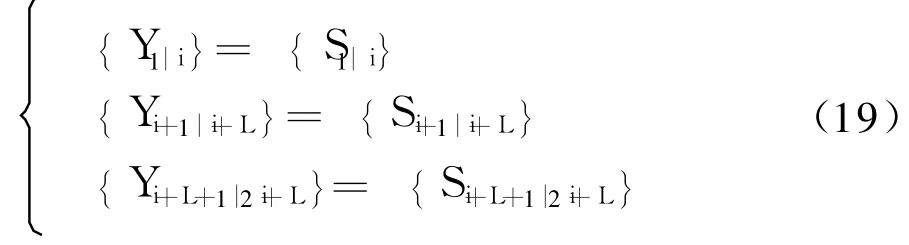
对于包含有完整信道状态信息的子空间{Ypr}而言,子空间 {Ypa}和 {Yfu}就是干扰,因此本研究的目的就是从 {Ypr}中除去 {Yfu}和{Ypa},对Ypr进行如下斜投影运算:

式中:EYpaYfu表示以 {Ypa}为值空间、{Yfu}为零空间的斜投影算子;E1表示把 Ypr沿着Yfu的方向向Ypa投影,E2表示把Ypr沿着Ypa的方向向Yfu投影,通过相应的变形可以得到E1和 E2的另一种表达式:

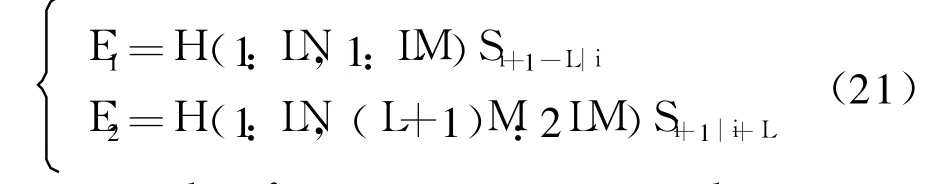
式中:H(c:d,e:f)表示取矩阵的第c到d行,第e到f列的矩阵块.那么:从式(21)中可以观察到E1和E2均没有包含完整的CSI,因此要通过E1和E2来构造新的矩阵使之包含有需要的信道矩阵[hL,hL-1,…,h0]T,定义矩阵Γ、Ω和ψ及相应的运算:

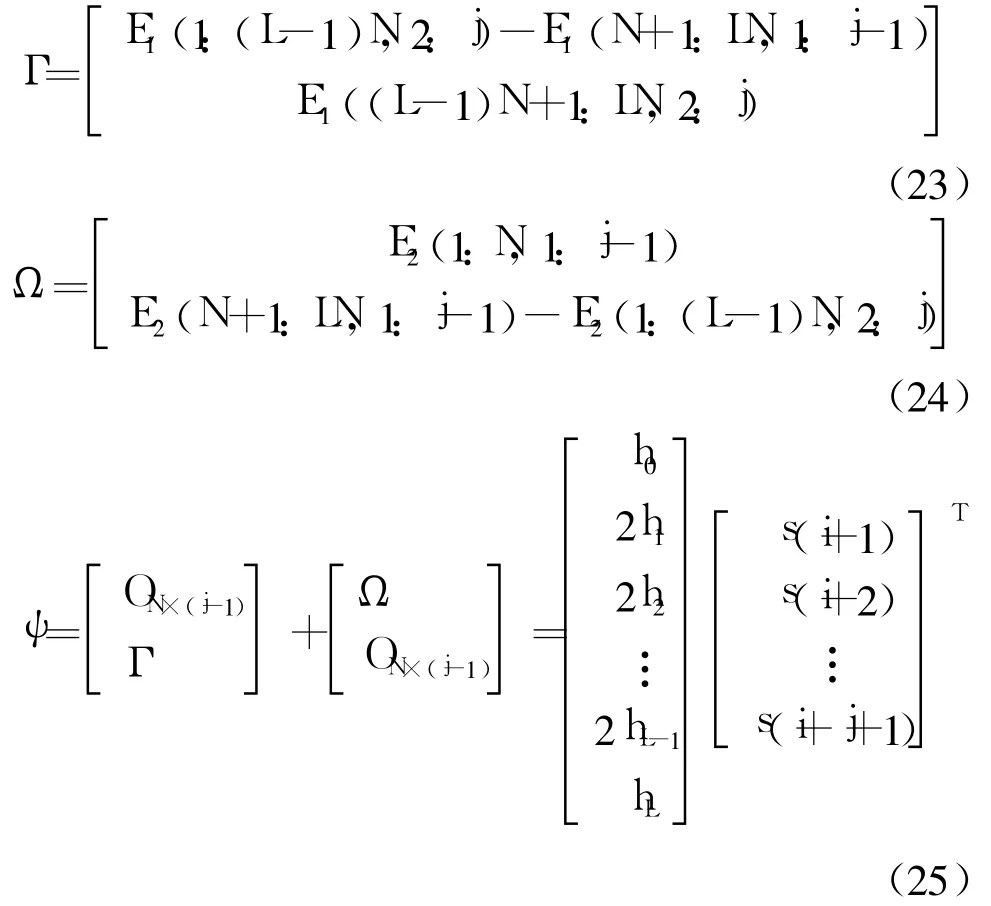
式中:ON×(j-1)表示N×(j-1)维的零矩阵.此外从式(25)可以看出,ψ包含了所有信道矩阵参数.当信道模型中不含有加性白噪声时,ψ的秩为 N,而当ψ混有加性白噪声时它的秩不再是N,此时对ψ进行奇异值分解(SVD)有

式中:θ为矩阵ψ的奇异值矩阵;V为ψ的右特征矩阵,是一个酉矩阵;U为ψ的左特征矩阵,是一个酉矩阵.那么所需要的信道状态矩阵为ψ的前M个最大奇异值所对应的左特征矩阵为

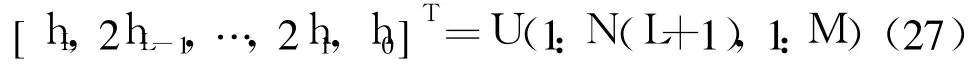
通过奇异值分解,最后得到的信道估计值与真实值会相差一个模糊矩阵b,b是M×M的非奇异矩阵.为估计模糊矩阵,需要在OFDM符号中加入极少量的训练序列,设信道状态矩阵真实值H′=[hL,…,h1,h0]T,估计值为H0,则

假设发送端M根天线上发送的第n个OFDM信息符号块第 时刻发送的训练序列为u(n,),相应的接收信号为x(n,),那么通过估计信道矩阵H0恢复出的发送序列 α为

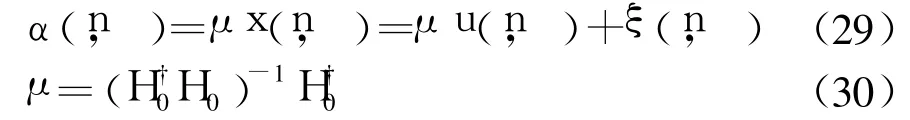
下面作如下定义:

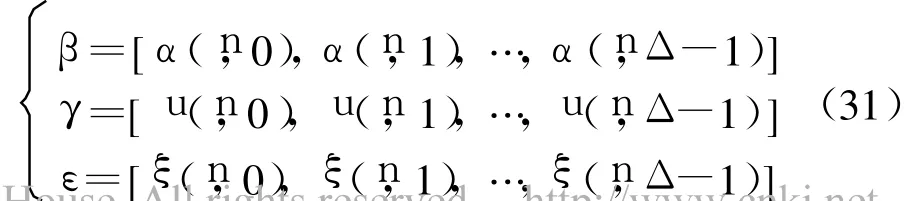
式中:Δ为发送训练序列码字的长度(Δ≥L+1); ξ(n,)为接收信号所叠加的白噪声表示估计信道矩阵的广义逆.此外,β、γ和 ε之间的关系可以表示为

通过下式可以估计出

3 仿真结果及分析

仿真实验中对算法的性能估计采用标准均方根误差(NRMSE)作为评价标准,其数学表达式为

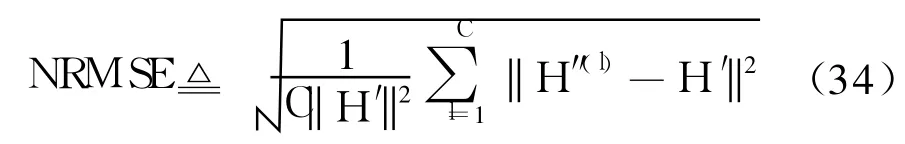
式中:C为蒙特卡罗仿真次数;H″(l)为第l次仿真的估计矩阵.在接收端定义信号的信噪比为

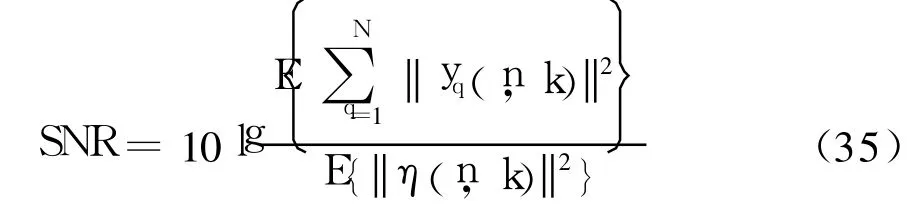
式中:E{◦}为随机信号的数学期望;yq[n,k]为第n个OFDM符号第k时刻第q根接收天线上的信号;η(n,k)为η(n)的一个元素.

实验仿真参数如下:信源调制方式为正交相移键控,信道编码采用码率卷积编码,空时编码采用 2×2的空时分组码,发射天线数为 2,接收天线数为3,OFDM子载波数为64,循环前缀数为12, MIMO信道采用3GPP TR信道,其中信道多径条数为6,中心载频为2GHz,移动台速度为10m/s,多普勒频移为65Hz,蒙特卡罗仿真次数为100.

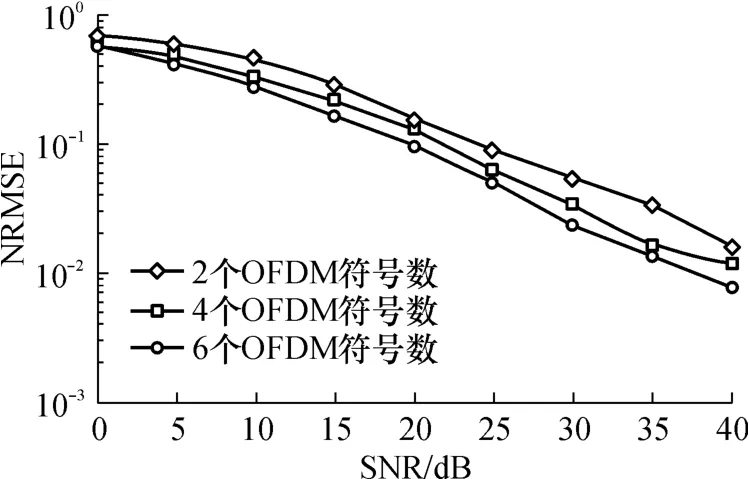
图1 不同信噪比下斜投影子空间法的估计性能Fig.1 Estimation performance of ob lique-p rojection subspace approach with different SNR

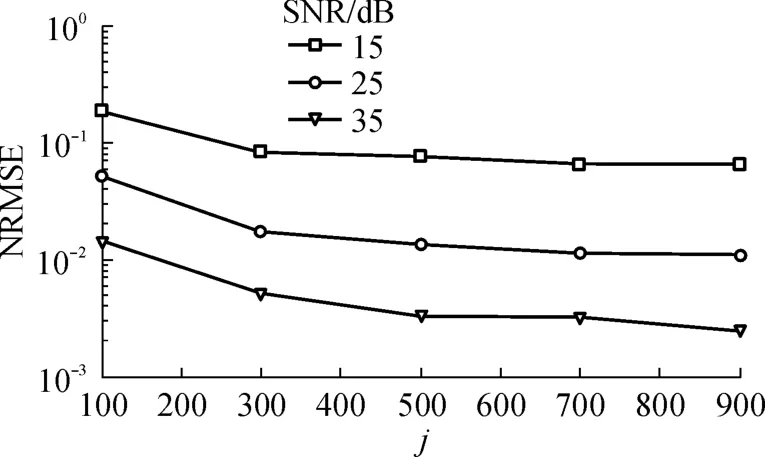
图2 参数j对斜投影子空间法估计性能影响Fig.2 Impact of parameter j on estimation performance of oblique-projection subspace approach

图1示出了在参数j分别为2、4、6个OFDM符号数时,信噪比的变化对斜投影子空间法估计性能的影响.由图 1可以看到,当信噪比低于 10dB时,估计性能变化不太大,说明文中算法比较适合应用于大信噪比下的信道估计.图 2示出了在不同信噪比下参数 j对斜投影子空间法估计性能的影响.由图2可以看到,算法估计性能是随着参数 j的增加变得更好,但是当 j增加到 500后,性能变化不是很明显.图3示出了斜投影子空间法与噪声子空间法的估计性能比较,从仿真结果可以看出,在相同参数j下(j为6个OFDM符号数),斜投影子空间法估计性能略低于噪声子空间法.

斜投影子空间法的计算复杂度主要来自于 LQ分解,即斜投影算子的计算,而噪声子空间法的复杂度主要来源于SVD,即接收信号相关矩阵的奇异值分解.经分析可知,斜投影子空间法的复杂度可以表示为O(j2),而噪声子空间法的复杂度为O(j3),结合仿真结果图 3可知,文中算法在牺牲少量估计精度的情况下可以大大降低计算复杂度,体现了文中提出的算法的有效性.

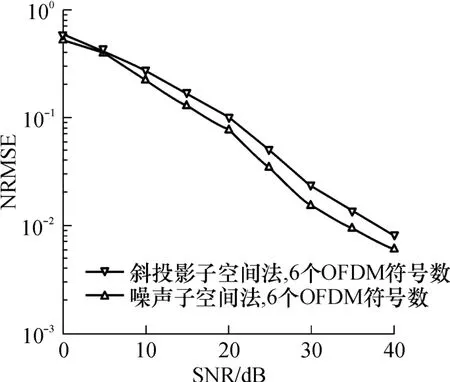
图3 斜投影子空间法与噪声子空间法的估计性能比较Fig.3 Comparison of estimation performance between obliquep rojection subspace approach and noise subspace app roach

4 结语

文中提出一种基于斜投影子空间法的MIMOOFDM盲信道估计算法.通过与噪声子空间算法的比较发现,文中提出的算法在牺牲少量估计精度的情况下可以大大降低计算复杂度,由于采用了奇异值分解法,文中提出的算法对于加性高斯白噪声具有一定的鲁棒性.本算法存在的不足是只能批量处理数据,因此,如何使用斜投影子空间法自适应跟踪信道是今后的研究课题.

[1] Zeng Yonghong,NgA Tung-sang.Sem i-b lind channelestimation method formultiusermulti-antenna OFDM systems [J].IEEE Transactions on Signal Processing,2004,52 (5):1419-1429.

[2] Tu Chao-cheng,Benoit C.Subspace blind MIMO-OFDM channel estimation with short averaging periods:performance analysis[C]∥W ireless Communications and Networking Conference.Las Vegas:IEEE,2008:24-29.

[3] Richard T B,Louis L S.Signal processing app lications of oblique projection operators[J].IEEE Transactions on Signal Processing,1994,42(6):1413-1424.

[4] Yu Xiang,Tong Lang.Joint channel and symbol estimation by oblique projections[J].IEEE Transactions on Signal Processing,2001,49(12):3074-3083.

[5] Piet V,Marc M.Two determ inistic blind channel estimation algorithms based on oblique projections[J].Signal Processing,2000,80(3):481-495.

[6] Peng Chunyi,Zhang Xianda,CaiQutang.A block-adaptive subspacemethod using oblique projection for blind separation of convolutivem ixtures[C]∥Advances in Neural Networks 2005.Berlin-Heidelberg:Springer-Verlag,2005: 526-531.

[7] Chen Minhua,Wang Zuoying.Subspace tracking in colored noise based on oblique p rojection[C]∥Acoustics, Speech and Signal Processing.Toulouse:IEEE,2006:Ⅲ556-Ⅲ559.

[8] Ivan G,Kristiaan P,Johan A K.Subspace identification of hammerstein systems using least squares support vector machines[J].IEEE Transactions on Automaic Control, 2005,50(10):1509-1519.

[9] 张玲,张贤达.MIMO-OFDM系统的盲信道估计算法综述[J].电子学报,2007,35(6A):1-6.

Zhang Ling,Zhang Xian-da.An overview of blind estimation algorithm for MIMO-OFDM systems[J].Acta Electronica Sinica,2007,35(6A):1-6.

[10] 侯伟昆,叶梧,冯穗力,等.快变信道下OFDM系统的判决反馈信道估计[J].华南理工大学学报:自然科学版,2008,36(8):48-53.

Hou Wei-kun,Ye Wu,Feng Sui-li,et al.Decision feedback channel estimation of OFDM systems in fast timevarying channel[J].Journal of South China University of Technology:Natural Science Edition,2008,36(8): 48-53.