非均匀采样系统时基失真的一种新评价方法
梁志国 孟晓风
(北京航空航天大学 仪器科学与光电工程学院,北京 100191)
非均匀采样系统时基失真的一种新评价方法
梁志国 孟晓风
(北京航空航天大学 仪器科学与光电工程学院,北京 100191)
提出了在多 A/D合成采样系统这种非均匀采样系统中,使用时基微分非线性和时基积分非线性概念评价采样时基失真的新方法.使用正弦波激励系统,将各个子 A/D的数据分别抽取形成子抽样序列,用最小二乘正弦波曲线拟合法,获得各个子抽样序列初始相位差,该相位差对应的时间差,即是各个子 A/D间的采样延迟时间,它们的一致性,即是系统的采样均匀性,体现了时基失真特性,用时基微分非线性和时基积分非线性描述.在一组仿真数据上进行的实验验证了方法的正确性.在数字存储示波器的实测数据上进行的实验验证了方法的可行性.方法可以用来评价非均匀采样系统的采样时基失真.
时基;失真;非均匀采样;曲线拟合;校准;评价
非均匀采样技术,通常指通过多个低采样速率的 A/D组合起来,实现一个等效高采样速率A/D功能和效果的技术,属于现代高速数字存储示波器、瞬态波形记录仪等高速采样仪器系统中的基本技术之一.其直接效果是以较低速的硬件技术可以实现较高速的采样效果,而带来的负面影响,则是所实现的等效高速采样序列不可能是理想的等间隔均匀采样序列,由此引出了非均匀采样理论和技术,以及其相应的评价校准问题.有关采样不均匀及其影响评价的研究已有很多[1-18],近年来仍在持续取得进展.
文献[5-6]研究了数据采集系统中的帧抖动问题,指出它与取样示波器中抖动的不同点是它属于序列抖动,而不是序列中每一个采样点时刻的随机抖动,并讨论了其影响和通过硬件的抖动识别方法.
文献[7]研究了叠加高斯噪声的采样孔径抖动测量,在孔径特性与信号频率选择无关的采样通道中,证明了孔径抖动可影响输入信号采样波形,与叠加的高斯噪声互相独立.此前认为叠加噪声功率与孔径抖动噪声功率成正比.
文献[15]针对实时测量系统的时基失真,结合使用拍频、最大似然估计等方法,将时基失真与其它噪声等有效分离,从而最终达到测量并滤出时基失真的目的.
文献[16]研究了用于非均匀采样但拥有确定时间标签的测量序列的两种滤波方法:①差分方程时间修正法;②类 FIR滤波器法.文献[17-18]研究了抖动存在时重构测量序列问题.
与前人研究的侧重点不同,本文试图借用采样量化系统中评价 A/D线性度指标的微分非线性和积分非线性概念,评价非均匀采样系统中由于多个子 A/D的合成采样带来的时基失真,称其为时基微分非线性和时基积分非线性.
1 测量原理和方法
图1所示为用 M个子 A/D构造一个等效高速 A/D的非均匀采样系统,对于每个子 A/D——ADCk来说,属于等间隔采样子系统,采样速率均为 v/M,相邻子 A/D的延迟时间差 τk理想值为系统采样间隔 τ=1/v.
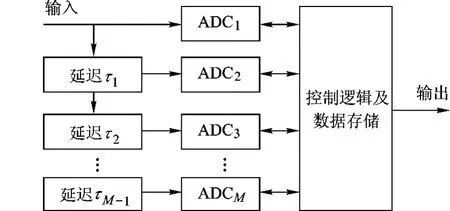
图1 多A/D组成的单A/D非均匀采样系统
实际上,输入信号通过本级子 A/D——ADCk后,经时间延迟 τk,进入下一个子 A/D——ADCk+1,由此实现了以M个采样速率为v/M的子A/D,获得采样速率为v的合成 A/D的采样效果,从而实现了非均匀采样系统的高速采样过程.
时基失真测量的基本思想,是在已知非均匀采样系统子 A/D数目 M的前提下,从系统对于正弦波的测量序列中,经过二次抽样获取各个子A/D自己的采样子序列,从相邻子序列间的相位差对应的延迟时间差中,获得非均匀采样系统的时基微分非线性和时基积分非线性.过程如下.
如图 1所示,设非均匀采样系统由 ADC1,ADC2,…,ADCM等 M个子 A/D合成构成一个高速 A/D,系统采样间隔 τ,采样速率 v,则各个相邻子 A/D的理想延迟时间为 τk=τ,k=1,2,…,M-1,子 A/D理想采样速率为 v/M.给系统加载低失真正弦波激励 e(t):
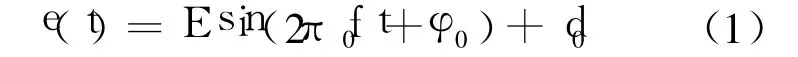
式中,E为正弦波幅度;f0为正弦激励信号频率;φ0为初始相位;d0为信号的直流偏置.
获得采集数据序列{xi,i=1,2,…,n}.以子A/D个数 M为间隔对序列{xi}进行二次抽样,从采样序列{xi,i=1,2,…,n}中抽取 M个子序列
子序列{yk(m),m=1,2,…,n/M}对应 ADCk子 A/D的采集数据,k=1,2,…,M.
按最小二乘法求子序列{yk(m)}的拟合信号[8]:
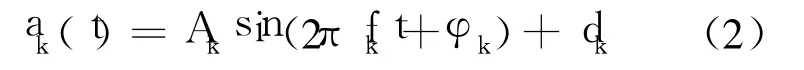
采集数据序列{xi}的第 i个测量点 xi对应的时刻 ti=i/v,i=1,2,…,n;二次抽样后形成的子序列{yk(m)}的第 m个测量点 yk(m)对应的时刻tm=tk+(m-1)τ,m=1,2,…,n/M;则式 (2)可写为

记为

拟合残差有效值 ρk:

当 ρk=min时,可得 ADCk的采集子序列{yk(m)}的最小二乘拟合正弦参数 Ak,ωk,φk和 dk,则 ADCk+1对于 ADCk的采样时间延迟 τk:
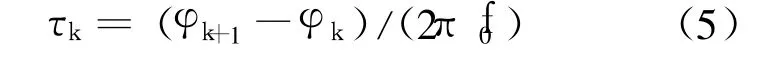
设各个延迟时间 τk的平均值为 τ,则第 k个子 A/D的时基微分非线性:
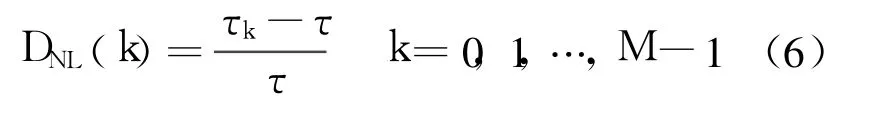
全系统的时基微分非线性:
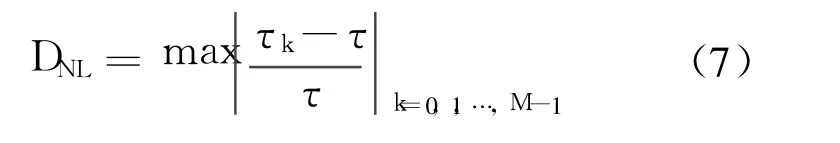
第 k个子 A/D的时基积分非线性:
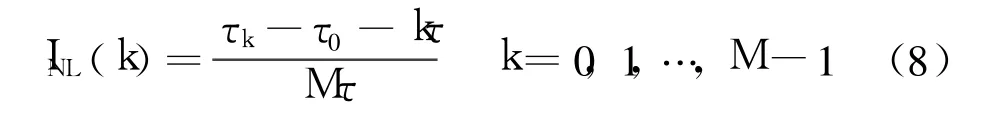
全系统的时基积分非线性:
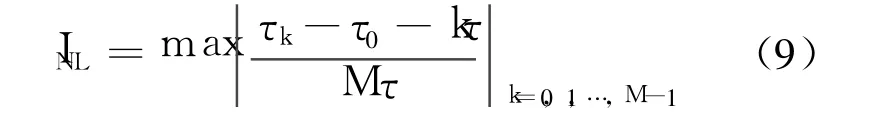
τk的测量不确定度可参见文献[19-20]进行评定,若想获得更精确的延迟测量结果,也可针对各个子 A/D的子序列使用数字滤波方法进行预处理后再进行相应计算[21].各个延迟时间 τk的平均值为 τ的不确定度可以由 τk的不确定度平均次数 M简单获得,积分非线性和微分非线性的不确定度评定已经获得解决,此处不再赘述.
2 仿真实验结果
设定非均匀采样系统的测量范围 ±5V,τ=250ps,v=4GSa/s,A/D位数为 24 bits,采样点数n=15000.设定子 A/D数 M=16,其理想延迟时间为 τb=τ=250ps,仿真延迟时间值 τkb如表 1所示设定 .Δτkb=τkb-τb.
选取 f0=6254321Hz,E=4V.经过仿真非均匀采样,可获得其曲线波形如图 2所示,从其中的抖动可明显看出非均匀采样时基失真的影响.使用失真度分析手段[22],可以得到其总失真度为4.26%.这应该主要是由于非均匀采样带来的测量波形失真.
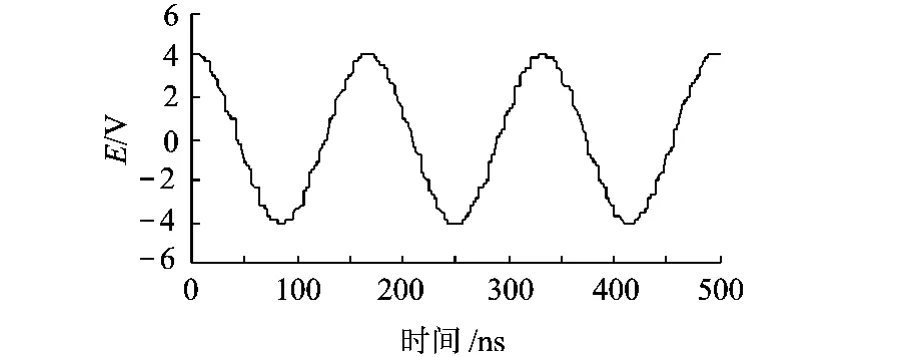
图2 非均匀采样数据曲线仿真波形
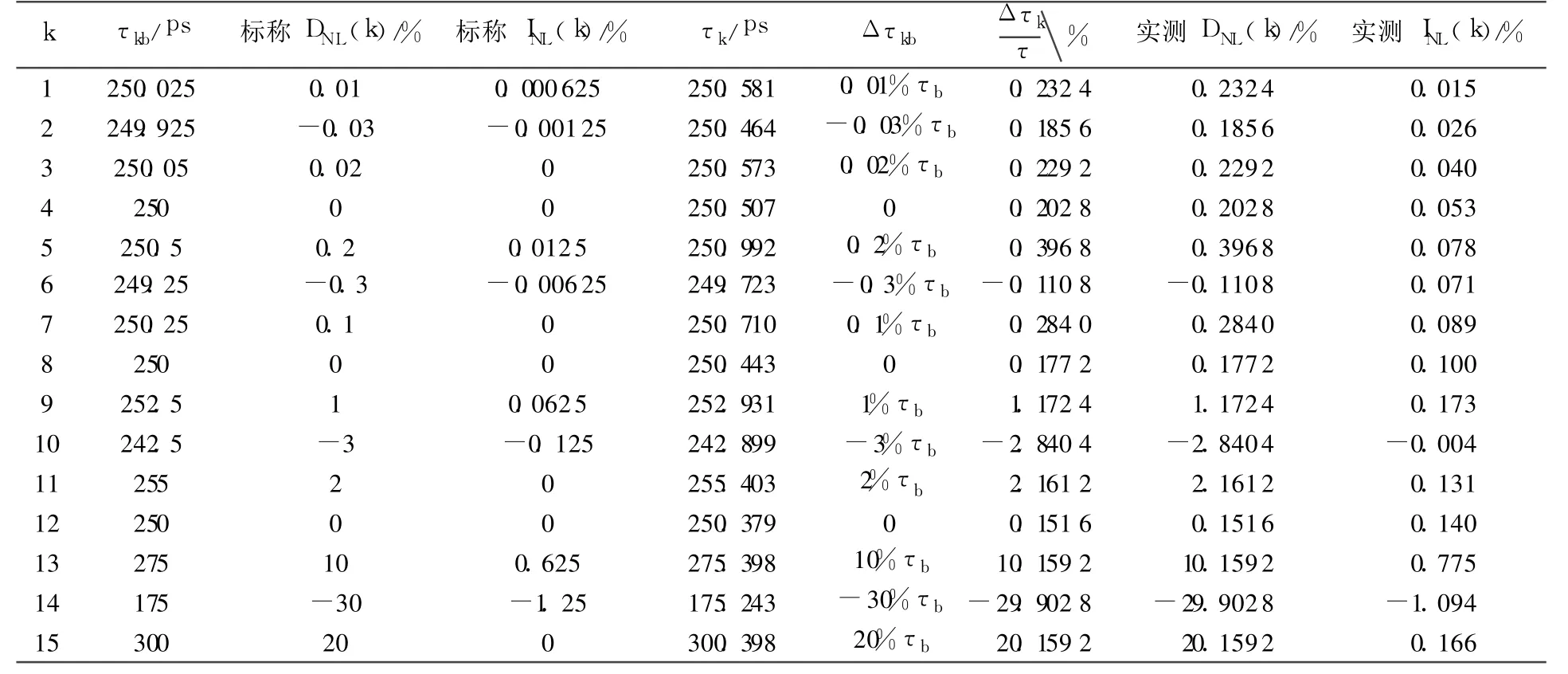
表 1 各子 A/D标称 DNL(k)和 INL(k)及测量结果
用上述方法对仿真序列{xi,i=1,2,…,n}进行二次抽样,获得 M个子序列{yk(m),m=1,2,…,n/M},经计算获得各延迟时间差 τk的测量结果见表 1,其中 ,Δτk=τk-τb,标称 INL=-1.25%,实测INL=-1.09%.
图3为表 1所述微分非线性数据曲线图,包含标称曲线和实测曲线,可见两条曲线基本重合.
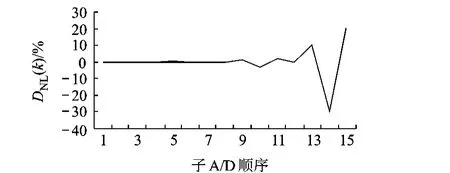
图3 微分非线性数据曲线
图4为表 1所述积分非线性数据曲线图,包含标称曲线和实测曲线,可见,两条曲线有一定差距,但变化趋势基本一致.
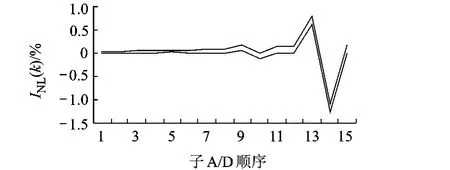
图4 积分非线性数据曲线
由仿真可见,本文方法可以用于多 A/D非均匀采样系统中各子 A/D间采样时基失真的精确测量和评价,能以微分非线性和积分非线性方式给出确切评价结果,并与实际设定值符合性良好.其中,在所述仿真条件下,积分非线性设定值与实测值之差小于 0.22%,微分非线性设定值与实测值之差小于 0.2%.
3 实测结果验证
以 TDS784D型数字存储示波器作为被测非均匀采样系统,其 A/D位数 8bits,带宽 1GHz,其时基准确度为 ±5×10-5,选取测量范围 ±5 V,v=4 GSa/s,τ=250 ps,n=60 000,信号源为HP3325B,选取 f0=6254321Hz,E=4V,其实际测量曲线波形如图 5所示.使用失真度分析手段[23],可以得到其总失真度为 1.30%,这应该包含由于非均匀采样带来的测量波形失真.
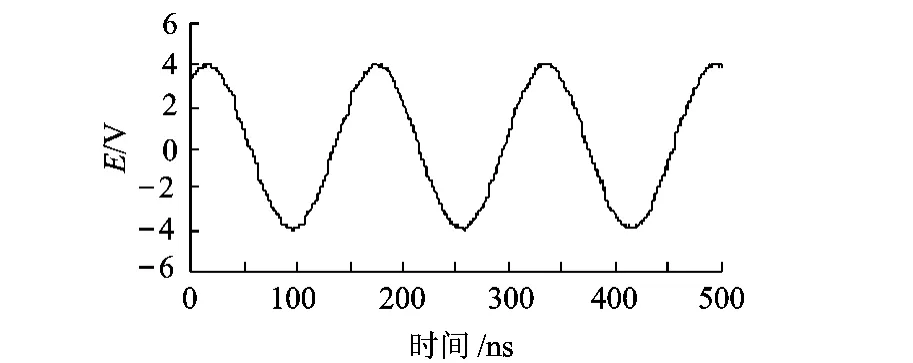
图5 数字示波器时域采样正弦波形
计算获得其实际采样速率为[23]:v=3.9999737GSa/s;
实际采样间隔:τ=1/v=250.00164ps.
已知子 A/D个数 M=4,τb=τ.按上述方法计算获得各相邻子 A/D的 DNL(k)和 INL(k)测量结果见表 2.
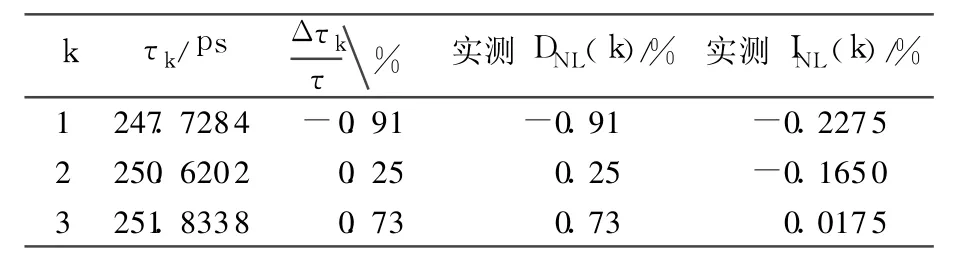
表 2 各子 A/D的 DNL(k)和 INL(k)测量结果
由测量结果可见,使用本文方法,可在实际非均匀采样系统中获得切实的技术参数,过程简洁,比较容易实现.相对于该款示波器的时基准确度±5×10-5而言,其最大的时基积分非线性-0.2275%还是非常大的失真,因而精确测量并寻求解决办法是非常必要的客观需求,因为时基失真本身不可避免地带来信号波形的测量结果失真,这也是到目前为止人们最容易忽略的一个问题,也是本文内容的价值所在.
4 结束语
本文所述内容,主要是借用了用于评价 A/D和 D/A的微分非线性与积分非线性的概念,用来评价非均匀采样系统中由于非均匀采样造成的时基失真,并称之为时基微分非线性和时基积分非线性.仿真结果表明了其在评价非均匀采样时基失真时的有效性,而在数字存储示波器上的实测结果则验证了其可行性和应用价值.
从公开文献中尚未发现有其它方法可以针对该问题获得本文所述结果,原因之一是目前其它方法多数属于频域滤波方法,很难确切分离并获得每个子 A/D的独立贡献,且能保证较高的测量准确度.由于本文方法属于模型化测量方法,使得它可以使用全序列的测量数据获取延迟参数,因此可获得较其它方法更高的延迟测量准确度,进而获得有实用意义和价值的时基非线性参数.
本文上述内容,仅仅侧重于如何有效定义和评价非均匀采样系统的时基失真,以比较不同系统时基特性的优劣,为改善和提高非均匀采样系统的性能提供方法和技术支撑.更进一步的研究内容将包括如何补偿和修正非均匀采样系统的时基失真,以便获得更加均匀的采样效果,相应工作,目前在嵌入式系统中、硬件在线补偿和实时修正研究进展较多,而对于非嵌入式系统,以软件、方法进行事后系统补偿修正的研究尚较少,有待于更深入的研究开展与进行.
References)
[1]Souders TM,Flach D R,Hagwood C,et al.The effects of tim ing jitter in sampling systems[J].IEEE Transactions on Instrumentation and Measurement,1990,39(1):80-85
[2]Wagdy M F,Awad S S.Effect of sampling jitter on some sine wave measurements[J].IEEE Transactions on Instrumentation and Measurement,1990,39(1):86-89
[3]Schoukens J,Louage F,Rolain Y.Study of the influence of clock instabilities in synchronized data acquisition ystems[J].IEEE Transactions on Instrumentation and Measurement,1996,45(2):601-604
[4]Stenbakken G N,Liu D,Starzyk JA,et al.Nonrandom quantization errors in timebases[J].IEEE Transactions on Instrumentation and Measurement,2001,50(4):888-892
[5]Kalashnikov AN,ChallisR E,Unwin M E,et al.Effectsof frame jitter in data acquisition systems[J].IEEE Transactions on Instrumentation and Measurement,2005,54(6):2177-2183
[6]Ridder F D,Pintelon R,Schoukens J,et al.Reduction of the gibbs phenomenon applied on nonharmonic time base distortions[J].IEEE Transactions on Instrumentation and Measurement,2005,54(3):1118-1125
[7]Chang C L,Huang P S,Tu TM.Aperture jitter of sampling system in AWGN and fading channels[J].IEEE Transactions on Instrumentation and Measurement,2007,56(3):831-839
[8]Souders T M,et al.IEEE Std 1057—1994,IEEE Standard for Digitizing Waveform Recorders[S]
[9]Verspecht J.Accurate spectral estimation based on measurements with a distorted-time base digitizer[J].IEEE Transactions on Instrumentation and Measurement,1994,43(2):210-215
[10]Stenbakken G N,Deyst JP.Time-base nonlinearity determination using iterated sine-fit analysis[J].IEEE Transactions on Instrumentation and Measurement,1998,47(5):1056-1061
[11]Wang CM,Hale PD,Coakley K J.Least-squares estimation of time-base distortion of sampling oscilloscopes[J].IEEE Transactions on Instrumentation and Measurement,1999,48(6):1324-1332
[12]Jenq Y C.Digital spectra of nonuniformly sampled signals:fundamentals and high-speed waveform digitizers[J].IEEE Transactions on Instrumentation and Measurement,1988,37(2):245-251
[13]Jenq YC.Digital spectra of nonuniformly sampled signals:digital look-up tunable sinusoidal oscillators[J].IEEE Transactions on Instrumentation and Measurement,1988,37(3):358-362
[14]Jenq Y C.Digital spectra of nonuniform ly sampled signals:a robust sampling time offset estimation algorithm for ultra highs peed waveform digitizer susing interleaving[J].IEEE Transactions on Instrumentation and Measurement,1990,39(1):71-75
[15]Attivissimo F,Nisio A D,Giaquinto N,et al.Measuring time base distortion in analog-memory sampling digitizers[J].IEEE Transactions on Instrumentation and Measurement,2008,57(1):55-62
[16]Barford L.Filtering of random ly sampled time-stamped measurement[J].IEEE Transactions on Instrumentation and Measurement,2008,57(2):222-227
[17]Jeng YC,Cheng L.Digital spectrum of a nonuniform ly sampled two-dimensional signal and its reconstruction[J].IEEE Transactions on Instrumentation and Measurement,2005,54(3):1180-1187
[18]Kazakov V A,Rodriguez D S.Sampling-reconstruction procedure of Gaussian processes with jitter characterized by the beta distribution[J].IEEE Transactions on Instrumentation and Measurement,2007,56(5):1814-1824
[19]Deyst JP,Souders T M,Solomon O M J.Bounds on leasts quares four-parametersine-fiterrorsdue to harmonic distortion and noise[J].IEEE Transactions on Instrumentation and Measurement,1995,44(3):637-642
[20]梁志国.通道间延迟时间差的测量不确定度[J].计量学报,2005,26(4):354-359 Liang Zhiguo.The measurement uncertainty of delay between channels[J].Acta Metrologica Sinica,2005,26(4):354-359(in Chinese)
[21]Liang ZG,Zhu J J.A digital filter for the single frequency sinusoid series[J].Transaction of Nanjing University of Aeronautics&Astronautics,1999,16(2):14-16
[22]梁志国,朱济杰,孙璟宇.正弦信号总失真度的一种精确评价方法[J].计量学报,2003,24(2):144-148 Liang Zhiguo,Zhu Jijie,Sun Jingyu.A precisely evaluation method of the distortion of sine wave signalgenerators[J].Acta Metrologica Sinica,2003,24(2):144-148(in Chinese)
[23]梁志国,周艳丽,沈文.正弦波拟合法评价数据采集系统通道采集速率[J].数据采集与处理,1997,12(4):328-333 Liang Zhiguo,Zhou Yanli,Shen Wen.Using sinuous curve-fitting method to evaluate the rate of data acquisition systems[J].Journal of Data Acquisition&Processing,1997,12(4):328-333(in Chinese)
(编 辑:刘登敏)
Novelevaluation method of time base distortion of nonuniformly sampling data acquisition systems
Liang Zhiguo Meng Xiaofeng
(School of Instrument Science and Opto-electronics Engineering,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)
By using both the time base differential non-linearity and integral non-linearity,a novel method to evaluate the time base distortion is presented,which deal with the nonuniform ly sampling data acquisition systems.By using sinusoidal stimulating,and then re-sampling the data to create sub-series of each sub-A/D converter,through curve-fit results of sub-series sinusoidal waveforms,the phase difference between two subseries was obtained.The time difference corresponding the phase difference is the sampling time delay between two sub-A/D.Their consistency is the time base distortion of nonuniformly sampling systems,which can be expressed in time base difference non-linearity and time base integral non-linearity.In simulation test,the correctness of the method was validated.In practical experimenton a digital storage oscilloscope,the feasibility of the method was proved.The method above can be use to evaluate the time base distortion of nonuniformly sampling data acquisition systems.
time base;distortion;nonuniformly sampling;curve-fit;calibration;evaluation
TM 930.114
A
1001-5965(2010)10-1203-04
2009-09-14
梁志国(1962-),男,黑龙江巴彦人,博士生,lzg304@sina.com.

