旋翼多维振动最优调整方法
王 康 王少萍
(北京航空航天大学 自动化科学与电气工程学院,北京 100191)
刘红梅
(北京航空航天大学 可靠性与系统工程学院,北京 100191)
旋翼多维振动最优调整方法
王 康 王少萍
(北京航空航天大学 自动化科学与电气工程学院,北京 100191)
刘红梅
(北京航空航天大学 可靠性与系统工程学院,北京 100191)
针对直升机旋翼系统非线性、难以建模的特点,采用径向基函数(RBF,Radial Basis Function)神经网络建立直升机旋翼动平衡调整模型.根据约束条件以直升机机身振动值作为目标函数建立适应度函数,以旋翼系统的调整参数为优化变量,进行神经网络学习和优化.利用粒子群优化(PSO,Particle Swarm Op timization)算法对适应度函数进行寻优,获得当直升机振动最小时的桨叶的调整参数.实验结果表明:PSO算法寻优效率方面高于遗传算法;RBF神经网络和 PSO算法相结合可以有效地实现直升机旋翼动平衡调整.
旋翼;径向基函数;粒子群优化;优化
直升机机身的大幅度振动不仅使机组人员和乘客感到疲劳,也会使直升机大量元部件产生高度疲劳,降低武器系统性能(导弹瞄准困难).直升机振动抑制问题一直倍受关注,因此对直升机旋翼的动平衡调整研究就尤为重要[1]
当旋翼出现动不平衡以后,一般是通过调整旋翼系统的平衡片、桨叶后缘调整片和桨叶变距拉杆来达到平衡的目的,但是如何优化调整该三者,以减少直升机的振动,是目前一个较新的研究方向.
在动平衡问题上,一直采用测量振动的方法.最初一般采用传统的转子动平衡方法,将旋翼系统看成一个整体,在此基础上进行质量不平衡调整,该方法适合 0.2g以上直升机,对于以低振动水平为代表的第 4代直升机,该方法就不适用了.为此,国外重点发展了神经网络分析方法.典型的代表有:欧直公司的 STEADYCOPTER,美国马里兰大学阿尔佛雷德·杰斯福旋翼机中心等[2-3].
本文采用径向基函数(RBF,Radial Basis Function)网络建立起旋翼系统调整参数与机身振动信号之间的非线性模型;采用粒子群优化(PSO,Particle Swarm Optimization)算法对适应度函数进行寻优;结合 RBF和 PSO实现旋翼系统动平衡调整.
1 旋翼动平衡调整系统分析
直升机的振动是通过传感器采集多个测点的振动信号,并将多个信号进行信息融合来实现的.振动传感器应安装在直升机上对不平衡振动敏感的位置,机身共安装 6个传感器,安装在旋翼轴和主副驾驶员处,可以感知 6个方向的振动量.测量机身振动值时考虑直升机飞行的 4个状态:地面开车、低空悬停、低速飞行和高速飞行.另外,考虑到振动数据具有幅值和相位,为方便计算,将各方向的振动数据转化到二维笛卡尔坐标系中.由上述论述可知,通过振动传感器可以采集直升机机身在不同飞行状态下的 48个振动值.
当旋翼出现动不平衡以后,一般是通过调整旋翼上的平衡片、桨叶后缘调整片和桨叶变距拉杆来达到减少直升机振动,保持机身平衡的目的.本文以 3片桨叶的直升机为例,其中有 1片桨叶是固定的,无法调整的.另外 2片桨叶可以分别调整平衡片、桨叶后缘调整片和桨叶变距拉杆.因此,旋翼的动平衡调整可以通过 6个调整参数来实现.旋翼动平衡调整原理如图 1所示.

图1 旋翼动平衡调整原理
从图 1看出,采用 RBF神经网络建立了旋翼系统调整参数与机身振动量之间的数学模型.根据 RBF神经网络,输入不同的旋翼调整参数,得到机身振动值.以机身振动值为目标函数确立适应度函数,并利用 PSO对适应度函数进行优化,得到一个最优的旋翼调整参数,以此调节相应的参数减小直升机机身的振动.
2 旋翼动平衡调整系统建模
根据上述直升机旋翼系统的分析可知,旋翼系统是通过改变 6个调整参数使机身的 48个振动值达到指定要求.由于直升机旋翼系统结构复杂,机身振动值受各方面耦合因素影响很大,旋翼系统的调整参数与机身振动量之间成非线性关系.采用一般线性系统建模很难准确地表征旋翼系统的调整参数与机身振动量之间的关系.
RBF神经网络一般采用高斯函数作为基函数,使用最小二乘准则作为目标函数,使用梯度下降法来迭代调节每个节点的参数[1].RBF神经网络具有很多优点:收敛速度很快、网络规模较小、计算量较小等等.鉴于这些特点,选取 RBF神经网络建立旋翼系统的调整参数与机身振动量之间的模型.
整个 RBF神经网络,输入层为 6个节点、输出层为 48个节点、隐节点个数为 42个(如图 1所示).RBF神经网络的输入为各调整参数 αji(其中i代表桨叶序列号 1,2;j代表参数类型:1为桨叶后缘调整片,2为平衡片,3为桨叶变距拉杆),神经网络的输出为传感器采集的 48个振动值.
2.1 优化动量因子的神经网络数学模型
RBF神经网络建立起旋翼系统调整参数与机身振动值之间的模型.神经网络由 3层组成.
RBF神经网络的输出值为

式中,W=[w1,w2,…,wn]为网络的权值向量;H=[h1,h2,…,hm]为径向基函数,采用高斯函数[4]:
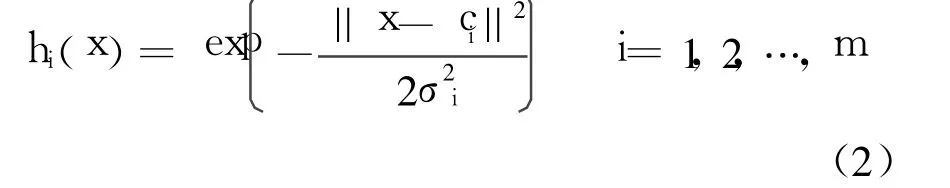
式中,x为 n维输入向量;ci为第 i个基函数的中心;σi为第 i个函数的宽度参数;m为隐节点的个数.
权值调整采用梯度下降算法[5],其迭代公式为


式中,η为学习率;α,β,χ为动量因子.α,β,χ对神经网络训练精度影响很大.选取 67535个样本点对神经网络的精度进行验证,当 α,β,χ分别取10-1,10-2,10-3时,神经网络的误差曲线如图 2~图 4所示.选择不同的值时,神经网络训练的精度有所不同.

图2 α,β,χ取 10-1

图3 α,β,χ取 10-2

图4 α,β,χ取 10-3
通过比较可以看出,α,β,χ取值为 10-2时,神经网络训练误差最小.
2.2 动平衡调整目标函数的确定
动平衡调整目标函数的选取不仅要考虑机身振动值最小,还应考虑旋翼系统的调整参数不应过大,因此优化目标函数的确定要考虑以下两个因素:机身振动值和旋翼系统的调整参数.
以机身振动值最小为目标函数,以旋翼系统的调整值为优化变量,进行网络学习和优化,通过寻优获得机身振动值最小时旋翼系统调整参数.选取目标函数为


根据直升机机体对振动的要求,直升机座舱和旋翼主轴的各方向振动应小于定值 K,即

式中,K=0.2.
2.3 优化问题的转换
式(9)建立了目标函数,式(11)确定了约束条件.以下将采用 PSO对目标函数进行寻优.由于 PSO不能直接处理约束条件,因此采用罚函数法[6]将约束问题转化为无约束问题.优化目标函数为

3 PSO与 RBF结合优化调整参数
RBF神经网络建立的是旋翼系统调整参数和机身振动值之间的模型,通过改变旋翼系统的调整参数使机身的振动达到最小.这就要求旋翼系统调整值和机身振动值之间是一一对应关系,因此必须论证 RBF神经网络函数的单调性.
3.1 单调性论证

对式(13)两边同时求导,可得


3.2 PSO与 RBF结合优化
采用 RBF神经网络建立旋翼系统调整参数与直升机机身振动信号之间的数学模型.根据RBF神经网络输入的不同的旋翼系统调整参数,得到直升机机身振动值,以机身振动值为目标函数确立适应度函数,并利用 PSO对适应度函数进行优化,得到一个最优的旋翼调整参数,以此调节相应的参数减小直升机机身的振动.通过 1到2次飞行调整,使直升机机身振动为最小,完成旋翼系统的动平衡调整.图 5为旋翼系统调整参数的寻优流程.

图5 PSO寻优流程图
4 实例分析
4.1 旋翼动平衡调整前后机身振动值比较
采用 RBF与 PSO相结合的旋翼动平衡调整算法对直升机机身振动值进行优化,其调整前后机身振动值对比如图 6所示.
根据旋翼动平衡调整的要求,调整后机身振动值应小于 0.2,从图 6中可看出经过动平衡调整,振动水平大大地降低了,机身振动值都在 0.1以下,达到了调整要求.其中图 6中横坐标为 4个飞行状态下 6个传感器测得的机身振动数据.
要得到图 6中的机身振动值,需对直升机旋翼做出相应调整,旋翼调整参数如表 1所示.

表 1 获得机身最小振动的旋翼调整参数

图6 PSO调整前后振动值对比
4.2 PSO与遗传算法比较
为了说明 PSO的优越性,分别采用遗传算法和 PSO对目标函数进行优化.
遗传算法和粒子群的种群规模均选择为 150个,最大迭代次数选取 n=500次.其寻优过程如图 7所示,可以看出,采用遗传算法,目标函数寻优到第 430代,才找到全局最优点.而图 8中的PSO 120次就能寻找到全局最优点.通过比较可以看出,PSO的寻优效率高于遗传算法.
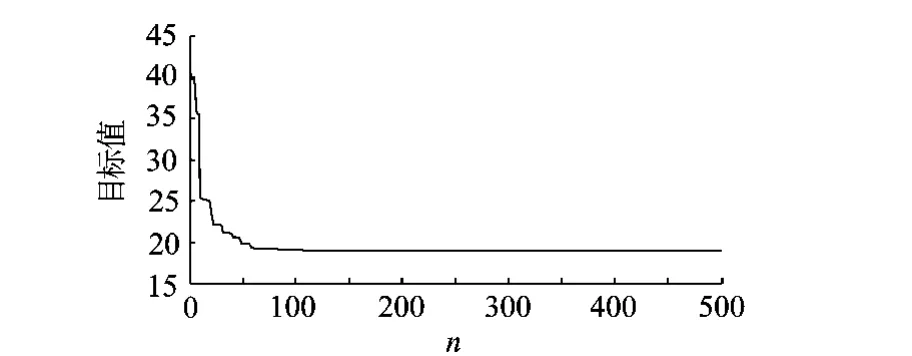
图7 PSO寻优过程

图8 遗传算法寻优过程
这是因为:①粒子具有记忆的特性,通过学习使其下一代从前辈继承更多信息[7];②遗传算法全局搜索能力很强,而局部搜索能力相对较弱;③PSO没有遗传、交叉等操作,其计算的复杂度要比遗传算法要低.
从迭代次数来看,PSO比遗传算法具有很多优越性.因此,选取 PSO与 RBF神经网络相结合来实现直升机旋翼动平衡调整.
5 结 论
根据旋翼模型的非线性特点,采用 RBF神经网络建立旋翼动平衡调整的模型,确定适应度函数,并采用 PSO对适应度函数进行寻优,确定了获得最小振动值时旋翼系统调整参数.实验数据和分析结果表明:①根据 PSO与 RBF相结合的方式来优化旋翼系统调整参数,可以大大地减小机身振动值;②调整效率高,RBF神经网络与 PSO相结合能够在较少飞行调整下完成旋翼动平衡调整;③PSO寻优效率方面高于遗传算法.
References)
[1]薛伟松,邢士喜,郑牧,等.直升机旋翼锥体及动平衡设备校验系统的研究[J].测控技术,2006,25(3):4-7 XueWeisong,Xing Shixi,Zheng Mu,et al.Research on checkout system for track-height and dynamic balance equipment of helicopter[J].Testing and Control Technology,2006,25(3):4-7(in Chinese)
[2]Ventres Sam,Hayden Richard E.Rotor tuningusing vibration data only[C]//American Helicopter Society 56th Forum.Alexandria:American Helicopter Society,2000:623-629
[3]Wang Shengda,Danai Kourosh,Wilson Mark.Adaptive method of helicopter track and balance[J].Journal of Dynamic Systems,Measurement,and Control,2005,127(6):275-282
[4]袁海文,吕弘,袁海斌.基于 RBF神经网络的控制电器元件故障诊断[J].北京航空航天大学学报,2006,32(5):544 547 Yuan Haiwen,LǜHong,Yuan Haibin.Fault diagnosis of control electric component based on RBF neural network[J].Journal of Beijing University of Aeronautics and Astronautics,2006,32(5):544-547(in Chinese)
[5]Liu Hongmei,Wang Shaoping,Ouyang Pingchao.Fault diagnosis in a hydraulic position servo system using RBF neural network[J].Chinese Journal of Aeronautics,2006,19(4):346-353
[6]李炳宇,萧蕴诗,江镭.PSO算法在工程优化问题中的应用[J].计算机工程与应用,2004(18):74-76 Li Bingyu,Xiao Yunshi,Jiang Lei.Application of particle swarm optimization in engineering optimization problem[J].Computer Engineering and Applications,2004(18):74-76(in Chinese)
[7]乔维德.基于改进粒子群算法神经网络的电力电子电路故障诊断[J].电气传动自动化,2008,30(5):29-31 Qiao Weide.Fault diagnosis of power electronic circuits based on improved PSO algorithm neural network[J].Electric Drive Automation,2008,30(5):29-31(in Chinese)
(编 辑:刘登敏)
Optimalad justment method of rotormulti-dimensional vibration
Wang Kang Wang Shaoping
(School of Automation Science and Electrical Engineering,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)
Liu Hongmei
(School of Reliability and Systems Engineering,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)
Considering characteristics of non-linear and difficult to model for the rotor system,helicopter rotor dynamic balancing adjustment models was established by radial basis function(RBF)neuralnet work.According to the constraints,the fitness function was established by using the helicopter vibration as objective function and the optimization variables were used by the adjustment parameters of rotor.The radial basis function neural net work learning and optimization were used by the helicoptervibration and the adjustment parameters of rotor.Particle swarm optimization(PSO)algorithm was used to make a global optimization to find the suitable rotor adjustments corresponding to the minimum vibrations.The experimental results indicate that the particle swarm optimization algorithm is higher than the genetic algorithm in the aspect of efficiency optimization and the radial basis function combined with the particle swarm optimization algorithm can effectively achieve the helicopter rotor dynamic balance adjustment.
rotor;radial basis function;particle swarm optimization;optimization
TP 273+.23
A
1001-5965(2010)11-1303-04
2009-09-28
王 康(1984-),男,山东莱州人,博士生,wangkang14team@163.com.

