用于识别双星故障的 RAIM算法
赵 琳 李 亮 程建华 娄上月
(哈尔滨工程大学 自动化学院,哈尔滨 150001)
用于识别双星故障的 RAIM算法
赵 琳 李 亮 程建华 娄上月
(哈尔滨工程大学 自动化学院,哈尔滨 150001)
由于传统的基于识别门限的卫星故障识别算法存在漏检和误警致使识别率较低,为此提出一种可用于识别双星故障的接收机自主完好性监测算法.该算法通过构造新的奇偶矢量与故障特征平面,利用奇偶矢量与故障特征平面之间的几何关系来识别卫星故障,使得算法不再受限于识别门限的影响,从而有效地避免了由于识别门限引起的识别效率较低的问题.计算机仿真结果表明:改进后的算法与传统的基于识别门限的算法相比,双星故障正确识别的性能有显著的提高,正确识别率可达到 90%.同时,与基于门限识别的重构最优奇偶矢量法相比,计算量可减少约 61.2%以上.
卫星导航;接收机自主完好性监测;故障识别;故障特征平面;奇偶矢量
目前,完好性监测有两种典型的实现方式:一种是 GPS完好性通道(GIC,GPS Integrity Channel).GIC通过地面监测站采集观测数据集中处理,并将产生的完好性信息通过地球同步卫星播发给其覆盖的用户.虽然 GIC具有对故障快速反应和覆盖范围广等优点[1],但是 GIC系统实现复杂,且维护费用昂贵,因此其应用有一定的局限性.另一种是接收机自主完好性监测(RAIM,Receiver Autonomous Integrity Monitoring),RAIM由于其自主性强、算法实现较为简单等优点而逐渐成为完好性监测算法的主要研究方向[2-3],而如何快速有效地检测与识别卫星故障,一直是RAIM算法中的研究热点之一[4-6].早期关于RAIM中故障识别的研究大多基于单星故障,然而,随着我国“北斗”二代计划的实施,可用于定位的卫星星座也随之增多,因此多颗卫星发生故障的概率,尤其是双星同时发生故障的概率不可忽视.
目前 RAIM算法中用于识别多卫星故障的方法之一是基于历史观测量的“串行(sequential)”算法,“串行”算法具有利用时域信息来弥补卫星观测量不足的特点.例如文献[7]提出利用卡尔曼滤波产生的新息进行故障识别.虽然该算法通过结合时域与集合一致性检测的互补特性,提高了多故障识别率,然而其故障识别性能依赖于先验误差估计的准确性,而且检测速度较慢,故而没有被普遍采用.另一种较为典型的多故障识别算法是“快照(snapshot)”算法,例如文献[4]和文献[6]分别提出假设验证法和重构奇偶矢量法用于双星故障识别,极大地提高了故障识别的性能.但是两者都是基于识别门限进行故障识别,而且为弥补观测噪声对识别效率的影响,只能利用调节系数对识别门限进行保守调整以防止漏检.然而识别门限的调整必然会影响故障识别的性能和计算量.另外,当可视卫星数较多或较少时,调节系数的设置成为算法另一个需要解决的问题.
本文首先分析了传统基于识别门限的故障识别算法存在的不足,然后提出了一种不受识别门限影响的“快照”算法,即通过判断所构造的奇偶矢量和故障特征平面之间的几何关系识别双星故障,有效提高双星故障识别的性能.
1 传统故障识别算法存在的不足
由卫星导航系统定位原理可得如下量测方程:

式中,Y为 n维残差观测量;G为 n×m维观测矩阵;X为 m维未知量(包括位置修正量、钟差等),∈为 n维残差观测量中所包含的噪声,且 ∈~N(0,σ2),σ为伪距观测量标准差;b为 n维卫星故障向量,若无故障发生,则 b为零向量,否则为非零向量.
对 G进行奇异值分解有[8]




图1 双星故障导致漏检

图2 双星无故障导致误警
从图 1可以看出,利用识别门限识别故障时,两个故障矢量在奇偶变换矩阵的作用下可引起漏检.文献[6]分析了产生漏检的原因,并建议采用重构最优奇偶矢量结合符号判断避免漏检.但是文献[6]中提出的重构最优奇偶矢量是在忽略观测噪声的前提下构造的,为补偿观测噪声的影响,只能通过调节系数调整识别门限以防止漏检,这使得识别算法的效率有所降低,而且当实际观测噪声较大时,算法的识别性能必然受到影响.因此有必要构造充分考虑到观测噪声影响的奇偶矢量以提高算法的可靠性.从图 2可以看出,采用识别门限进行故障识别时,两个无故障矢量在奇偶变换矩阵的映射下有可能会导致误警.
通过以上分析可知,采用传统的基于识别门限的算法识别双星故障容易导致漏检和误警,因此必须采用新的双星故障识别算法提高双星故障RAIM算法的适用性.
2 改进的双星故障识别算法
结合式(1)、式(3)可知:

将式(5)分解可得


将式(7)重组有


为了方便讨论所构造的奇偶矢量在识别卫星故障上的可行性,暂时忽略观测噪声的影响.首先考虑单星故障的情况,假设第 i颗卫星发生故障,即卫星故障向量 bi不为零,则由式(9)有

类似的,假设第 i,j颗卫星发生故障,即卫星故障向量 bi和 bj不为零,由式(9)有

从式(11)可以看出,当出现双星故障时,卫星故障偏差也是通过奇偶空间矩阵的每一列反映到 p中的,但此时 p不再与的某一列成比例了,因此单星故障识别的思想不再适用.但仍可利用奇偶矢量与奇偶空间矩阵之间的几何关系识别卫星故障,即如果发生双星故障,那么奇偶矢量应该位于向量,i)和j)所构成的平面上,本文称之为故障特征平面.考虑到观测噪声的影响,如果奇偶矢量与故障特征平面之间的夹角约为 0,则可判断构成故障特征平面的故障特征向量所对应的双星组合发生故障.通过这种几何判断算法,有效解决双星故障识别中受识别门限影响的问题,从而避免漏检与误警的发生.
通过以上分析可知,正是基于奇偶矢量与故障特征平面之间的几何关系,才使得构造奇偶矢量实现双星故障识别成为可能.为方便阐述双星故障识别算法,先定义如下概念.
定义归一化的故障特征向量为

定义由故障特征向量构成的故障特征平面S,以第 i,j颗卫星的故障特征向量为例,表示如下:

p在故障特征平面 S的投影为 p⊥,则 p与 S之间的夹角 θ即为 p与 p⊥之间的夹角,即


当且仅当 p与 p⊥完全重合时,等号成立,此时 θ=0,因此当 p位于故障特征平面 S上时,可判断构成此故障特征平面的故障特征向量所对应的卫星已经发生故障.显然,通过式(14)可以简化故障识别的计算量.
由于 p⊥位于和所构成的故障特征平面上,即 p⊥∈ Si,j,则和线性相关,即p⊥可由和线性表出,可表示为
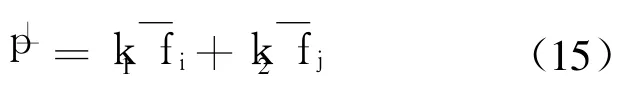

当前卫星集通过 RAIM可用性检测后,方可进行故障的检测与识别.至此,可将双星故障检测与识别算法的流程介绍如下:
1)对 G做奇异值分解,得到 U2;
4)遍历 n个故障特征向量中任意两个故障特征向量构成的故障特征平面 Si,j(共个),由式(15)计算出每个 Si,j所对应的 p⊥;
5)结合式(14)和步骤 4)所得到的 p⊥计算,则可判断第 i,j颗卫星发生故障.
本文所提出的双星故障识别算法无需设定识别门限,使得算法的识别性能有所提高,计算量有所降低,能够有效避免故障识别中的误警和漏检.需要说明的是,实际工程应用中,在双星故障识别之前,需要检测当前卫星故障是单星故障还是双星故障,只有在检测到双星故障之后,才能进行双星故障的故障识别.
3 仿真结果
3.1 故障识别率比较
为验证本文所提出的改进的双星故障识别算法,利用 Matlab对 GPS卫星定位系统中存在双星故障卫星时算法的性能进行了仿真.其中 GPS星座模拟采用 GPS仿真软件包(Satellite Navigation Toolbox for Matlab)中提供的 svprime.dat和mops24.dat两个数据文件.用户位置在地球表面均匀选取;每 2h采样一次.为更好地与最优奇偶矢量法比较,仿真中故障卫星的卫星号是随机产生的,σ=4m,卫星截止高度角为 7.5°,误警率为0.001.由文献[3]可知,为有效检测并识别双星故障,至少需要 7颗卫星.在通过可用性检测之后,对不同的双星组合分别加入不同的卫星故障偏差,总共进行 7200次 Monte-Carlo仿真,分别比较了基于识别门限的常规奇偶矢量、重构最优奇偶矢量(其中识别门限中的调节系数取0.95)以及本文所提出的改进算法的双星故障识别性能,仿真结果如图 3~图 5所示.
图3~图 5中,x,y坐标轴分别表示两颗卫星故障上故障幅值与 σ的比值.仿真中对所有两颗卫星分别加上 -10σ~-3σ,3σ~10σ的故障偏差(伪距观测量中所包含的故障幅值一般以 3σ为门限[6]).

图3 两颗故障卫星下常规奇偶矢量的故障识别率

图4 两颗故障卫星下重构最优奇偶矢量的故障识别率

图5 两颗故障卫星下改进算法的故障识别率
由图 3可以看出,由于传统算法进行故障识别容易引起误警和漏检,因而即使故障偏差较大时故障识别率仍然很低.
从图 4可以看出,重构最优奇偶矢量法在用于两颗卫星故障识别时,改进了传统算法在局部识别率低的问题,但是识别性能有待于提高,原因在于本次仿真中故障识别的卫星数并不是固定的,而固定的调整系数影响了故障识别的性能.
由图 5可知,本文提出的改进算法所构造的奇偶矢量用于识别双星故障时,故障正确识别率可高于 90%,当故障偏差较大时,故障正确识别率高达 99%左右,充分说明了改进算法在识别双星故障上的优越性.
3.2 计算量比较
文献[4,6]提出的算法需要提前设定调节系数 f以降低漏检率.在可用卫星数目较少时,f对故障识别效率的影响较小,但是当卫星数目较多时,f决定了需要重新进行故障识别的卫星组的数目,因而增加了故障识别的计算量.常规算法是指基于识别门限利用常规奇偶矢量进行故障识别.在可见卫星为 12颗时,取 100次正确识别故障时间的平均值作为单次故障识别时间.3种算法计算量比较结果如表 1所示.仿真所使用计算机主频为 2.5GHz.

表 1 各算法的计算量比较
由表 1可见,本文所提出的改进算法计算量略高于传统算法,但识别性能却大大高于传统的算法,实用性较好.为了突出 f对计算量的影响,表 1给出了在不同 f条件下重构奇偶矢量法的计算量,当 f分别取 0.95,0.90和 0.85时,本文所提出的算法的计算与重构最优奇偶矢量法相比,计算量分别减少约 61.2%,68.7%和 74.4%,原因在于随着 f的减小,虽然可以有效地抑制漏检,但需要重新识别的卫星组合也越多,导致故障识别的计算量也急剧增加.虽然这里列出的相对CPU时间没有绝对意义,但还是从时间层面上反映了本文所提出的改进算法更有益于工程实现.
4 结 论
随着可用于定位的卫星系统的增多,传统基于识别门限的双星故障识别算法性能太差,已经不能适应现代卫星导航系统完好性监测性能的需求.本文提出的双星故障识别“快照”算法可获得90%以上的故障识别率.与重构最优奇偶矢量法相比,本文提出的改进算法避免了调节系数对识别门限的影响,计算量可减少约 61.2%以上,为双星故障识别 RAIM算法的工程实现提供了新的思路.
References)
[1]Brown R G.RAIM and GIC working together:the ultimate solution to the GPS integrity problem[J].Navigation,1989,36(2):173-178
[2]陈金平.GPS完善性增强研究[D].郑州:解放军信息工程大学测绘学院,2001 Chen Jinping.Research of GPS integrity augmentation[D].Zhengzhou:Institute of Surveying and Mapping,Information Engineering University,2001(in Chinese)
[3]Martini I,Hein GW.An integrity monitoring technique formultiple failures detection[C]//IEEE/ION Position,Location,and Navigation Symposium.San Diego,CA,United Statues:Institute of Navigation,2006:450-467
[4]张强,张晓林,常啸鸣.用于卫星导航多星故障识别的新方法[J].航空学报,2008,29(5):1239-1244 Zhang Qiang,Zhang Xiaolin,Chang Xiaom ing.New method for satellite navigation identifying simultaneousmulti-faulty satellites[J].Acta Aeronautica et Astroautica Sinica,2008,29(5):1239-1244(in Chinese)
[5]Brown R G.Solution of the two-failure GPSRA IM problem under worst-case bias conditions:parity space approach[J].Navigation,1997,44(4):425-432
[6]张强,张晓林,常啸鸣.用于识别两颗故障卫星的 RAIM算法[J].北京航空航天大学学报,2008,34(7):773-777 Zhang Qiang,Zhang Xiaolin,Chang Xiaom ing.RAIM algorithm for identifying simultaneous two-faulty satellites[J].Journal of Beijing University of Aeronautics and Astronautics,2008,34(7):773-777(in Chinese)
[7]孙国良,孙明菡,陈金平.时-集综合的接收机自主完好性监测方法研究[J].航空学报,2006,27(6):1171-1175 Sun Guoliang,Sun Minghan,Chen Jinping.A study on time and set combinedmethod for receiver integrity[J].Acta Aeronautica et Astroautica Sinica,2006,27(6):1171-1175(in Chinese)
[8]van Diggelen F,Brown A.Mathematical aspects of GPSRAIM[C]//IEEE Position Location and Navigation Symposium.Las Vegas,United States:IEEE,1994:733-738
[9]Boris S P,David G L,Parkinson BW.Autonomous fault detection and removal using GPS carrier phase[J].IEEE Trans on Aerospace and Electronic Systems,1998,34(3):897-906
(编 辑:赵海容)
New RAIM algorithm for identifying simultaneous double-faulty satellites
Zhao Lin Li Liang Cheng Jianhua Lou Shangyue
(The College of Automation,Harbin Engineering University,Harbin 150001,China)
Because the traditional algorithms of satellite fault identification based on identifying threshold led to missed detection and false alarm,which reduced the correct identifying ratio,a new receiver autonomous integrity monitoring(RAIM)approach was proposed for identifying simultaneous double-faulty satellites.The geometry relation ships bet ween the proposed parity vector and faulty feature plane were used to identify the faulty satellites.Therefore the proposed algorithm was immune to the problem of identifying threshold and improved the correct identifying ratio.Computers imulation results indicate that compared with the existing traditional algorithms based on identifying threshold,the performance of faulty identification has a significant improvement,under the condition of simultaneous double-faulty satellites.With the proposed algorithm,the correct identifying ratio is a shigh as 90%.Moreover,compared with the reconstructed optimal parity vector algorithm based on identifying threshold,the new algorithm reduces more than 61.2%of the computational burden.
global positioning system;receiver autonomous integrity monitoring(RAIM);fault identification;faulty feature plane;parity vector
TN 967.1
A
1001-5965(2010)11-1261-05
2009-10-09
国家自然科学基金资助项目(60974104);船舶工业国防科技预研基金资助项目(08J3.8.8)
赵 琳(1968-),男,黑龙江哈尔滨人,教授,zhaolin@hrbeu.edu.cn.

