脉冲爆震火箭发动机喷管构型数值研究

李建玲，范玮，李强，严传俊

（西北工业大学动力与能源学院，西安710072）

1 引言

脉冲爆震火箭发动机[1,2](Pulsed Detonation Rocket Engine,简称PDRE)是1种利用周期性爆震波发出的冲量产生推力的非稳态新型推进系统。由于PDRE具有热效率高、结构简单、尺寸小、质量轻、工作范围广等诸多潜在优势，目前世界很多国家都对PDRE开展了研究。排气喷管是PDRE的重要部件之一，对于提高PDRE的推进性能起着非常重要的作用。对于常规液体火箭发动机等以稳态方式运行的喷气发动机而言，排气喷管技术已经比较成熟。但是，PDRE的非稳态运行特点对排气喷管的设计、选取和分析研究带来了挑战性难题，至今还没有发展出能够指导PDRE排气喷管设计的理论[3]。由于喷管构型、推进剂、初始条件等研究条件存在差异，对于喷管效用的研究结论也不尽相同，甚至出现一些相互矛盾的情况[4]。

本文采用准1维数值模型，研究了喷管构型对PDRE单次爆震过程流动以及排气性能的影响。

2 控制方程和计算方法

这里首先指出，PDRE零维模型是经典的热力循环分析模型，可以反映出爆震室内的初始压力、初始温度以及混合物当量比等主要影响因素对其性能的影响，虽然计算量小，但无法考虑波的相互作用以及非稳态流动过程对PDRE性能的影响；采用多维模型估算出的PDRE性能更可靠，但计算量显著增加。而本文所采用的准1维模型，则考虑了PDRE大部分的实际工作过程，计算量适中，可用于快速评估PDRE的推进性能，为PDRE排气喷管选择提供参考。

采用单进程变量化学反应模型，忽略气体黏性、导热以及扩散运动，描述爆震燃烧化学反应过程的准1维Euler方程为

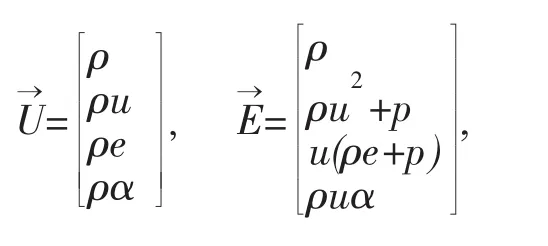
式中：γ为比热比；q为单位质量反应物放热量；w˙为反应产物的质量生成速率，用Arrhenius形式表示为

式中：K、Ea、R、T分别为化学反应的指前因子、单位质量反应物的活化能、气体常数和温度。温度T由理想气体状态方程给出

对于化学反应流计算，尤其是爆震问题，化学反应的特征时间（通常微秒量级）往往比流动特征时间小几个数量级。这使得控制方程具有了强刚性，给数值求解控制方程组带来困难。利用2阶精度Strang算子分裂法[5]来分离刚性源项，将原来的控制方程组（式（1））分裂成2个方程组：1个描述流场的齐次偏微分方程组（含非刚性源项）和另1个描述化学反应的常微分方程，对每个方程组采用不同方法进行积分求解。采用AUSM格式[6,7]进行空间离散，将无黏通量分裂为对流通量项及压力通量项来处理。时间离散采用3阶TVD龙格－库塔格式[8]。采用多步隐式方法离散含刚性化学源项的常微分方程，对所得到的非线性方程利用Newton-Raphson迭代方法求解。

此外，在控制方程中，涉及到与化学热力学和化学动力学相关的5个参数（γ，R，q，Ea，K）。对于化学恰当比的氢氧混合物（2H2+O2），这5个参数参照文献[9]、[10]给出。

3 物理模型和边界条件

本文研究的4种PDRE构型均为1端封闭、1端敞口。选作基准构型的理想PDRE为不带喷管的均匀直管，爆震管内径为40 mm，长度为200 mm。3种带喷管的PDRE构型如图1所示，爆震管内径为40 mm，长度为200 mm，喷管长度均为30 mm。在图1（a）中，收敛喷管出口直径为32 mm，喷管面积比为0.8；在图1(b)中，扩张喷管出口直径为50 mm，喷管面积比为1.25；在图1（c）中，收敛扩张喷管喉部直径为32 mm，喷管收敛段和扩张段角度分别为45°和15°。

在初始时刻，爆震管内完全填充静止的化学恰当比的氢氧混合物，喷管内填充静止的不可爆物质。由靠近封闭端的高温高压区直接起爆。高温高压点火区宽度为1 mm，压力和温度分别为200 kPa和3000 K。其它区域的初始压力和温度分别为100 kPa和293 K。爆震管左端推力壁为无黏绝热固体壁面。出口边界条件由出口流动情况确定，当出口流动为超声速和声速时，采用超声速出口边界；当出口流动为亚声速时，采用亚声速出口边界。环境压力和温度分别为100 kPa和293 K。

4 流场特性和性能分析

4.1 基准构型PDRE计算结果

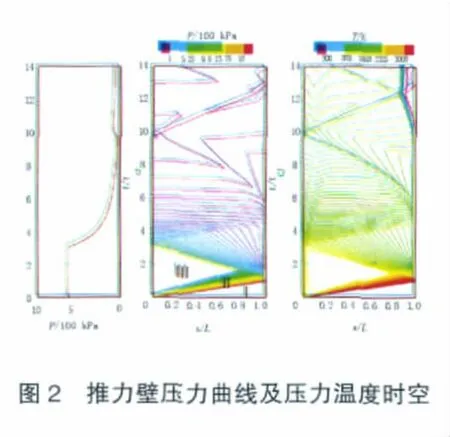
基准构型PDRE单次爆震过程的推力壁压力曲线及压力温度时空如图2所示，其中压力温度时空图的横、纵坐标分别被无量纲化。L表示爆震管长度（200 mm），tCJ等于爆震管长度除以CJ爆震波速。在图2中，Ⅰ区为爆震波前未受扰动的可爆混合物，Ⅱ区为Taylor膨胀波区，Ⅲ区为Taylor膨胀波波尾与推力壁之间的均匀区。爆震波以恒定速度向敞口端传播。从0时刻到爆震波到达敞口端的时间（爆震波传播时间）为0.0715 ms。爆震波到达爆震管敞口端后，在外界空气中形成透射激波，同时产生向爆震管内传播的反射特征膨胀波。反射特征膨胀波与Taylor膨胀波相互作用形成非简单区。可见，在排气过程中，流动受到多种波影响，流动情况比较复杂。

在单次爆震过程中，爆震管推力壁和出口压力曲线如图3所示。从爆震波形成直到第1道反射特征波到达封闭端前，封闭端的压力一直维持1个均匀值不变，呈现为推力壁压力平台区。随着第1道反射特征膨胀波的到达，更多的反射特征膨胀波到达封闭端，推力壁压力开始逐渐减小；,在压力减小过程中，会出现短时间的过度膨胀，推力壁压力略低于外界环境压力。随着排气过程的进一步进行，推力壁压力最终趋同于外界环境压力。爆震波达到爆震管敞口端前，爆震管出口压力等于可爆混合物初始填充压力；当爆震波到达敞口端，出口压力迅速增大；随着爆震波和爆震波后高压气体的逐渐排出，出口压力迅速减小。此外，在单次爆震排气过程中，虽然推力壁压力的压力已经减小至接近外界环境压力的水平，但是推力壁处的温度仍然较高，整个爆震管内的气体温度也较高。

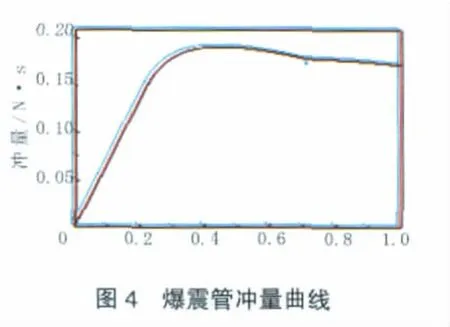
基准构型PDRE的冲量随时间变化曲线如图4所示。从0时刻（点火时刻）开始，爆震管推力壁压力高于外界环境压力，并产生推力，PDRE所产生的冲量逐渐增大。随着排气过程的不断进行，推力壁压力逐渐减小，冲量增大趋势变得较为平缓。当推力壁附近出现过度膨胀时，推力壁压力开始略低于外界环境压力，PDRE产生的瞬时推力为负，冲量略微减小。在0.4463 ms时刻，PDRE产生的冲量达到最大值0.19223 N·s。在1 ms内，基准构型PDRE的冲量及以可爆混合物为基础的质量比冲分别为0.172101 N·s和130.436 s。在相同的可爆混合物以及相同的初始条件下，采用热力学循环分析和性能计算[11]得到的理想爆震循环比冲为182.63 s。因此,基准构型PDRE单次爆震过程的质量比冲低于热力学计算值，这主要是由于爆震波后的高温高压燃气的内能并未完全转化为排气动能产生的推力。可以考虑在爆震管后安装排气喷管，来充分利用高温高压燃气的内能，以提高PDRE推进性能。

计算PDRE冲量（推力）的方法一般有进、出口平面动量平衡法和壁面压力积分法[11]。进、出口平面动量平衡法是取整个PDRE内的流体为控制体，根据动量守恒推导出PDRE瞬时推力的计算公式。对于单次爆震排气过程，如果利用爆震管出口流动来确定排气过程所产生的冲量，计算时间必须足够长，才能够消除非稳态效应的影响。因此,采用壁面压力积分法来计算PDRE瞬时推力。对于均匀直管构型的PDRE，可以通过推力壁压力积分得到其冲量。但对于非均匀直管构型的PDRE（如直爆震管后带有非等截面直管构型的排气喷管），推力壁压力积分结果不能反映整个发动机的推进性能，而需要对发动机所有固体壁面进行积分。

4.2 收敛喷管PDRE计算结果

带收敛喷管PDRE单次爆震过程的推力壁压力曲线及压力温度时空如图5所示。在爆震波到达喷管入口前，其流动情况与直爆震管的完全相同。爆震波到达可爆混合物与不可爆震物质的界面时，向爆震管上游反射膨胀波。当透射激波与喷管收敛段相互作用后，向上游反射压缩波，但并不是所有收敛段都首先反射出压缩波。收敛段首先反射膨胀波还是压缩波，取决于可爆混合物与不可爆震物质的界面位置、收敛段收敛角度等因素。反射的膨胀波和压缩波与爆震波后的Taylor膨胀波相互作用，形成更为复杂的波系。当膨胀波和压缩波到达推力壁后，推力壁压力有1个迅速减小并恢复的过程。随着更多的膨胀波逐渐传播到推力壁，推力壁压力开始逐渐降低。带有收敛喷管的PDRE推力壁压力降低至环境压力的时间约为基准构型PDRE的1.651倍。

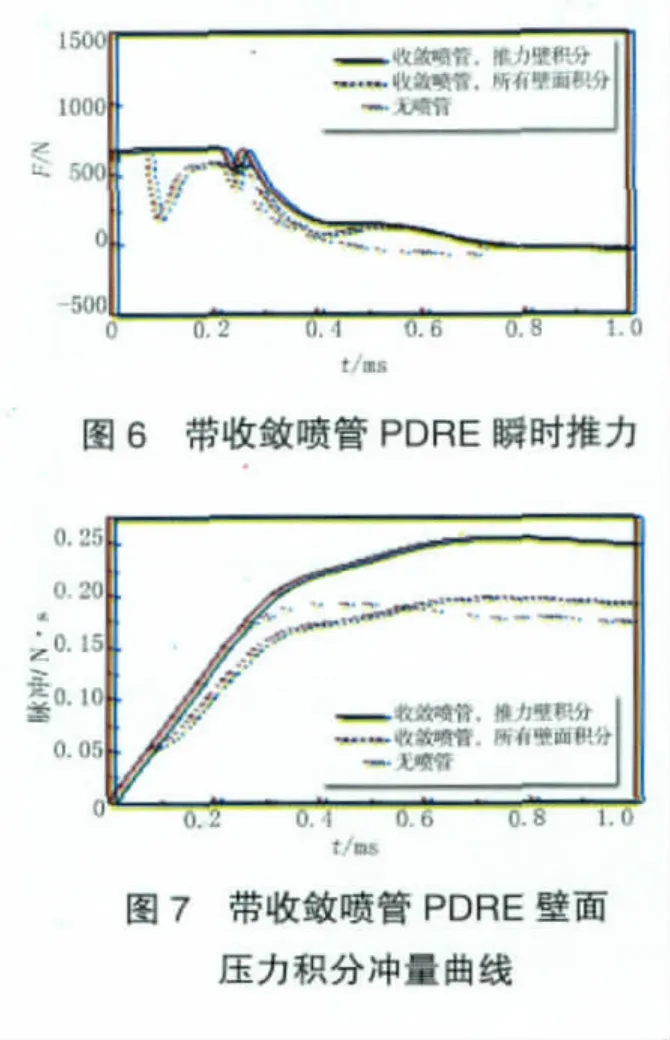
带收敛喷管PDRE的瞬时推力和壁面压力积分冲量曲线分别如图6、7所示。由图中可知，以推力壁压力积分和所用壁面压力积分得到的瞬时推力曲线存在较大差别。在爆震波到达喷管入口前，瞬时推力保持不变；当爆震波进入喷管，爆震波转化为激波，高压气体与喷管收敛段壁面作用产生负推力，使得整个PDRE推力迅速减小，随着气体排出，推力逐渐增大，并维持在一定水平基本不变。期间，推力的小幅减小并回升是由推力壁压力变化所引起的；随着排气过程进行，推力开始逐渐减小。在0.72665 ms时刻，带收敛喷管PDRE冲量达到最大值0.1972 N·s；在1 ms内，PDRE的冲量和比冲分别为0.190274 N·s和144.205 s。在相同积分时间内，带收敛喷管PDRE所产生的冲量比基准构型产生的冲量提高10.556%；但这一比冲值仍低于理想爆震循环的比冲（182.63 s），可以通过进一步优化排气喷管来提高。

4.3 扩张喷管PDRE计算结果

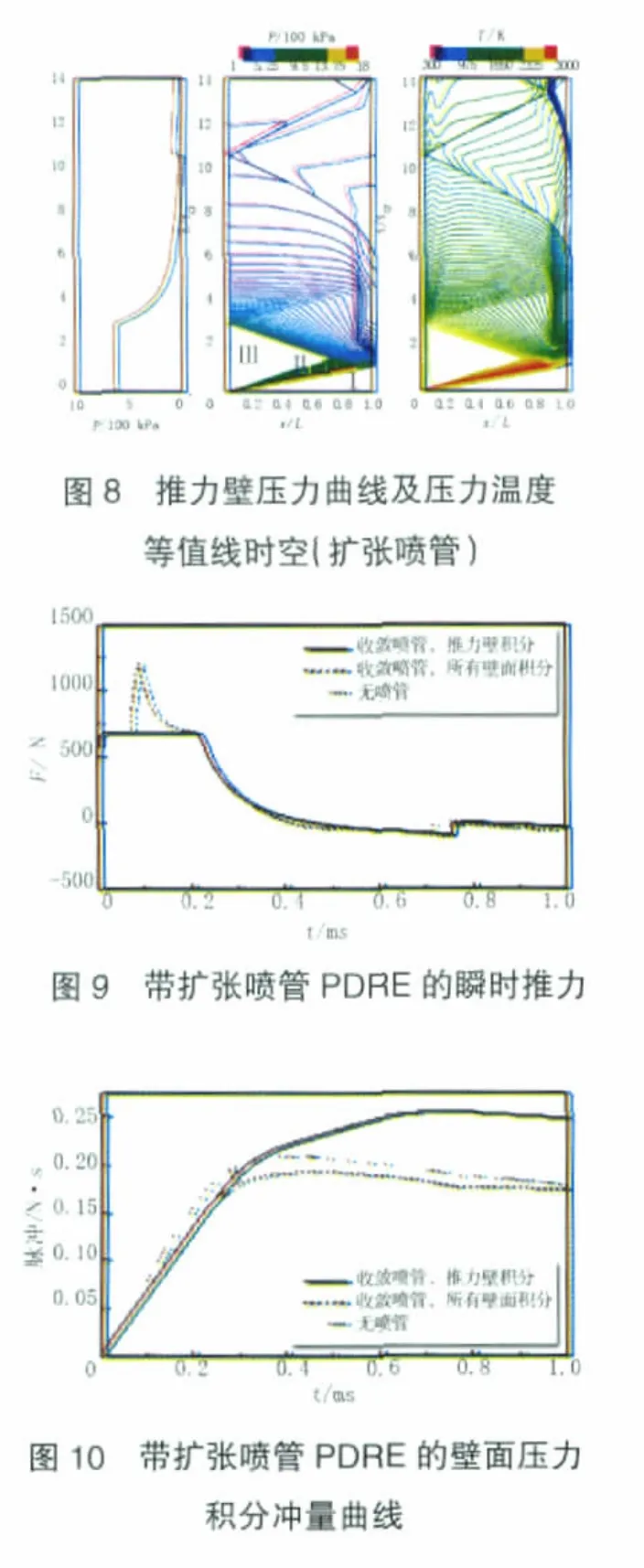
带扩张喷管PDRE单次爆震过程的推力壁压力曲线及压力温度时空如图8所示。带扩张喷管PDRE的推力壁压力曲线与基准构型PDRE的推力壁压力曲线基本相同。带扩张喷管PDRE的瞬时推力和壁面压力积分冲量曲线分别如图9、10所示。爆震波进入喷管后转化为激波，在高压气体与喷管扩张段壁面作用下，整个爆震管的推力迅速增大。随着排气过程的进行，推力逐渐减小；在排气过程后期，扩张喷管中的气流过度膨胀。在0.4035 ms时刻，带扩张喷管PDRE的冲量达到最大值0.20968 N·s；在1 ms内，PDRE的冲量和比冲分别为0.177661 N·s和134.646 s，比基准构型的提高了3.227%。

4.4 收敛扩张喷管PDRE计算结果

带收敛扩张喷管PDRE单次爆震过程的推力壁压力曲线及压力温度时空图如图11所示。

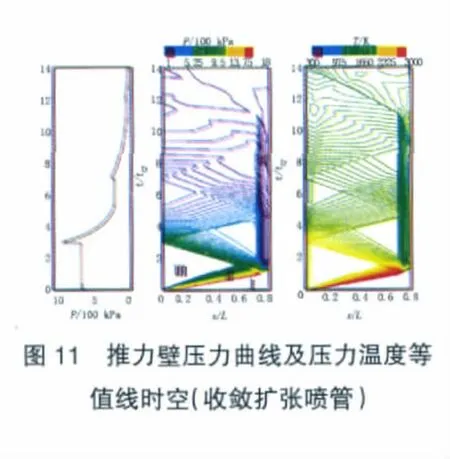
从图中可以看出，除了存在与基准构型PDRE压力温度时空图中相似的Taylor膨胀波区（Ⅱ区）和均匀区（Ⅲ区）外，收敛扩张喷管内还存在非常复杂的非定常波系（Ⅳ区）。在爆震波到达收敛扩张喷管入口前，其流动情况与不带喷管的直爆震管流动完全相同。当爆震波与喷管收敛段相互作用后，从喷管收敛段向上游反射压缩波；反射的压缩波与爆震波后的Taylor膨胀波相互作用，形成更为复杂的波系；当压缩波到达推力壁后，推力壁压力有1个迅速增大的过程。随着从喷管出口反射的膨胀波的逐渐传播到推力壁，推力壁压力开始减小，减小至环境压力的时间约为基准构型的1.544倍。收敛扩张喷管的存在，使得带收敛扩张喷管PDRE的排气过程较基准构型的更为复杂。

带收敛扩张喷管PDRE的瞬时推力和壁面压力积分冲量曲线分别如图12、13所示。在爆震波到达喷管入口前，瞬时推力保持不变；当爆震波进入喷管转化为激波后，在高压气体与喷管收敛段壁面作用下产生负推力，使得整个发动机的瞬时推力急剧减小。随着高压气体进入喷管扩张段，爆震管推力迅速增大，并维持在一定水平基本不变。PDRE的推力在呈现1个迅速增大的行程后，随着排气过程的继续进行，开始逐渐减小。在0.636ms时刻，带收敛扩张喷管PDRE的冲量达到最大值0.19334 N·s；在1 ms内，PDRE的冲量和比冲分别为0.18032N·s和136.661 s，比基准构型的提高4.772%。4种构型PDRE单次爆震的推进性能见表1。

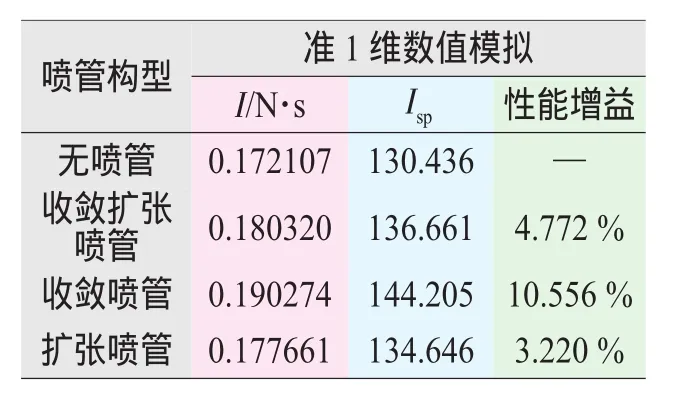
表1 4种构型PDRE推进性能比较

5 结论

通过对带喷管和不带喷管PDRE单次爆震排气过程的数值仿真可知，在爆震管完全填充的条件下，各种构型的喷管都能产生性能增益。喷管收敛段的存在，使得带收敛扩张喷管和收敛喷管PDRE的内部流场比不带喷管PDRE和带扩张喷管PDRE的更为复杂，推力壁压力松弛时间更长。带收敛喷管PDRE的性能增益最大，达到10.556%，但其值仍远低于理想爆震循环的比冲，可以通过进一步优化排气喷管来提高比冲。由于在排气过程的后期，扩张段内的气流过度膨胀会造成发动机性能损失，带收敛扩张喷管和扩张喷管PDRE的性能增益不如带收敛喷管的。可见,PDRE的喷管设计准则与常规稳态发动机的存在明显差异。

[1] Bussing T,Pappas G.An Introduction to Pulse Detonation Engines[C].AIAA paper 94-0263.In 32nd Aerospace Sciences Meeting and Exhibit,Reno,NV,1994.

[2] Kailasanath K.Recent Developments in the Research on Pulse Detonation Engines[J].AIAA Journal,2003,41(2):145-159.

[3] Roy G D,Frolov S M,Borisov A A,et al.Pulse Detonation Propulsion:Challenges,Current Status,and Future Perspective[J].Progress in Energy and Combustion Science,2004,30:545-672.

[4] Kailasanath K.A Review of Research on Pulse Detonation Engine Nozzles[C].AIAA paper 2001-3932.In 37th AIAA/ASME/SAE/ASEE Joint Propulsion Conference&Exhibit,Salt Lake City,Utah,2001.

[5] Strange G.On the construction and comparison of difference schemes[J].SIAM Journal of Numerical Analysis,1968（5）:506-517.

[6] Liou M S,Steffen C J.A New Flux Splitting Scheme[J].Journal of Computational Physics,1993,107(1):23-39.

[7] Liou M S,Edwards J R.Numerical Speed of Sound and its Application to Schemes for all Speeds[C].AIAA Paper 99-3268,In 14th Computational Fluid Dynamics Conference,Norfolk,VA,1999.

[8] Shu C W,Osher S.Efficient Implementation of Essentially Non-Oscillatory Shock-Capturing[J].Journal of Computational Physics,1988,77(2):429-471.

[9] Gamezo V N,Desbordes D,Oran E S.Formation and Evolution of Two-dimensional Cellular Detonations[J].Combustion and Flame,1999,116:154-165.

[10] Gamezo V N,Desbordes D,Oran E S.Two-dimensional Reactive Flow dynamics in Cellular Detonation Waves[J].Shock Waves,1999,9(1):11-17.

[11] 严传俊,范玮.脉冲爆震发动机原理和关键技术[M].西安：西北工业大学出版社,2005,122-198.