复合材料层压结构铺层顺序优化设计特征提取算法

罗鹏，马力，孙爱军

（1.沈阳发动机设计研究所，沈阳110015；2.海军驻沈阳地区发动机专业军事代表室，沈阳110043；3.海军驻平坝地区航空军事代表室，贵阳561102）

1 引言

与传统金属材料相比，复合材料具有可设计性强、比模量和比强度高、抗疲劳、耐腐蚀性能好等优点，已经在很多军、民工业领域取代前者，获得广泛应用[1]。由单向带铺叠而成的层压板结构是复合材料的1种重要应用形式。而复合材料层压板铺层顺序决定了层压板的弯曲、屈曲及振动特性[1]，是复合材料层压结构设计的基础和关键技术。为了充分发挥复合材料的可设计性，许多研究者采用了诸如遗传算法[2]、蚁群算法[3]、模拟退火算法[4]、粒子群算法[5]等现代优化技术，对层压板的铺层角度顺序和层数进行优化，取得了一定效果。简单、高效的优化方法一直是工程优化设计研究的有效手段。

本文提出1种“特征提取”的优化算法，并以文献算例来检验算法的性能。

2 特征提取算法

2.1 随机化优化流程

与传统优化法相比，遗传算法、蚁群算法、模拟退火算法、粒子群算法等采用了随机化技术的现代优化方法，具有可处理离散变量的组合优化、无需目标函数导数信息、不要求目标函数有显式表达式、鲁棒性强和易于编程等优点。这些采用了随机化技术的优化算法的基本流程如图1所示，其中，编码操作可以看作对设计变量空间进行变换fcode(·)；解码操作为其逆变换(·)；更新种群操作可看作基于排序后的上代搜索状态点的转移变换fupdate(·)。算法之间的主要区别在于算法提出的启发模型不同，进而转换函数fcode(·)·)和fupdate(·)的具体表现形式有所不同。由于转换函数的具体形式会影响到优化算法的效率和稳定性，人们开展了很多致力于转换和改进转换函数具体形式的研究[2,6]，但又囿于具体算法原始启发模型的限制，对复合材料层压结构优化问题本身的特征关注不够，导致函数转换的具体形式过于复杂，也限制了算法性能的提高。

2.2 特征提取算法提出和实现

借鉴随机化优化的通用流程，受感知和认识过程的启发，结合复合材料层压结构优化问题的特点，对通用流程中的编/解码、群组更新环节进行有别于遗传算法、蚁群算法等现有算法的改造，使群组更新过程成为对群组内的占优群体进行“特征提取”的过程。

从感知和认识的过程来看，认识主体首先抓住的或者有深刻印象的是认识对象的主要特征，此时获取的关于对象的信息包含了一定的“背景噪声”，以突出主要特征；随着感知过程的完成和认识的深入，对“背景噪声”的逐步过滤，完善对象细节特征的认识。另外，由复合材料层压板基本理论可知：在确定的材料体系下，各角度铺层比例和铺层顺序决定了层压板的力学性能[1]。可以推想：各角度铺层比例和铺层顺序都相近的铺层方案，性能表现也相近；而丢失任何1个确定问题的最优方案的特征，都会导致性能下降，丢失越多，下降越大。换句话说，保留了更多最优方案的特征的方案更接近于最优方案；在1组随机产生的方案中，表现较优的那些方案必定共同和更大程度地包含了最优方案的特征。基于这些认识和设想，提出称为“特征提取”的搜索状态转移函数的实现步骤，如下所述：

（1）Do from j=1 to j=m;(m为群组规模)。

（2）随机生成“特征提取”指示向量Pj=(p1,j,p2,j…pi,j,…,pn,j)。其中，pi,j(i=1,2,…,n)为取值范围，是1≤pi,j≤λm的自然数，指示排序序号，可以按均匀分布随机产生，也可以按非均匀分布随机产生，使靠前的序号占优；λ为小于1的正数，根据实际情况，λ可取0.1至0.5之间的数；

（4）随机生成“背景噪声”向量S=(s1,s2,…，si…,sn)，控制噪声水平使之不掩盖特征提取，即随机数si的绝对值取值范围远小于设计变量xi的取值范围。

（6）End do。

在“特征提取”的更新操作过程中，各分量里出现频次较高、对应目标函数值较优的取值作为“特征”会被“提取”，并保留；“特征”不突出的分量的取值会逐渐被“噪声”掩盖。在整个优化搜索过程中，“特征”不断地被突出和提取，“噪声”逐渐被过滤。

复合材料层压板中铺层角度的变化主导着层压板性能的变化，角度改变越小，性能改变也越小；好的优化算法对铺层角度变量的编码和解码也应考虑这一特点。在铺层坐标系中，-45°与135°等价，鉴于此，当铺层角度取离散值0°、45°、-45°、90°时，采用135°替代-45°，进而编码转换函数fcode(·)设为fcode(θ)=θ/45，即编码后的角度变量x取值为：0、1、2、3。对任一角度变量编码x进行更新操作后，增加1步x=mod(x,4)的操作，便可保证角度变量编码x各取值之间的“距离”大小与对应角度值之间的“距离”大小是相关的。例如：与编码值0临近的是1和3（3=mod(-1,4)），对应的与0°临近的角度是45°和135°（即-45°）。

3 算例

基于前述思想，编写了复合材料层压结构优化程序，并结合文献算例进行了验证。

例1：16层4边简支层合板的铺层优化，使屈曲载荷系数最大[2,6]。层压板的长a=0.508 m，宽b=0.254m，每层厚度t=0.0127 cm。承受的x方向均布轴压Nx=175 N/m和y方向均布轴压Ny=KNx，其模型如图2所示。材料常数为：E1=128 GPa，E2=13.0 GPa，G12=6.4 GPa，v12=0.3，ρ=1.6×103kg/m3。

采用商用有限元分析软件Ansys（采用shell 99号单元，整个模型划分为18×36=648个单元）进行数值计算，首先利用文献[2]的数值计算结果校验临界屈曲载荷系数计算精度。表1列出了文献[2]的结果和本文模型的验算值，可知相对误差较小。

采用本文提出的方法，设置种群规模为20收敛条件为连续4代出现的最优值相等，最大迭代次数为20。所得到的载荷比K各种取值下的最优方案及相应的临界屈曲系数见表2。

由表2可知：采用此方法，在各种载荷比K下，都能够搜索到不差于文献[2]的最优解，并且，当载荷比K=2.000、K=2.450时，得到的铺层方案对应的临界屈曲系数略高于文献[2]的结果。其中，当K=2.000时，本文结果与文献[2]结果的铺层比例相同，而靠近中面处的铺层顺序不同；而当K=2.450时，本文结果的铺层比例便与文献[2]的结果不同，相应的临界屈曲系数高于文献[2]的，与文献[6]的结果一致。

（1）在载荷比K=0.125、K=0.150和K=0.240的情况下，均得到各角度铺层比例相同、+45层和－45层位置恰好对换的2种铺层方案。考虑到结构形状和载荷的对称性，2种铺层方案实质上是相同的。

（2）相比于文献[2]的结果，增加计算了载荷比K=1.000、K=3.000这2种情况。由各种载荷比情况下的最优铺层方案及相应的临界屈曲系数值可以看出：在各种情况下，最优铺层方案中均不含0°铺层；随着载荷比K值的增大，45°铺层的比例逐渐下降，而90°铺层的比例逐渐上升。K值较小（K=0.125），即x方向（长度方向）的载荷占主导时，对应最大临界屈曲系数的最优铺层全为+45°和-45°铺层；K值较大（K=3.000），即y方向（宽度方向）的载荷占主导时，对应最大临界屈曲系数的最优铺层全为90°铺层。

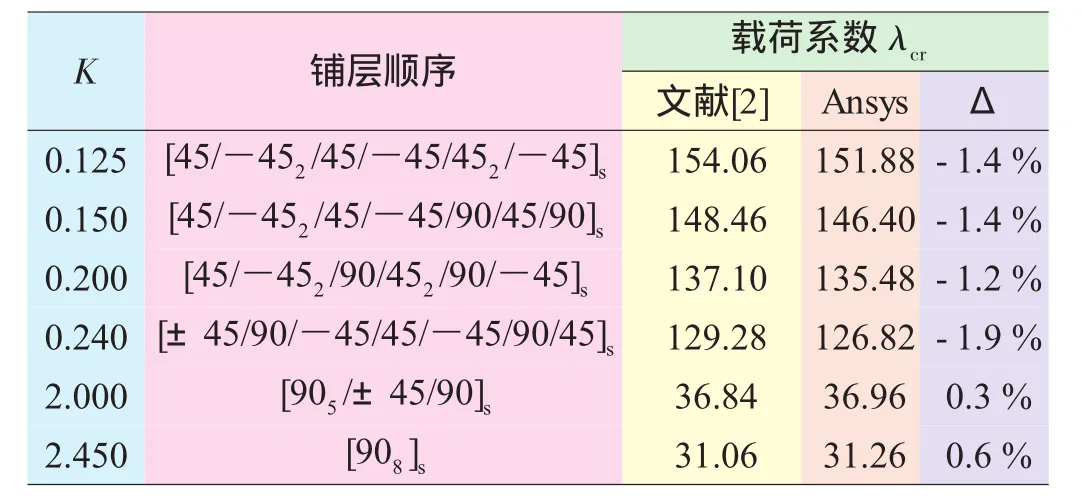
表1 文献[1]中不同载荷比下最优方案的屈曲系数计算值与Ansys计算值比较

表2 采用本文方法在不同K值下的最优方案及相应的临界屈曲载荷系数

例2：复合材料层合圆柱壳的铺层优化[6]。长度为40 cm、平均半径为10 cm的复合材料层压圆柱壳，1端固支，1端自由，优化目标为使其1阶自然频率最大化。材料参数同例1的。采用Ansys对该结构进行分析，其有限元模型由800个4边形shell 99单元组成。采用本文的有限元模型对文献[6]的方案进行验算的结果见表3，可知计算结果的相对误差很小；本文模型合理，可以作为优化设计中的分析模型。

表3 文献[6]中最优方案的1阶自然频率计算值与Ansys计算值比较

采用本文的优化程序得到使1阶自然频率最大的方案有2种，分别为：[0/45/－45/905]s和[0/－45/45/905]s，互为镜像；相应的1阶自然频率为：503.155 Hz。优于文献[6]给出的方案值。目标函数（1阶自然频率）的收敛曲线如图3所示，本文方法在10代内便收敛，并且得到更优的解，算法效率较高。

4 结束语

与遗传、蚁群、模拟退火等算法相比，本文算法的群组更新过程无需根据目标函数进行复杂的适应值或转移概率的计算和确定，更为简练。数值算例表明，本文提出的优化算法是有效的，相关设想也是合理的；对于复合材料层压结构铺层顺序优化这类离散变量优化问题，以本文方法能够得到满意的结果，在2个算例中均有优于文献结果的表现。还具有编程简单、效率较高的特点，便于解决其它的工程优化问题。

[1] 沈观林,胡更开.复合材料力学[M].北京：清华大学出版社,2006．

[2] Haftka R T,Walsh J L．Stacking-sequence Optimization for Buckling of Laminate Plates by Integer Programming[J]．AIAA J,1992,30(3)：814-819．

[3] Aymerich F,Serra M.Optimization of Laminate Stacking Sequence for Maximum Buckling Load Using the Ant Colony Optimization(ACO)Metaheuristic[J].Composites:Part A,2008,39:262-272.

[4] Ozgur Erdal,Sonmez Fazil O.Optimum Design of Composite Laminates for Maximum Buckling Load Capacity Using Simulated Annealing[J].Composite Structures,2005,71:45-52.

[5] Omkar S N,Dheevatsa Mudigere,et al Vector Evaluated Particle Swarm Optimization(VEPSO)for Multi-objective Design Optimization of Composite Structures[J].Composite Structures,2008,86:1-16.

[6] 唐文艳,顾元宪,赵国忠.复合材料层合板铺层顺序优化遗传算法[J].大连理工大学学报，2004，44(2)：186-189.