超空泡高速航行体动力学建模与控制设计
王京华,张嘉钟,于开平,魏英杰,黄文虎,吕 瑞
(哈尔滨工业大学航天学院,哈尔滨150001,wangjh1920@163.com)
因为超空泡在水下减阻的应用前景,已经有大量的数值模拟和实验来研究超空泡形成、发展和稳定的机理和规律[1-2],目前已经取得一定进展.在对空泡机理有了一定了解的基础上,开展了超空泡航行体动力学建模与控制方面的研究[3-7],文献[3]在空化器瞬时速度方向决定空泡外形的基础上分析了超空泡航行体的流体动力,建立了二维非线性动力学模型,使用了精确线性化方法设计控制器;文献[4]在航行体尾部滑行力计算过程中考虑了空泡的记忆效应,使用预测控制实现避障跟踪;文献[5]建立的模型和文献[3]相似,研究了超空泡航行体的非线性动力学问题;文献[6]在建模的过程中在某个平衡点附近采用小扰动线性化方法建模,之后使用线性鲁棒控制方法;文献[7]用滑模控制和LPV研究了超空泡航行体的控制.
本文为了对超空泡航行体进行动力学建模,基于空泡膨胀独立性原理研究了空泡的记忆效应及其对空泡形态的影响,又考虑了空化器定向效应和空泡尾部上飘变形,在分析空泡形态的基础上计算了空化器和尾翼流体动力以及尾部滑行力,还得到了尾翼效率变化规律计算公式.设计了极点配置和预测控制方法来进行深度跟踪,提出了一种避免滑行力出现的策略,避免滑行力可以有效减少摩擦阻力,减少航行体与空泡壁碰撞产生的冲击,增加系统的稳定性,对于超空泡航行体在未来的实际应用具有重要意义.
1 超空泡航行体动力学建模
1.1 空泡形状计算
准确地获得超空泡的形状是计算航行体各部分水动力的基础.根据Logvinovich创立的空泡膨胀独立性原理[7],超空泡的整个运动过程可以看成是空泡的各个横截面按照一定规律的独立膨胀过程,各个截面的膨胀情况只与空化器经过该截面的时刻的空化数、速度等状态有关,而与航行体在其它时刻的运动无关.空泡的这种特点就像是对过去有记忆功能一样,称为空泡记忆效应.假设t时刻空化器中心的深度为z(t),t-τ时刻空化器中心的深度为z(t-τ),用空泡中心线的上漂尺寸h1和空化器定向效应引起的变形h2进行修正,那么在t时刻的空泡中心线上在t-τ时刻空化器经过点的截面处的深度为z(t-τ)+h1+h2.
Logvinovich[8]在势流理论分析和试验的基础上,给出了超空泡形状的半理论半经验公式,后人的大量实验和数值模拟都验证了该公式的正确性[9],该文献中的空泡半径计算公式和空泡半径收缩速度公式具体计算见文献[8].
在重力场中由于受到浮力作用空泡会逐渐上漂[8],空泡中心轴线的上漂和空泡的上漂幅值是近似相等的,越到空泡后部上漂越显著,在小空化数下,与空化器距离为x处的空泡上漂尺寸为

其中:ζ=x/Lk,Lk为空泡半长,文献[8]中给出了Lk的计算公式.
空化器攻角引起的空泡变形称为空化器的定向效应[8],小空化数下与空化器距离为x处的空泡偏移尺寸为

其中:Fy等于空化器升力大小Fcav,Fcav的计算将在1.2节给出,计算时也应考虑记忆效应,将结果代入式(1)得

其中τ为空化器运动距离x所需的时间.
1.2 流体动力计算
根据文献[3]建立的体坐标系,原点位于航行体头部的圆盘形空化器顶端面的圆心,x轴与航行体对称轴重合指向前,z轴垂直于x轴指向下.z轴方向的速度是w,V代表纵平面内航行体头部空化器的合速度,θ是航行体俯仰角,q是体坐标系下的俯仰角速度,航行体深度为z.在w较小时有dθ/dt=q,dz/dt=w-Vθ.
空化器的作用除了用来产生和维持超空泡外,还作为一个控制面控制航行体头部的流体动力,空化器在纵平面内旋转形成的攻角变化可以提供不同的升力,作用于空化器上流体动力的升力分量为[8]

其中:cx是圆盘形空化器与来流垂直时的阻力系数,cx=cx0(1+σ),cx0=0.82,αc=w/V+δc,δc是空化器偏转角度;ρ为水的密度.尾翼也需要提供一定的流体动力来产生控制力矩,在一定空化数下,通过设计使空泡中心线与航行体中心点重合时尾翼浸入水中的长度是全长的一半,参考文献[3]的方法,尾翼流体动力为

其中:

式中:δf是尾翼偏转角,n是尾翼效率.
尾翼只有浸入水中的部分与水直接接触才能发挥控制面的作用,这里将尾翼浸入水中的长度与全长的比值称为尾翼的效率.在实际航行过程中,由于航行体与空泡位置关系的相对变化,尾翼的效率也是不断改变的.航行体尾部垂直截面处空泡中心线的深度为z(t-τ)+h1+h2,航行体尾部截面中心的深度为z+Lθ,这两个深度的距离为

通过几何关系可以计算出尾翼效率为

当航行体中心和空泡中心偏离程度过大,尾翼可能全部浸入水中时,翼效率为1,这时满足条件

尾部滑行力对于超空泡航行体的整个运动过程分析是很重要的,当滑行力产生时,航行体尾部和空泡内壁的相互作用过程可以当作细长体浸入液体考虑[10],当航行体尾部的一部分浸入到水中时,设h为浸入深度,α是浸入角度,这种情况下使用浸入曲线边界液体的圆弧物体问题的解,计算公式如下:
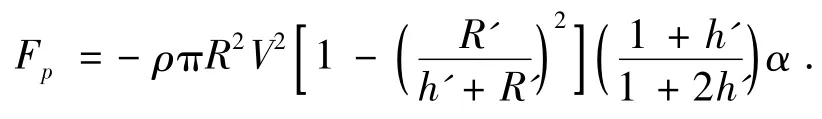
其中:R'=(Rc-R)/Rc,h'=h/R,根据运动过程中航行体与空泡的位置关系可以算出h和α.

1.3 非线性动力学模型
根据文献[3-5]中的假设,航行过程中推力和阻力保持平衡.假设巡航速度V的大小保持不变,根据动量、动量距定理和上文流体动力的计算结果可以得到非线性动力学方程为

其中:
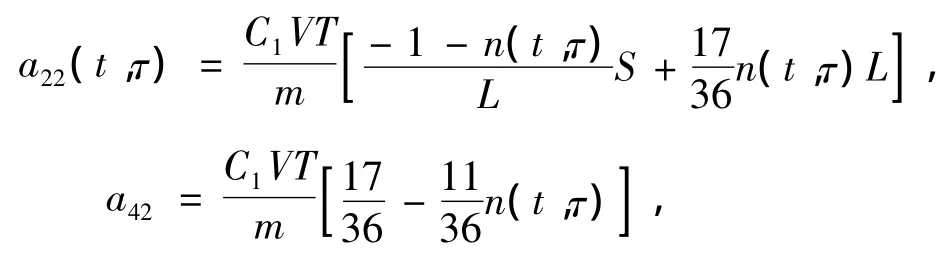

2 极点配置控制设计
超空泡航行体的模型式(4)可表示为非线性仿射形式

取输出为

对于此非线性MIMO系统采用输入/输出间的精确线性化方法[11],通过计算知模型具有相对阶向量(r1,r2)=(2,2),并且系统的相对阶向量有定义,总相对阶为4,这时不必考虑内动态的稳定性,输出变量与输入的关系为

通过反馈

实现了输入/输出间的精确线性化,而且还实现了输入/输出的解耦.得到输入/输出的动态方程为

这时采用鲁棒极点配置方法来设计控制器.
航行体结构参数等按照文献[3]选取,零初始状态下跟踪5 m的深度,得到仿真结果如图1所示,航行体深度z较快地达到跟踪深度,跟踪效果较好,出现了一段时间的滑行力,但是在控制作用下逐渐过渡到无滑行力状态,这时空化器和尾翼共同作用来平衡航行体的重力.前0.5 s内几乎一直存在的滑行力,会增加航行体的阻力,航行体与空泡壁接触也会造成冲击.不足之处是控制输入δf过大.
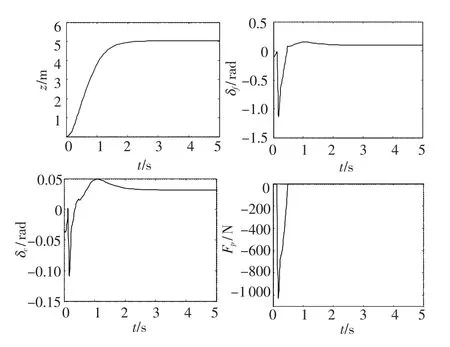
图1 极点配置控制
3 预测控制设计
航行体尾部与空泡壁接触时会产生滑行力,滑行力的出现会增加航行体的摩擦阻力,并且高速航行过程中突然出现的滑行力会给航行体造成振动与冲击,因此,如果能有效避免滑行,可以减少能量消耗,并减少航行体与空泡壁碰撞产生的冲击,增加系统的稳定性.控制滑行力的可行办法是把与滑行力相关的量作为一个输出变量,并约束该变量的取值范围.另外,控制输入空化器和尾翼的偏转角要满足一定的约束条件.若输出变量和输入变量都满足一定的物理约束,,则预测控制最显其优势[12],下面推导预测模型.由于能避免滑行力是非常有益的,假设通过适当的控制可以不产生滑行力,那么超空泡航行体的动力学模型式(4)可表示为

通过反馈线性化将重力影响产生的C项消去后得到

离散化得

取采样周期T为0.008 s,根据文献[3]的参数,在空化器处形成的超空泡到航行体尾部会有0.024 s的延迟时间,借鉴文献[4]的方法取新的状态变量为

新的状态方程为

由式(2)可知滑行力的出现与空泡中心线和航行体中心的距离有关,输出的第8个变量用来表示这个距离,输出方程为

其中:C'=[1 0 L0 0 0 -1].预测控制问题描述为[12]

对于有约束控制可以转化为二次规划问题进行求解.
如果要避免滑行力的产生,就要控制航行体尾部横截面处航行体中心和空泡中心的距离,使航行体无法接触到空泡壁,在文献[3]的航行体结构和空化数等条件下航行体尾部边缘和空泡壁间隙为3.94 cm,为了保证空泡出现扰动情况下设计方法仍然有效,约束航行体尾部横截面处航行体中心和空泡中心距离不超过3 cm.约束控制输入空化器和尾翼偏转角大小分别在0.2 rad和0.5 rad以内;限制纵向速度 w大小不超过10 m/s;为了满足小角度假设,俯仰角大小不超过0.08 rad;为了使航行体在空泡内摆动的速度不过大,因此限制俯仰角速度大小在1 rad/s以内.
零初始状态下跟踪5 m的深度,仿真结果如图2所示,有效地避免了滑行力的出现,这点也可以从航行体中心线和空泡中心线之间的距离看出来,与有滑行力状态相比,可以减少摩擦阻力;控制输入饱和问题也得到了解决,控制面偏转角被限制在要求的范围内.
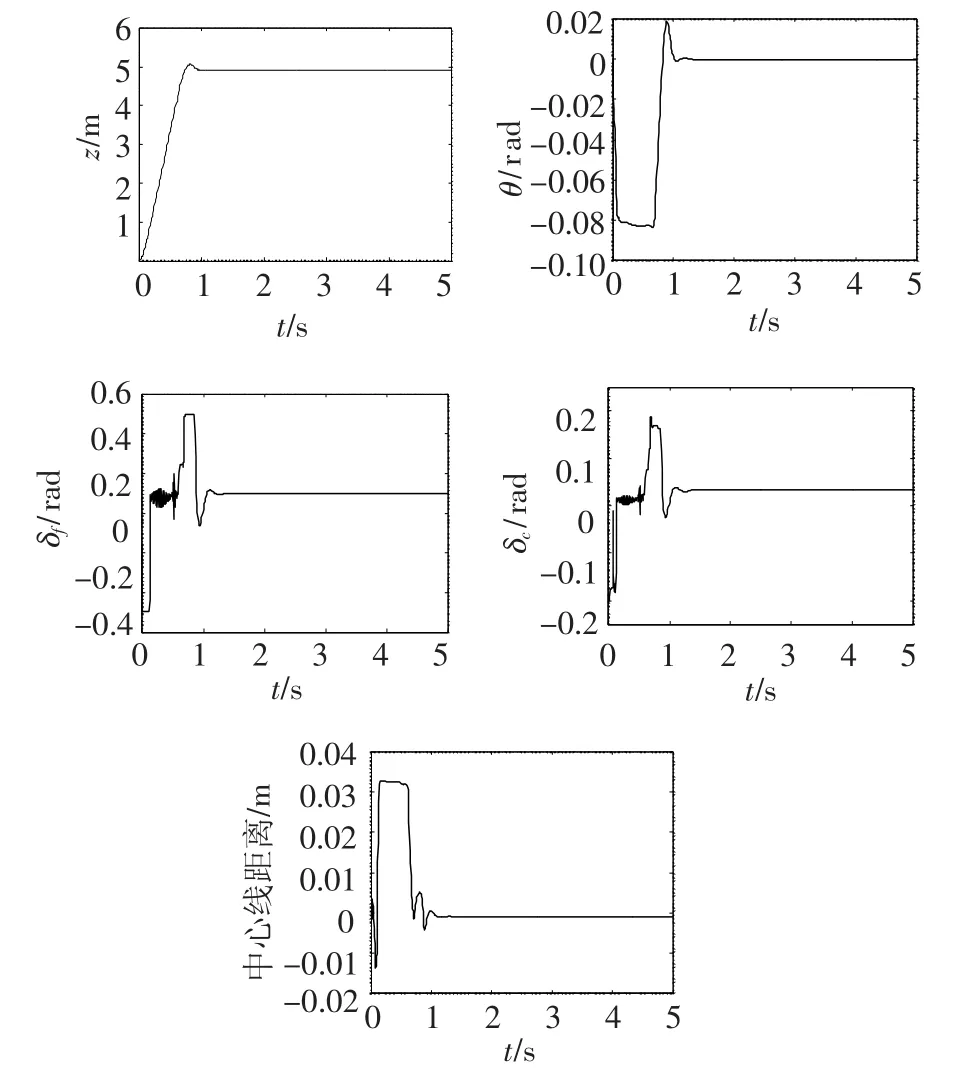
图2 预测控制
4 结论
文中根据文献[8]提出的空泡膨胀独立性原理,考虑了空泡的记忆效应等对空泡外形和流体动力的影响,详细计算了超空泡航行体各部分所受的流体动力,研究了航行过程中尾翼效率变化计算方法,建立了超空泡航行体非线性动力学模型.基于输入输出精确线性化的极点配置控制器深度跟踪效果较好,但是容易出现调节器饱和,滑行力较大;为了解决极点配置的不足,设计了预测控制方法,提出了航行过程中避免滑行力出现的策略来减少摩擦阻力和增加系统的稳定性,仿真结果表明设计的预测控制方法可以成功地在航行过程中避免滑行力.
[1]SAVCHEKO Y N.Supercavitation-problems and perspectives[C]//Fourth International Symposium on Cavitation.California:California Institute of Technology,2001:1-8.
[2]曹伟,魏英杰,王聪,等.超空泡技术现状、问题与应用[J].力学进展,2006,36(4):571-579.
[3]DZIELSKI J,KUDILA A.A benchmark control problem for supercavitating vehicles and an initial investigation of solutions[J].Journal of Vibration and Control,2003,12:791-804.
[4]VANEK B,BOKOR J,BALAS G J,et al.Longitudinal motion control of a high-speed supercavitation vehicle[J].Journal of Vibration and Control,2007,13:159 -184.
[5]LIN Guojian,BALACHANDRAN B,ABED E H.Dynamics and control of supercavitating vehicles[J]. Journal of dynamic systems,measurement,and control,2008,130(02):021003.1-021003.11.
[6]GOEL A.Robust control of supercavitating vehicles in the presence of dynamic and uncertain cavity[D]. Florida:University of Florida,2005:47-58.
[7]MAO Xiaofeng,WANG Qian.Nonlinear control design for a supercavitating vehicle[J].IEEE Transactions on control systems technology,2009,17(4):816-832.
[8]LOGVINOVICH G V.Hydrodynamics of flows with free boundaries[M].Kiev:Naukova Dumka,1969.
[9]于开平,蒋增辉.超空泡形状计算及相关试验研究[J].飞航导弹,2005,12:15-22.
[10]LOGVINOVICH G V.Some problems of planning[J]. Transaction ofCenterAerohydrodynamicsInstitute,1980,2:2052.
[11]KHALIL H K.非线性系统[M].第三版.朱义胜,董辉,李作洲,等,译.北京:电子工业出版社,2005.
[12]丁宝苍.预测控制的理论和方法[M].北京:机械工业出版社,2008.

