神经网络应用于大坝安全评价的方法研究

王玉成

（江苏省电力设计院，江苏南京211102）

0 引言

大坝安全评价是一个非常复杂的过程，其过程实际上可以理解为：y=f（x1，x2，……，xn），其中y为大坝安全度，x1，x2，……，xn为影响大坝安全的各种因素，例如变形、裂缝、渗流等。传统的大坝评价方法往往是富有经验的专家依据工程实际情况、历史经验、物理力学关系等，给出合理恰当的评价，一旦有新情况就需要重新做出判断。而神经网络模型可以通过对历史样本的自主学习，在输出的评价结果中再现专家的思维和经验，得出比较合理的评价结论，节省大量人力物力。

传统大坝安全评价方法是对变形、渗流、应力分别建立统计模型，然后对监测资料进行回归分析，不能为神经网络模型提供合适的学习样本，因此提出一种新的大坝安全评价方法，为神经网络应用于大坝安全评价提供可能。

1 大坝安全评价新方法

大坝安全评价是一个极其复杂的过程，各种因素相互影响，错综复杂。例如大坝结构安全由变形、渗流、应力等方面决定，而其中变形的安全又由径、切向水平位移和垂直位移的安全程度决定，径、切向水平位移的安全程度又由某些重点坝段的径、切向位移监测值的安全程度决定。因此，可行的方法是逐级而上，对某些重点坝段径、切向位移监测值的安全度进行评价，得到评价值，然后把它们对大坝整体径、切向水平位移安全程度的影响值（所占权重）剥离出来，两者结合考虑得到大坝整体径、切向水平位移的安全程度值。依此层层而上，最终得到整个大坝的安全程度值。图1为某大坝安全度评价结构示意图。

图1 某大坝安全度评价结构示意图Fig.1 Schematic drawing of safety evaluation for a dam

采用此种方法理论上可以进行大坝安全度评价，但是需要解决两个主要问题：如何对评价结构中处于底层位置的重点坝段径、切向位移观测值安全度进行评价；如何科学合理剥离出下一级因素对上一级因素安全值的影响程度（权重）。

1.1 安全度值评价

参考有关文献，将大坝安全指标等级定为5级（正常，基本正常，轻度异常，重度异常，恶性失常），将其用数轴上（0～1）区间内相对应的5段范围进行量化。

表1 大坝安全指标等级Table 1:Grades of dam safety indexes

大坝原位监测资料在参与大坝安全评价时可以从效应量的数值表现来考虑，主要是将实测值与模型拟合值及所建立的大坝安全监控指标来进行比较。监控指标是用来衡量大坝运行是否正常、安全的一种数值界限。当实测值在监控指标规定的范围以内或数值以下，一般认为大坝运行是正常的，否则就不安全。大坝安全监控指标可分为警戒值和危险值两类。警戒值是反映大坝正常与否的界限值，它主要根据观测量与荷载间的物理关系并结合以往测值的变化范围和规律来拟定。界限值是反映大坝安全与否的界限值，它主要根据安全要求所限定的效应量数值来确定。

设数学模型表示为：ŷ=f（x1，x2，……，xn），则监控指标一般可表示为：

式中，[y]为监测量y的监控指标界限；ŷ为监测量y的统计估计值；xi为影响监测量y的主要环境因素变量；ε为置信带宽，当采用监控模型法确定监控指标时，可取ε=pS，其中p=1～3，S为模型剩余标准差：

式中n为模型中实测效应量总数，k为实测效应量的自由度。

所以监控指标公式可表示成：

因此评价指标等级区间A区、B区、C区、D区、E区也可以用监控指标来划定，这样能使人为划定的等级区间和通过统计模型回归分析所得的监控指标相挂钩，使评价结果更合理，更具科学性。

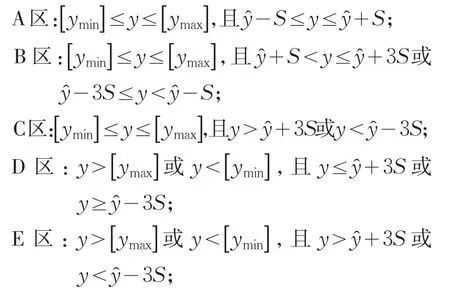
ymax,ymin为监控指标的限制值。

推导可得安全度值计算公式见表2。

表2 安全度值计算公式Table 2:Formulas for dam safety calculation

这样，评价指标等级区间A区、B区、C区、D区、E区和监控指标相联系，使人为划定的等级区间和通过统计模型回归分析所得的监控指标相挂钩，解决了大坝安全评价结构最底层因子的安全度评价问题。

1.2 权值分析

在得到大坝安全评价结构最底层因子的安全度评价度值后，如果能确定底层因子相对于上一层因子安全度所占的权重，就能确定上层因子的安全度。本文提出用主成分分析法和层次分析法相结合的方法来确定下层因子的权重。

1.2.1 主成分分析法（PCA）

根据主成分理论，主成分分析直接依据原始实测资料的信息，通过正交变换，把多个相关指标转化为少量不相关评价指标，并定量描述交互指标在整体系统中贡献，并通过贡献量大小来识别对应的各个评价指标的权重值。

PCA的主要步骤是依据大坝监测资料建立监测资料相关矩阵，然后进行一系列的矩阵变换运算，最后得到权重矩阵（过程略）。

1.2.2 层次分析法（AHP）

层次分析法（Analytic Hierarchy Process，AHP）是系统工程中对非定量事件作定量分析的一种简便方法，它能实现大坝专家主观判断的客观描述。其主要步骤如下：

（1）确定评价目标A和评价因素集U。

（2）构造判断矩阵P。以A表示目标，ui表示评价因素，ui∈U(1，2，…，n)，uij表示ui对uj的相对重要性数值（也称为“标度”）(j=1，2，…，n)，则

P也称为A-U判断矩阵。

（3）权数分配。由A-U矩阵求出最大特征值所对应的单位特征向量。所求单位特征向量各分量即为各评价因素重要性排序，也即权数分配。

（4）检验。以上得到的单位特征向量即为所求权向量，为了检验权重的分配是否合理，需要对判断矩阵进行一致性检验，使用公式：

式中：CR——判断矩阵的随机一致性比率；

CI——判断矩阵的一般一致性指标，由公式CI=(λmax-n)/(n-1)计算；

RI——判断矩阵的平均随机一致性指标，对于1～9阶判断矩阵，RI的值列于表3。

表3 RI值表Table 3:RI values

当CR＜0.1时，即认为判断矩阵具有满意的一致性，说明权重系数分配合理，否则就需要调整判断矩阵，直到取得满意的一致性为止。

2 实例计算

为了验证本文提出方法的可行性，采用某大坝1999～2006年间的变形数据进行计算。

该大坝变形因子下属有径向水平位移因子、切向水平位移因子、垂直位移因子。根据该大坝本身坝体结构，参考专家意见，选择底层因子见表4。

表4 底层因子选择Table 4:Underlying factors selected

采用1999～2004年的数据进行建模分析，选取2005年1月17日、2月20日、2006年1月6日、2月4日当日的变形安全度值作为检验数据（篇幅原因，只选取少量进行说明）。

依照前文所述，先对底层因子进行建模分析，确定监控模型，然后进行安全度判断，再进行求权工作，层层而上，最后得到位于顶层的大坝整体变形安全度。

现仅将部分中间计算结果列出。

根据所建监控模型及大坝原位观测数据，根据表2计算得底层因子安全度值。

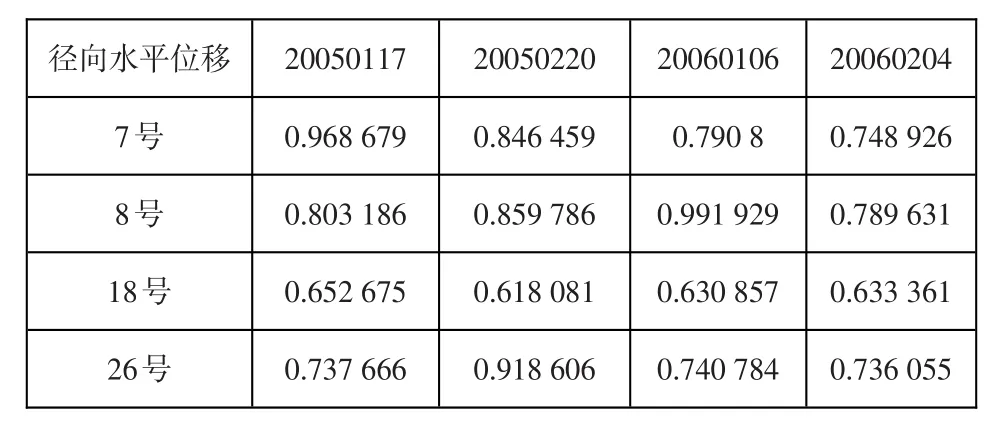
表5 径向水平位移下属因子安全度值Table 5:Safety values of subordinate factors of the radial hori⁃zontal displacement

依据大坝监测资料，建立监测资料相关矩阵进行主成分分析，可得底层因子相对于上层因子安全度的权重。

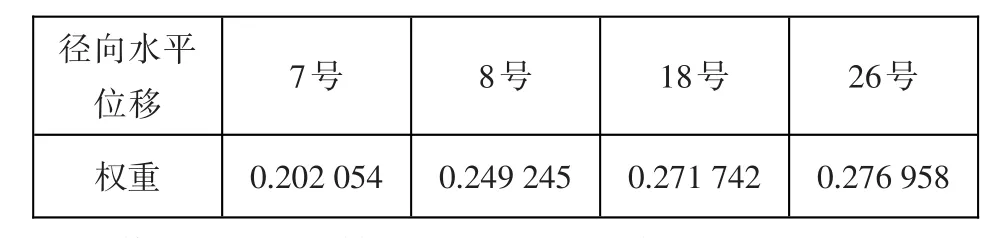
表6 径向水平位移下属因子权重Table 6:Weights of subordinate factors of the radial horizontal displacement

依据上述计算结果，两者综合考虑即可得径向水平位移因子安全度值。

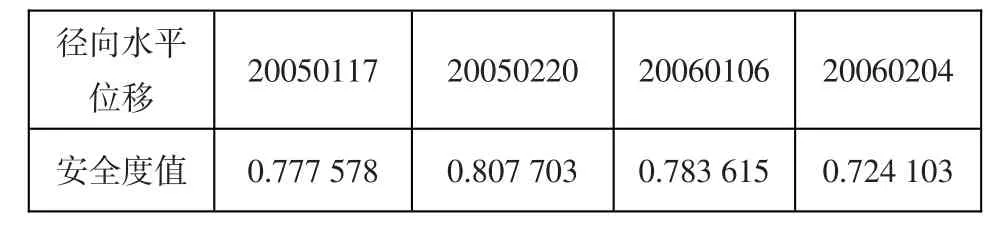
表7 径向水平位移因子安全度值Table 7:Safety values of the radial horizontal displacement factor

同理可得切向水平位移因子和垂直位移因子安全度值。

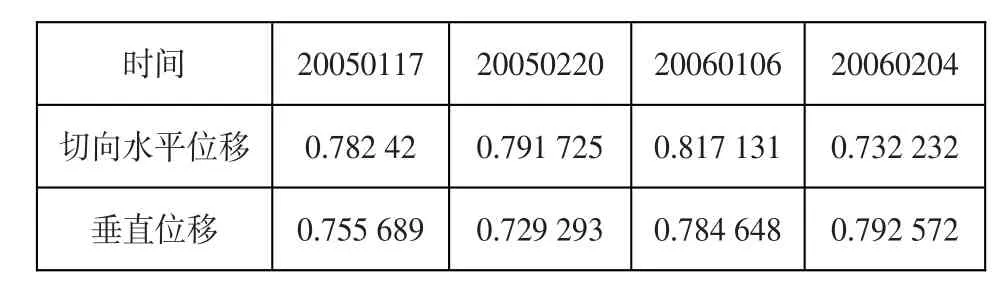
表8 切向水平位移因子及垂直位移因子安全度值Table 8:Safety values of the tangential horizontal displacement fac⁃tor and vertical displacement factor

在进行变形因子安全度求解时，径向水平位移和垂直位移采用不同的回归模型，回归参数不同，如果采用PCA法进行求权的话，很难选择数据，也不能保证结果的可靠性，因此采用层次分析法进行求权工作，结果见表9。

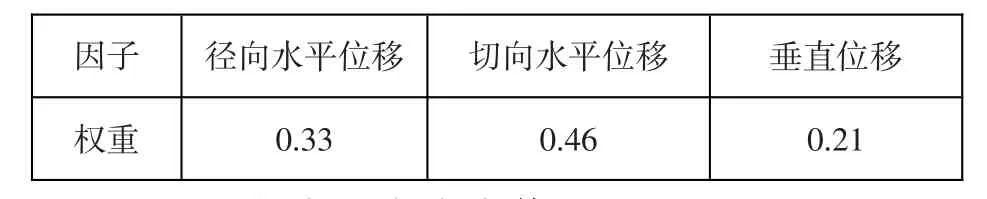
表9 径向水平位移因子、切向水平位移因子、垂直位移因子权值Table 9:Weights of radial horizontal displacement factor,tan⁃gential horizontal displacement factor and vertical displace⁃ment factor

最后可得变形安全度值。

表10 变形因子安全度值Table 10:Safety value of the deformation factors

该大坝已运行30余年，其工作状态基本正常，处于正常可控范围之内。从表10计算结果中可看出，大坝在2005、2006年1、2月份气温较低、水位较低的不利运行工况下，安全度值处于基本正常水平，与大坝实际监测结果相符，与传统分析方法结果相符，证明本文方法具有一定的可行性。

3 结语

神经网络方法应用于大坝安全评价具有其不可比拟的优势，但现有评价方法无法为其提供学习样本。本文提出了一种新的大坝安全评价方法，实现了传统安全度评价值的量化，以及从底层因子开始层层向上，最终判断大坝整体安全度的过程，为神经网络应用于大坝安全评价提供了可能。另外，在此基础上进行了实例计算，所得结果与常规方法所得结果相符，与实际情况相符，证明该方法具有一定的可行性，将神经网络应用于大坝安全度评价领域是可行的。■

[1]吴中如，沈长松，阮焕祥.水工建筑物安全监控理论及其应用[M].南京:河海大学出版社，1990.

[2]吴中如，朱伯芳.三峡水工建筑物安全监测与反馈设计[M].中国水利水电出版社，1999：81～104.

[3]汪培庄.模糊集合论及其应用[M].上海科学技术出版社，1983：201～224.

[4]黄健元.模糊集及其应用[M].宁夏人民教育出版社，1999：15～35.

[5]赵斌，吴中如.BP模型在大坝安全监测预报中的应用[J].大坝观测与土工测试，1999,23(6).

[6]杨杰，吴中如，顾冲时.大坝变形监测的BP网络模型和预报研究[J].西安理工大学学报，2001,17(l):25～29.