圆形坝下涵管结构内力与变位计算及抗裂验算解析法
蔡勇斌,刘女英,蔡勇平,蔡晓鸿
(1.江西省吉安市水利局,江西吉安343000;2.江西省吉安市水利水电规划设计院,江西吉安343000)
0 引言
坝下涵管是中小型水库工程常用输水建筑物,其结构设计首先应进行承载能力极限状态计算。此外,坝下涵管不允许出现裂缝,以免危害大坝安全,需满足抗裂要求[1]。
有必要指出,目前坝下涵管按独立构件进行分析计算,计算理论与模型均欠合理,拙文给出的坝下涵管结构内力与变位计算及抗裂验算解析法弥补了上述缺陷,具有实际应用意义。显然,所获成果可顺利应用于圆形隧道结构内力与变位计算。
1 弹性地基圆弧曲梁控制微分方程
坝下涵管承受竖向荷载qv、水平侧向荷载qH(θ)(qH1、qH2分别为涵管顶、底水平侧向荷载)、自重G和外水压力p0(θ)等主动荷载与土体弹性抗力被动荷载的作用(图1)。其最不利计算工况是涵管内无水检修期荷载组合。
坝下涵管弧段,可视作弹性地基圆弧曲梁。涵管结构、荷载关于CD直线对称。设圆心为坐标原点,管壁厚h=r1-r0;断面中心半径为ri=0.5(r0+r1),H为顶部水头,γω为水的重度,混凝土重度为γc、弹性模量为Ec,断面面积为F,惯性矩为I0。截取微分单元ridθ,其中径向位移为W(θ),切向位移为V(θ),K为涵管周边土体抗力系数,涵管与土体间的剪应力为τ,断面的弯矩为M(θ),剪力为Q(θ),轴力为N(θ),曲梁截面角位移为ϕ(θ)(图2)[2]。上述各力与夹角θ均以图示方向为正。

图1 圆形坝下涵管计算简图Fig.1 Schematic drawing for circular embedded pipe in calculation

图2 微分单元受力示意图Fig.2 Schematic drawing of forces in differentiation element
列出微段的静力平衡方程,略去二阶微量后有[2]

对式(6)从0到θ积分,并注意到
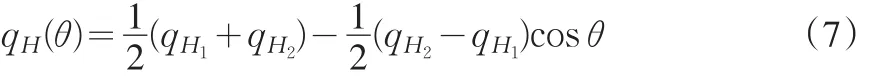
整理得
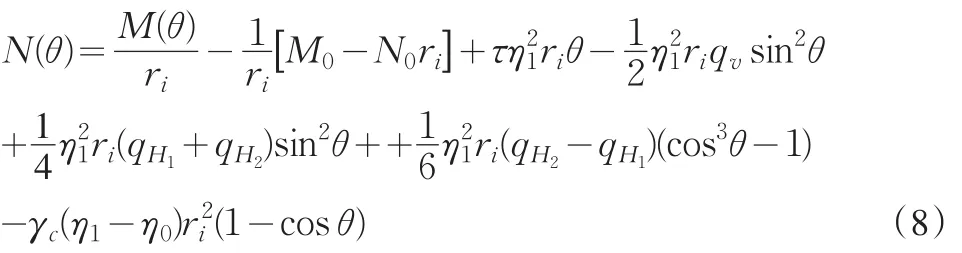
又由结构力学知,径向位移与截面内力间有关系式
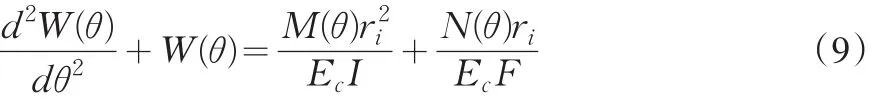
据式(4)~(9),可导出径向位移W(θ)应满足的控制微分方程
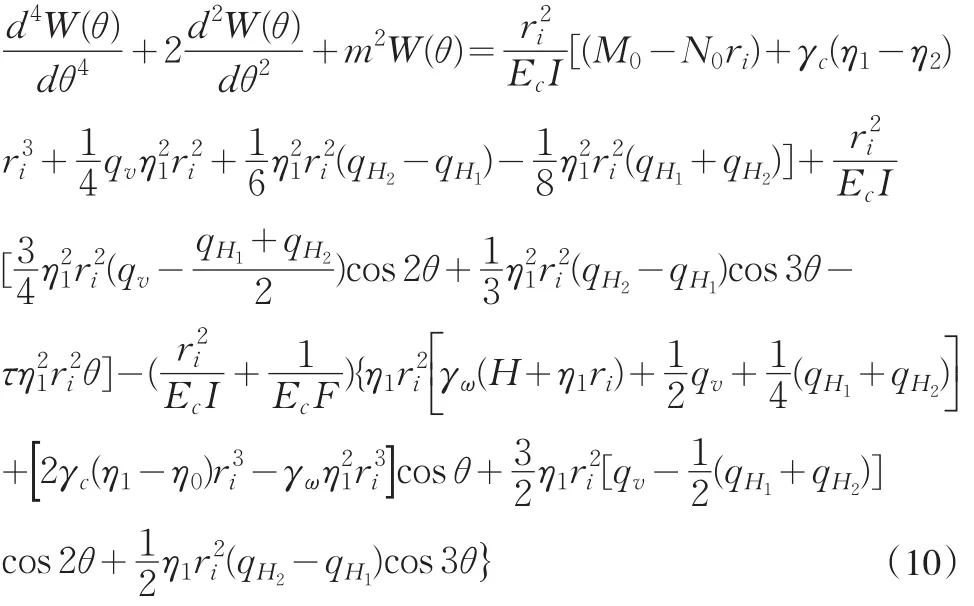
2 弹性地基圆弧曲梁内力与变位计算
微分方程式(10)的解由特解W0(θ)与基本解W1(θ)组成[3],即

其特解为
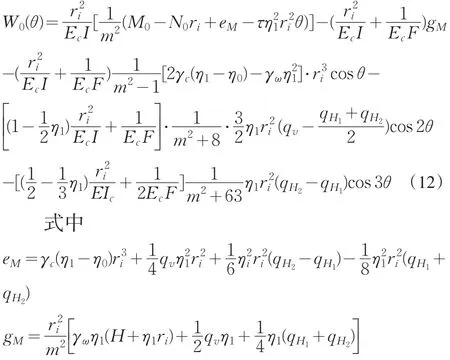
其基本解W1(θ)为

据式(11)、(12)、(13)可得弹性地基曲梁截面角位移
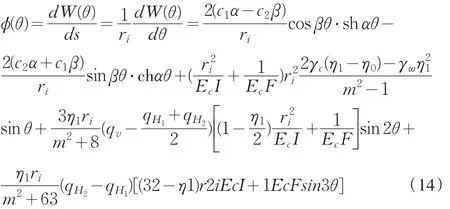
当坝下涵管未出现裂缝时,据对称性W(π)=W(-π),可得c1=c3,c2=-c4,τ=0;又由,得c1=0,c2=0。于是式(11)可改写成
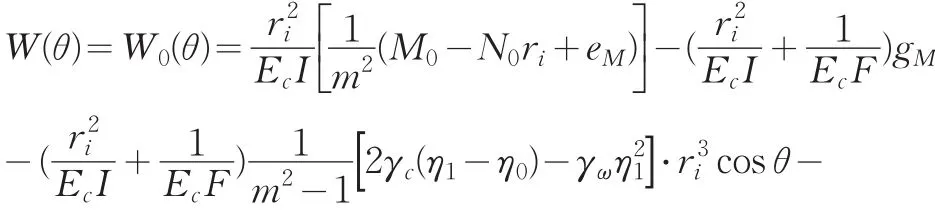

相应弹性地基曲梁内力与角位移ϕ(θ)表达式为

忽略轴向力产生的切向应变εθ,有切向位移[4]
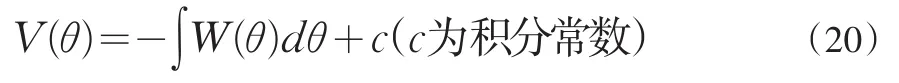
将式(15)代入上式积分,并利用V(θ)|θ=0=0确定微积分常数C,可得

3 坝下涵管结构内力与变位解析计算式及抗裂验算

将式(22)代入式(15)~(19)、式(21),可得圆形坝下涵管内力与变位解析计算式


坝下涵管在外压荷载作用下,内缘、外缘的切向应力σθ计算式为[2]
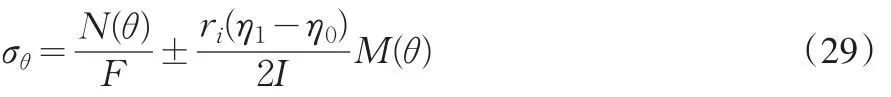
将式(16)、(17)代入上式,整理得

将求解式(31)、(32)所得θ值代入式(30),即可得到坝下涵管切向应力极大值,将其与混凝土轴心抗拉强度ftk进行比较,便可判定坝下涵管是否满足抗裂要求。
4 工程算例
钢筋混凝土圆管结构,r0=1.25 m,r1=1.45 m,Ec=2.535×107kPa,rc=24.53 kN/m3,γω=9.81 kN/m3,qv=333.43 kN/m,H=10 m,k=1.96×104kN/m3。于是有ri=1.35 m,η1=1.074074074,η0=0.925925925,F=0.2 m2,I=6.666666667×10-4m4,m2=5.1451,α=0.7963,β=1.2783。
计算bM、cM、dM、gM、fM值,据式(26)~(28)可得圆管内力计算式,将所计算点位的角度值代入,可得圆管各点内力值如表1所示。

表1 圆管结构内力计算结果表Table 1:Calculation result of the structure inner force of the cir⁃cular embedded pipe
利用式(23)~(25)可计算出圆管各点变位值;利用式(30)计算参数B、C、D、E值,代入式(31)、(32),可求算出圆管切向应力极大值相应点位的角度值;再将所得极值点的角度θ值代入式(30),即可得出切向应力极大值σθmax,进而将其与混凝土轴心抗拉强度ftk相比较,便可判别圆管是否出现裂缝,具体计算不予赘述。
5 结语
圆形坝下涵管与圆形隧道目前多采用数值计算方法对其进行内力近似分析。本文采用坝下涵管(隧道)结构与岩土体联合工作模型[5,6],通过建立弹性圆弧曲梁控制微分方程,给出了圆形坝下涵管(隧道)结构内力、变位及抗裂验算计算方法与相应解析计算式,揭示了相关物理力学参数对结构内力、变位的影响,且可用于数值计算方法精度的定量评估。■
[1]SL191-2008,水工混凝土结构设计规范[S].北京:中国水利水电出版社,2009:9~14.
[2]蔡晓鸿,蔡勇平.水工压力隧洞结构应力计算[M].北京:中国水利水电出版社,2004:224~232.
[3]卢存恕.建筑结构中的应用数学[M].北京:中国建筑工业出版社,1987:45~51.
[4]王维英.用伽辽金权残法分析圆形隧道[J].水利学报,1990,(1):49~54.
[5]蔡勇斌,蔡勇平,吴韶华.坝下埋管环向裂缝与轴向抗裂验算[J].大坝与安全,2008,(4):1~3.
[6]张志坚,项和祖.石门水库输水管的加固设计[J].大坝与安全,2005,(1):73~75.

