多分类支持向量方法的本科招生生源质量模型

邢 涛，廖 冉

(1.北京航空航天大学经济管理学院，北京100191，xt@buaa.edu.cn; 2.北京航空航天大学数学与系统科学学院，北京100191)

近年来，高等教育已从“精英教育”快速向“大众化教育”转变，高校招生规模逐年扩大，使得高校在生源上竞争日趋激烈.怎样从全国的高考生中录取更多的优质生源，成为各高校招生工作者的一大难题.各高校招生工作部门一直在积极探索一套科学、有效、完善的招生管理和评价体系［1］.在现行招生制度下，高考成绩仍然是绝对性指标.随着高校招生改革的推进，高考自行命题省份不断增加，高考也从最初的全国统一标准变得更具区域性特色.因此，如何在兼顾教育公平的原则下，合理安排招生计划，从而在全国众多的报考学生中科学、公正、高效地挑选出有发展潜力的优秀学生是提高生源质量的关键问题.以往的高校本科招生生源分析，并未充分挖掘高校历年已录取的学生信息.教育的发展具有持续性，一个地区以往的生源质量往往能够反映出该地区的教育水平，从而指导今后的招生工作，而高校本身拥有的庞大的学生信息资源也恰好利于这一方法的实施.

统计学习理论是专门研究有限样本情形下的机器学习规律的理论，在这一理论基础上发展出了一种通用学习算法，相比起传统统计方法所采用的经验风险最小化原理，支持向量机算法采用了结构风险最小化理论并体现出了优于传统统计方法的一些性能［2］.多分类支持向量机算法是传统支持向量机算法的推广，该算法不仅继承了支持向量机算法稳健且计算精确等特点，而且克服了传统支持向量机算法只能解决二分类问题的局限.

本文利用多分类支持向量机算法，根据各地区学生在大学期间的学习成绩，与学生入学前的信息特点，探讨本科生源质量预测体系，建立本科生源质量分析模型，为高校制定招生计划、提高生源质量提供有效的参考信息.该模型可以对高校的招生工作给出初步的参考.

1 支持向量机

支持向量机算法是建立在统计学习理论的结构风险最小化原理基础上的，能较好地解决小样本问题，同时具有很好的泛化能力.算法由Vapnik等［3］在1995年左右提出.近些年来，该算法在实际应用及理论推导中都有着长足的进步.韩媚和郭丹凤［4］将支持向量机方法应用到了高校就业情况的分析中.向小东和宋芳［5］利用基于核主成分分析的支持向量机算法对福建省的失业率进行了有效的预测和分析.相比其他传统的统计学分类方法或是带有学习过程的人工智能算法，如神经网络方法，支持向量机算法能够克服过学习问题和维数灾难问题，具有全局最优的特点和很好的泛化能力［3］.该算法主要有以下两个特点［6］:

(1)采用结构风险最小化原则，所得到的学习机器有着很好的泛化能力，即由有限的训练样本得到的小误差能够保证对独立的测试集仍保持小的误差.

(2)支持向量机算法最终将转化为一个凸优化问题，局部最优解一定是全局最优解.

支持向量机算法的基本思想是在样本空间或者特征空间，构造出最优超平面，尽可能将不同类的数据点分开，并使得超平面与不同类数据点之间的距离最大，从而达到最大的泛化能力.在线性可分情况下，如图1所示，圆圈和方块分别代表两类样本点，每类中处在边界的点为支持向量，这些支持向量所形成的超平面H1和H2为能撑起不同类别样本点的分类超平面，其之间的间隔为类与类之间的最大间隔，因此最佳的分类面H0介于这两个分类超平面之间.

图1 线性可分下的支持向量机模型

假设样本集合为S={(xi，yi)∈Rn×{±1}，i=1，…，m}，其中x为输入样本，y为输出样本.用x∈A，y=1表示一类点，x∈B，y=-1表示另外一类点.算法的目标是利用训练样本提供的信息来估计一个分类器，即函数f:Rn→{±1}.如果训练样本是线性可分的，那么必然存在(w，b)∈Rn×R使得wTx+b=0为其线性边界，且满足wTx+b≥1(x∈A)和wTx+b≤-1(x∈B).该限制条件可被表示为:yi［(wT·xi)+b-1］≥0，得到决策函数:fw，b(x)=sign(wTx+b)，其中w为权重向量，b为偏离值.最终该问题可以转化成为求解如下二次优化问题:

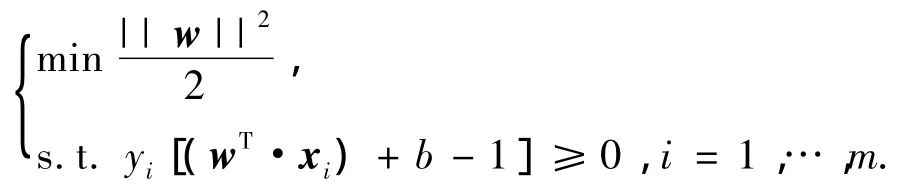
然而，在实际问题中常常遇到线性不可分的情形，支持向量机算法的优势也体现在其能处理非线性复杂系统中的问题，它能通过非线性变换将该非线性问题转化成为某个高维空间中的线性问题，在高维空间中求取最优分类面实现线性分类.这种非线性变换是通过定义适当的核函数实现的，在本文中特别应用到了希尔伯特再生核空间HK

［7］中的两种常用的核函数，其定义如下:

高斯核函数:

多项式核函数:

2 多分类支持向量机

支持向量机的产生最初是为了解决二分类问题，但在实际应用中，往往要求算法可以对多于两类的分类问题给出准确的判断.因此，随着实际应用的广泛要求和理论研究的深入，多分类支持向量机算法就此产生.

多分类支持向量机算法在很多领域中都有着广泛的应用，Yoonkyung Lee等［8］应用多分类支持向量方法对基因表达谱数据和卫星放射数据进行了分析.Dirong Chen等［9］对多分类支持向量机算法的收敛性给出了理论分析.窦智宙等［10］应用该方法对彩色癌症细胞的图像进行了分割.康文雄等［11］应用小波分解和多分类支持向量机算法处理了脸谱识别问题.

2.1 多分类问题及贝叶斯决策

在多分类问题中，考虑如下样本(xi，yi)，i= 1，…，m.，其中，xi∈Rd为输入样本，yi∈{1，2，…，k}为输出，代表了输入样本的分类情况.主要目标是找到一种分类法则，使得分类法则φ(x)可以尽可能精准的刻画输入xi和输出yi之间的关系.假设样本为独立采样且满足分布P(x，y)，pj(x)=P(Y=j|X=x)表示样本x被分到第j类的概率，当各类别之间的错分误差相等时，分类法则φ(x)的损失可由如下函数定义:

其中:I(·)为势函数，若自变量为真，则取值为1，为假则取值为0.此时，最佳的分类法则为贝叶斯分类，即

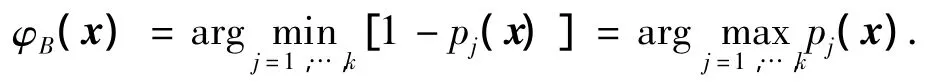
当错分误差不一样时，定义矩阵C，Cjl表示第j被错分到l的惩罚.显然有Cjj=0，j=1，2，…，k，此时

通过最小化风险函数得到的最优分类器为

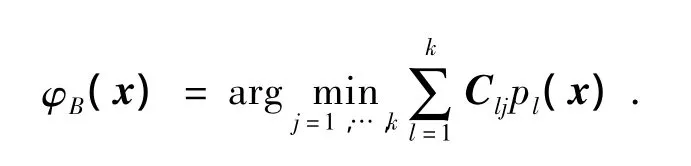
但在实际问题中，往往需要定义不同的错分惩罚，遇到这样的情况可以通过调整矩阵C中的元素值来表示不同的错分误差.

2.2 一对一(one against one)多分类支持向量机的数学模型

传统的SVM算法是专门处理小样本问题的，因此在考虑多分类问题时可以将问题转化成为多个二分类问题，这样的多分类支持向量机算法称为一对一的多分类算法［12］.

一对一分类是在k类训练样本中构造所有可能的两类分类器，每个分类器仅仅在k类中的两类训练样本上训练，结果共构造k(k-1)/2个分类器，测试样本经过各个分类进行分类，每次将样本判为某一类，最终得到判入次数最多的类为样本的最后结果.但这种算法的运算量大，计算步骤很多，相应的运算时间也会长.

2.3 一对多(one against all)多分类支持向量机的数学模型

一对多方式的主要思想是构造k个二分类器，每个二分类器应用于所有样本，第i个二分类器将样本分为第i类和其他类，这k个二分类器组合起来就可以形成N分类的判决函数.当一个样本数据输入时，依次用这k个二分类器进行判断，如果第i个二分类器的输出是属于第i类，而其他的分类器都输出为其他类，则判断该样本属于第i类.

多分类支持向量机算法最终转化为求解如下优化问题:

其中:向量vi∈Rk记录分类结果，如果样本xi属于第j类，则向量vi第j个元素为1，其他元素为-(k-1)-1;且映射L(yi)第j个元素为0，其他元素为1的向量，满足限定条件)=0.该问题的最优解的算法求解过程本文借助libsvm工具包［13］中SVMtrain函数完成.

3 高校生源质量分析模型

基于多分类支持向量机的生源质量分析模型由数据采集、数据预处理、特征指标选取、数值归一化和学习过程组成，如图2所示.

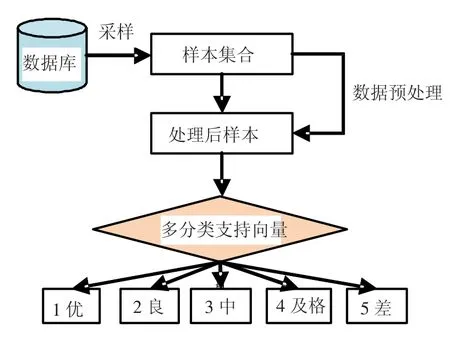
图2 多分类支持向量机模型

1)数据采集器.按用户要求从数据库中采集数据;

2)数据预处理.剔除残缺数据和奇异数据，如各省份特招生的样本.由于各个省份的录取标准不同，分数之间的差距也很大，所以对高考成绩进行层次化处理，共分为11档次，如表1所示.

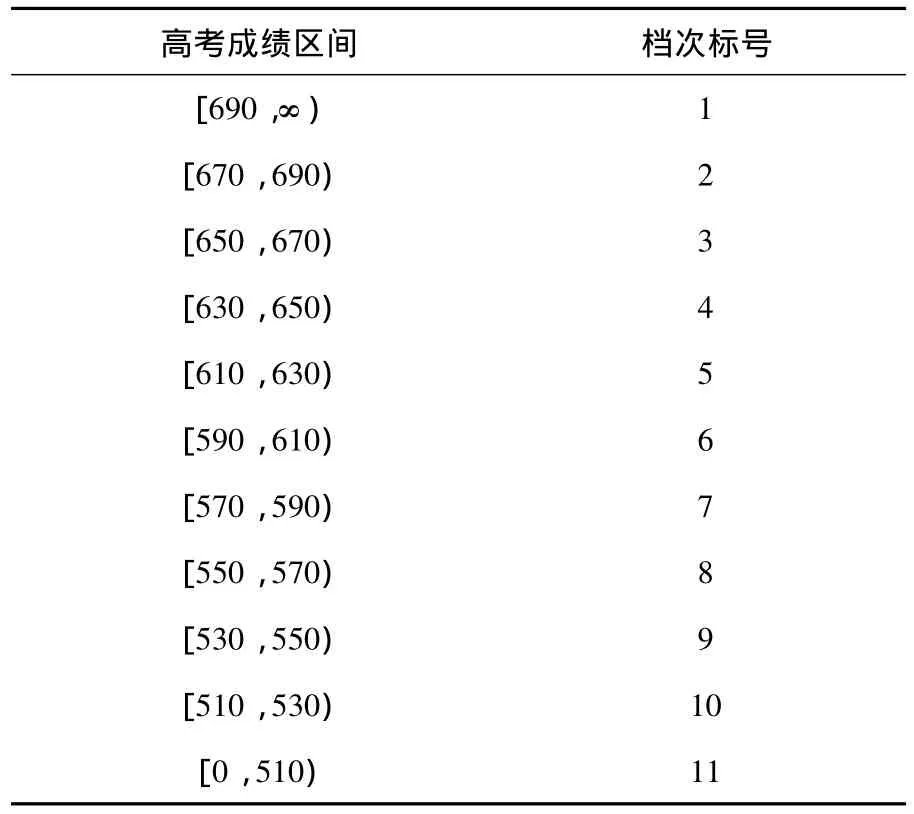
表1 高考成绩分层处理

3)特征指标选取.从学生信息库中依照数据的属性和对问题的贡献选取了省份、高考成绩、所在省份排名、毕业时所在专业排名情况这4个指标组成了样本的有效信息(见表2).

表2 有效样本

4)数值归一化处理.由于各个指标之间数值的差别很大，所以对数值进行归一化处理，使得数值分布在［-1，1］之间:

5)训练及学习过程.对有标号的样本，根据其毕业时所在专业的排名进行分类(见表3):

表3 带标号样本的分类情况

4 测试实例与分析

数据来源主要是某大学某年级3 000余名本科学生的数据.其中包括学生入学时的高考成绩以及在高中时期的其他信息(包括是否是三好学生、优秀学生干部，是否在学科竞赛中获奖等)，另外一部分信息如生源所在省，录取时所在省份的排名情况以及高考成绩.研究的数据量足够大，具有普遍性，使分析结果具有一定说服力.

4.1 多分类支持向量机模型的分类情况

实验基于高斯核函数及多项式核函数展开，并选取了不同核宽及不同的阶数进行了对比，在表4中，MSVM表示多分类支持向量机模型，RBF-1表示核宽为1的高斯核，POLY-1表示阶数为1的多项式核.在实验过程中，采用10倍交叉验证方法(10-fold cross validation)测试各个模型的分类结果，即将数据集分成10组，轮流将其中9组做训练，1组做测试，10次的结果的均值作为对算法精度的估计，结果分别呈现了均值和波动值.

为比较多分类支持向量机的分类效果，采用多元统计中的判别分析作为对比试验.判别分析是经典的多元统计方法，其主要思想是在分类确定的条件下，根据某一研究对象的各种特征值判别其类型归属问题的一种多变量统计分析方法.其基本原理是按照一定的判别准则，建立一个或多个判别函数，用研究对象的大量资料确定判别函数中的待定系数，并计算判别指标.据此即可确定某一样本属于哪一类.实验结果见表4.

表4 实验结果(1)

通过实验可以看出，多分类支持向量机模型较传统判别分析模型有着更好的分类能力.

4.2 模型的改进

考虑对多分类支持向量机模型进行改进，在如上的实验中均假设对错误分类的惩罚是一致的，但在实际情况中并不是如此.例如一种误差是将一名一等的学生错分为二等，即优秀的被判别成良好.另一种误差是将一等学生错分到五等，即将优秀的学生判别成差下.这两种错误的程度显然不一样，第二种错误较第一种错误要严重些，因此，可以调整惩罚矩阵Cjl，在本问题中最终用到的惩罚矩阵为

含义为将第i类学生错分到第j的惩罚为|i-j|.

基于此调整，训练得到新的分类器，实验结果如表5所示.

表5 改进后的实验结果

由模型的实验结果可以看出，分类结果精度较调整前有了较大的提高.

5 结论

1)本文基于多分类支持向量机算法建立了生源质量分析模型，该模型可以通过生源所在地、高考成绩，以及该成绩所在省的排名等信息，预测出该生源在大学毕业时学习情况的所处类别，因此可以对生源的质量优劣进行初步的分析和评价，对招生工作及相关政策的制定有一定的指导和帮助.

2)通过对惩罚矩阵进行合理的调整，模型的结果和可靠性都得到显著的提高.

［1］姚金琢.高等教育大众化与依法试行自主招生问题探析［J］.中国高教研究，2006(11)，90-91.

［2］于春梅，杨胜波，陈馨，等.SVM和基于PCA、PLS的 SVM在非线性辨识中的比较研究［J］.计算机应用研究，2004，24(6):85-90.

［3］VAPNIK V.The nature of statistical learning theory［M］.［S.l.］:Springer Verlag，1995.

［4］韩媚，郭丹凤.SVM的特征选择方法在高校就业预测中的应用研究［J］.杭州师范大学学报:自然科学版，2009，8(5):358-362.

［5］向小东，宋芳.基于核主成分与加权支持向量机的福建省城镇登记失业率预测［J］.系统工程理论与实践，2009，29(1):73-80.

［6］祁享年.支持向量机及其应用研究综述［J］.计算机工程，2004，30(10):6-9.

［7］SCHÖLKOPF，SMOLA A.Learning with Kernels［M］. Cambridge:MIT Press，2002.

［8］LEE Y K，LIN Y，WAHBA G.Multicategory support vector machines，theory，and application to the classification of microarray data and satellite radiance data［J］. Journal of the American statistical Association，2004，99 (465):67-381.

［9］CHEN D R，XIANG D H.The consistency of multicategory support vector machines［J］.Adv Comput Math，2006，24(1-4):155-169.

［10］窦智宙，平子良，冯文兵，等.多分类支持向量机分割彩色癌细胞图像［J］.计算机工程与应用，2009，45 (20)，236-239.

［11］康文雄，谢纪美，邓飞其，等.基于小波分解和多分类支持向量机的脸谱识别［J］.计算机测量与控制，2005，13(12):1390-1422.

［12］HSU C W，LIN C J.A Comparison of Methods for Multiclass Support Vector Machines［J］.IEEE Trans Neural Networks，2002，13(2):415-425.

［13］CHANG C C，LIN C J.LIBSVM:a library for support vector machines［EB/OL］.［2008-07-25］.http:// www.csie.ntu.edu.tw/～cjlin/libsvm.