基于小波分解的电力系统短期负荷预测方法研究

王成纲,郭 辉,张文静

(邯郸供电公司,河北 邯郸 056035)

0 引言

电力系统负荷预测是能量管理系统(EMS)的重要组成部分,是实现电力系统安全、经济运行的基础,是电力系统运行、控制和规划不可缺少的一部分。提高电网运行的安全性和经济性,改善电能质量,都依赖于准确的负荷预测。电力系统负荷预测,特别是提前24 h的短期负荷预测,对电力系统可靠、安全、经济运行具有重要意义。由于负荷本身的复杂性和不确定性,很难用一种数学模型将各种影响因素及其规律进行有效归纳,所以负荷预测精度的提高也受到影响。

尽管影响电力系统负荷的因素多种多样,但负荷仍较明显的具有日、周、月和年等周期性的变化特性,这种周期性从频域的角度来分析,可以把负荷序列看作多个具有不同频率分量的叠加[1]。由于小波分析在时域和频域上同时具有良好的局部化性质,能对不同的频率成分采用逐渐精细的采样步长,聚焦到信号的任意细节[2]。适当的小波变换能有效地分离和提取系统负荷不同的周期性、非线性和依赖关系,使每个变换序列都具有明显的规律性。因此通过对负荷序列进行小波分解,分析不同分解序列的特性并建立相匹配的模型进行预测,同时考虑到气象因素特别是温度因素的影响,对小波重构后的结果进行修正,可取得较高的负荷预测精度。

1 电力系统短期负荷预测

1.1 负荷数据预处理

为减轻不良数据对负荷预测模型的影响,应对原始负荷数据进行预处理。对原始数据进行数据的水平处理,即分析数据时,将前后2个时间的负荷数据作为基准,设定待处理数据的最大变动范围,当待处理数据超过这个范围时视为不良数据,应采用平均值的方法平稳其变化。具体实现:假设负荷序列用x(n)表示,n=1,2…,N,N表示取N天的负荷数据,通过下面两式求出 N天负荷的均值P及方差V:

定义ρ为负荷的偏离率,则:

在对负荷数据进行实际处理过程中,当负荷偏移率ρ大于1.1时,对该负荷数据进行修正,修正公式为式(4),采用式(4)中的x(n)来取代不良负荷数据x(n)。

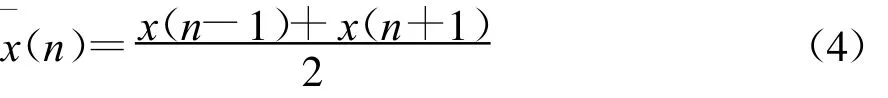
1.2日负荷数据的小波分解

通过小波变换能将负荷序列的不同频率分量分离出来,为了更好的表征负荷特性,采用小波分析方法对负荷序列进行小波分解。母小波以及尺度大小应根据负荷的特点进行选择,若尺度太小,负荷的某些变化特性如隐周期性可能无法体现,则无法得知负荷序列各频段详细信息;而在一定的预测要求下,尺度选的太大不但无法提高预测精度还会降低负荷预测的效率。母小波的选择是特殊的[3],应根据情况而定,一般有一些标准的小波可供选择。经过大量计算结果和实验证明,以3次中心B样条函数为小波函数,以2次样条函数为尺度函数,对负荷数据分解至尺度3是合适的。采用近似对称、光滑的紧支撑双正交小波db2(Daubechies函数)作为母小波,通过多分辨分析的Mallat算法对负荷数据进行三尺度分解。可将负荷数据分解为不同频率的特征分量。图1是2008年6月河北某地区前2周原始负荷序列和分解后的各频段分量,其中a0是负荷原始序列,a3是a0经过小波3层分解后的近似信号(低频部分),d1、d2和d3分别为a0各层分解的细节信号(高频部分)。

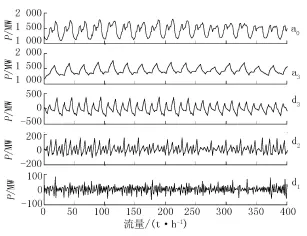
图1 原始负荷序列及其3层小波分解序列

1.3 人工神经网络模型

采用相匹配的人工神经网络BP模型对小波分解后的a3、d1、d2和d3分别进行预测。每个神经网络都为3层,即输入层、隐含层和输出层。由于对一天24时刻的负荷进行预测,因此对每个小波分解分量,分别构造24个规模较小的单输出网络,每个网络对应一点负荷值。

1.3.1 神经网络模型输入量的选取

利用BP神经网络进行预测时,输入量的选取是否合理直接影响BP网络的训练时间和预测精度。选取输入变量的原则是:在全面考虑各种重要影响因素的基础上,尽可能减少输入量的数目。设待预测时刻为第i天第t小时的负荷l(i,t),从图1中看出a3曲线平滑具有明显的日周期性,可见其同样应该具有周周期性,选取预测日前1天预测时刻及其前1时刻负荷l(i1,t)、l(i1,t1),预测日前2天相应2个时刻的负荷l(i2,t)、l(i2,t1),预测日前1天、前2天预测时刻的负荷变化量Δl(i,t),其中Δl(i,t)=l(i1,t)l(i2,t),预测日前1周、前2周预测时刻的负荷l(i7,t)、l(i14,t)、共8个变量作为输入变量。从图1看出d3具有半日周期性,选取预测时刻前124时刻的负荷,预测日前1天、前2天预测时刻前12时刻点负荷l(i1,t12)、l(i2,t12),预测日前2天预测时刻负荷l(i2,t),预测日前1周预测时刻的负荷l(i7,t)共28个变量作输入变量。图1中看出d2其日周期内嵌了4个短周期,选取预测时刻前124时刻的负荷,预测日前1天预测时刻前6时刻、前12时刻、前18时刻负荷l(i1,t6)、l(i1,t12)、l(i1,t18)以及预测日前1周预测时刻负荷l(i7,t)共28个变量作输入变量。而d1主要表现为随机分量,采用预测点前124时刻的负荷共24个变量作输入量。如果预测日前1天需要的时刻负荷数据未知,则所有数据向前推1天作为神经网络的输入量。

1.3.2 神经网络模型隐含层神经元个数的选择

对于隐含层神经元个数的选取,一般采用修剪的方法,开始时选择隐含层神经元的个数为一个较大的数M,对网络进行训练后,设当输入样本数据向量为Xi时,隐含层输出为(z1,i,z2,i,…,zM,i)(i= 1,2,…,N),令

则A为M阶实对称阵,可求得正交矩阵 P,使得:

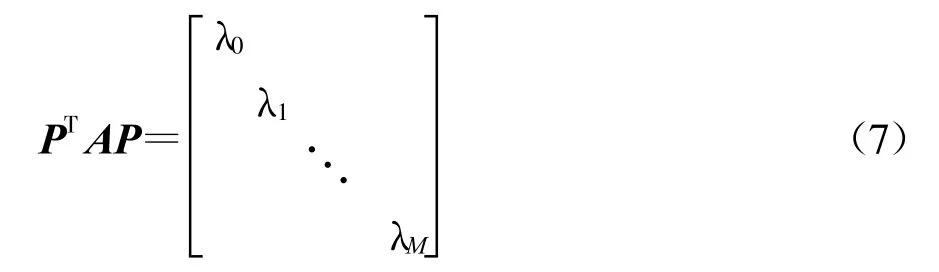
式中:λ0、λ1,…,λM为矩阵A的特征值。

令X=HP,则有

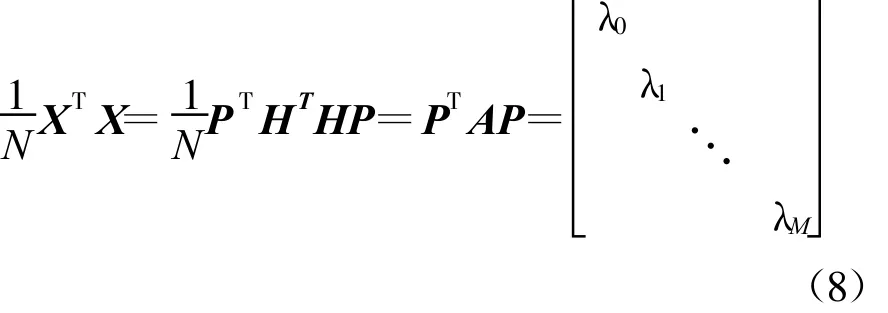
令X=(β0,β1…,βM),可知

因此若λi=0,则K‖βi‖2=ββ=0,即βi=0,此时有:

因此α0,α1,α2,…,aM线性相关。若A的特征值有m个为零,则X的秩为Mm,因此H的列向量线性无关的最大个数为Mm,这样隐含层神经元的个数选择为Mm,因此得到神经网络a3、d3、d2、d1模型的隐含层神经元个数分别为:8、15、15、15。

1.3.3 神经网络训练样本的选择

因为训练样本与预测负荷之间有强相关性,训练样本的选择需要结合负荷的特性,预测效果才精确。选择样本时,需要考虑的因素包括两方面:一是选择样本输入与样本输出的关系;二是选择合适的样本集。

训练样本可采用与待测日最接近的4周负荷数据,为简化模型并未考虑日期类型,即训练样本集中没有区分工作日和公休日。对训练样本集进行训练,在误差达到一定阀值下时确定网络连接权值,保留原权值,当误差超过一定阀值时,重新训练网络各权值。

1.3.4 神经网络算法的具体实现

在神经网络的基本结构确定后,就可利用输入输出样本集对网络进行训练。BP算法的训练就是对网络的权值和阀值进行学习和调整,使网络实现给定的输入输出的映射关系。而BP算法的实质是把一组样本输入输出问题转化为一个非线性优化问题,并通过梯度算法利用迭代运算求解权值问题的一种学习算法。经证明,具有sigmoid非线性函数的3层神经网络可以任意接近任何连续函数。

BP算法的基本步骤如下:

a.初始化权值W和阀值b,即把所有权值和阀值都设置成较小的随机数;

b.提供训练样本集,包括输入向量P和要求的预期输出T;

c.计算隐含层和输出层的输出;

隐含层的输出为:

输出层的输出为:

d.调整权值和阀值;

BP神经网络的权向量调整公式为:

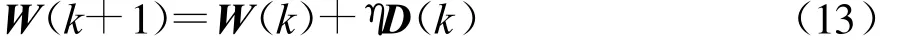
式中:W(k+1)、W(k)分别为(k+1)、k时刻的权向量;η是学习率;D(k)是k时刻的负梯度。按误差反向传播方向,从开始输出节点开始返回到隐含层按上式修正权值。阀值也是一个变化值,在修正权值的同时也修正阀值,原理同权值修正。

e.计算网络误差均方和E;

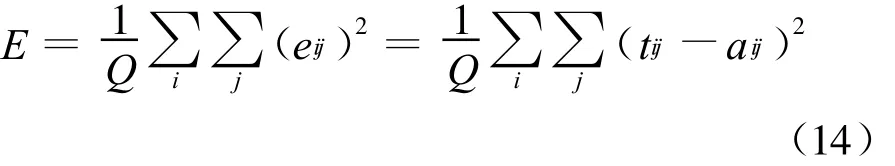
式中:Q为样本数。

f.循环步骤b到步骤e,直至误差均方和满足精度ε为止,即E＜ε。

1.4 线形回归模型的修正

电力系统负荷的变化受气象因素的影响,影响负荷分量的气象因素从直观上可考虑的有温度、湿度、降水、风力等。由于湿度、风力、降水的变化具有局部性,对电网的总负荷的影响总体上呈现随机性,同时也会使神经网络的学习负担过重,不利于模型的建立和实际使用[4]。为此只重点考虑温度变化的影响。

分析河北省某地区的温度和负荷数据,它们的关系近似于线性关系,尤其是温度高于30℃时。由于负荷的数值变化规律已在前面神经网络模型中的得到体现,因此可以忽略负荷因素只对温度建立一元线性回归模型,对小波重构后的结果进行修正。在一元线性回归模型中,温度设为自变量x,预测的负荷修正值设为y,两者的关系见式(15),其中a,b为不依赖于x的参数。

通常只对温度变化在2℃以上的天数进行调整,因此对参数a、b的估计要选取的样本来自于预测日前1个月内温度变化在2℃以上的天数,假设该天数为n,温度和负荷分别表示为{xi,i=1,2,…, n}和{yi,i=1,2,…,n},得到a、b的估计值a′、b′分别为:

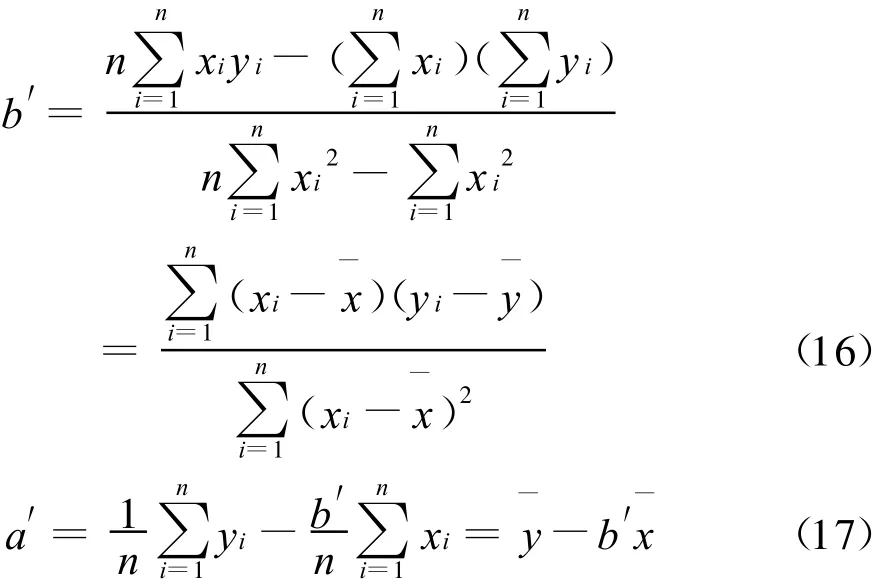
2 算例验证

本预测方法在进行预测时的具体步骤为:

a.对日负荷历史数据进行预处理;

b.对预处理后的负荷数据进行3层小波分解;

c.对分解后的各分量根据其特点分别采用相匹配的人工神经网络模型进行预测;

d.小波重构,考虑气象因素特别是温度的影响,建立一元线性回归模型对重构后的结果进行修正;

e.综合负荷预测结果,得到该日的负荷预测值。

建立的预测方法流程见图2。

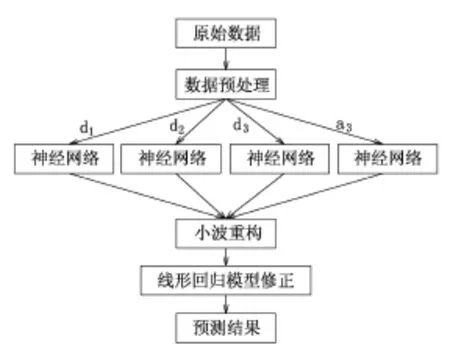
图2 预测方法流程

采用河北某地区数据对上述方法进行建模分析和测试。表1是上述方法与直接用BP法对1天24时刻负荷预测结果的比较,从表1所列测试结果可看出,采用上述方法进行负荷预测使负荷预测精度有了明显提高,表明该方法具有可行性。

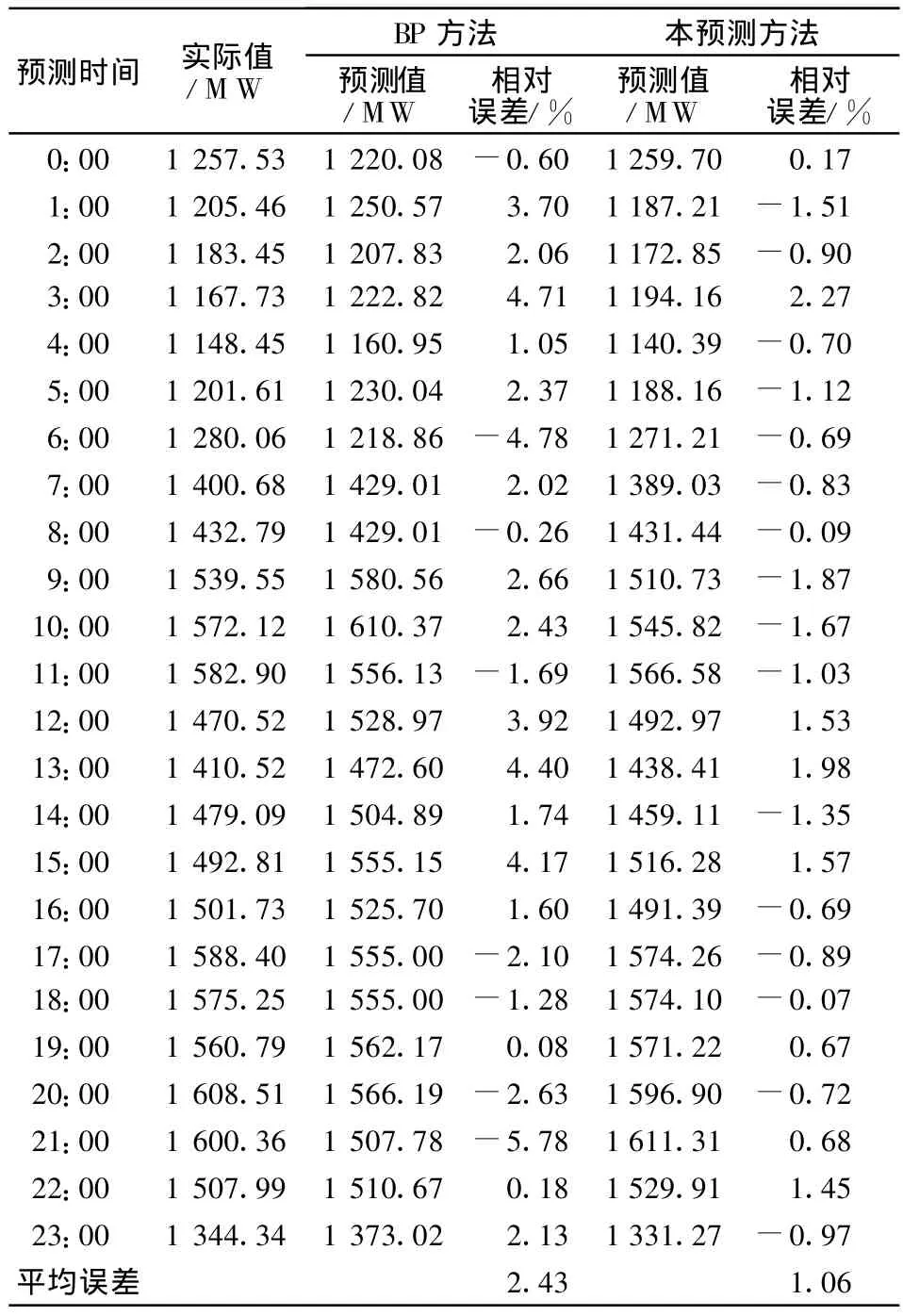
表1 人工神经网络BP法和本预测方法24 h负荷预测对比

3 结束语

在对负荷历史数据预处理的基础上,应用小波分解把负荷分解为多个频率分量,对每个频率分量分别进行分析,并采用与之相匹配的人工神经网络模型进行预测,小波重构神经网络预测结果。考虑到气象因素特别是温度的影响,也为了更好的提高负荷预测精度,采用一次线性回归模型对重构后的结果进行修正,最后综合得到负荷预测最终结果。通过对河北某地区的实际预测结果与直接用ANN模型进行预测结果的比较表明,该方法具有良好的预测精度。

[1] 牛东晓,曹树华,赵 磊,等.电力负荷预测技术及其应用[M].北京:中国电力出版社,1998.

[2] 彭玉华.小波分析与工程应用[M].北京:科学出版社,1999.

[3] 宋 超,黄民翔,叶剑斌.小波分析方法在电力系统短期负荷预测中的应用[J].电力系统及其自动化学报,2002,14(3):8-12.

[4] 康重庆,周安石,王 鹏,等.短期负荷预测中实时气象因素的影响分析及其处理策略[J].电网技术,2006,30(7):5-10.