汶川地震的6区域模型加速度峰值衰减关系

杨 帆,罗奇峰

（同济大学a.结构工程与防灾研究所;b.上海防灾救灾研究所,上海 200092）

目前,在加速度峰值衰减关系研究中主要存在2种思路：1）从原因出发,通过研究震源机制和地震动传播过程与加速度峰值衰减的理论关系,得到由更多细化参数控制的衰减关系式。这类方法从研究地震过程本质出发,对提高地震传播及衰减理论具有很强的指导意义。但是,由于地震过程本身的复杂性导致各参数间的相关影响,该方法必需依托庞于大量、精细的地震数据。如美国的NGA项目[2]下的3个工作团队得出衰减关系式[3-7]所用到的地震波描述参数则多达130个,这在世界大部分地区是无法实现的,不便于地震动衰减关系的工程应用。2）以实际得到的加速度等震线出发,研究衰减关系。为简化计算,该类方法以控制等震线的大体形状来抓住影响衰减关系的主因。目前基本上都使用圆模型,它将等震线近似的看作同心圆,以震中距或震源距为加速度等震线在测点位置方面的唯一控制参数,然而对于长断裂的大震而言,圆模型的加速度等震线和实际等震线偏差很大,例如图1[8]中汶川8级地震的烈度等震线形状就和圆模型明显相悖。需要特别指出,图1给出的是烈度等震线,它与加速度等震线还有一定区别,但可以认为两者存在近似的线性关系,同时也必须认识到这种关系比较模糊。该文利用烈度等震线代替加速度等震线的基本依据已经在文献[1]中详细阐述。鉴于圆模型的严重不足,在4区域椭圆模型的基础上提出了6区域模型,以便更加细致的刻画衰减关系的区域性特点。

图1 汶川地震烈度等值线图

1 4区域椭圆衰减模型的不足

4区域的椭圆模型以断层所在位置为长轴,以过断层中点并垂直于断层的方向为短轴,长短轴将整个观测区域分为4个部分。4个区域物理意义分别为：沿破裂方向前端的上下盘和沿破裂反方向末端的上下盘。其加速度的等值线示意图见图2,该方法忽略了断层长度垂直范围的2个区域,其等震线形状在断层范围内没有沿着断裂方向“发散开”的趋势,这导致前区椭圆看起来更加扁平,这与图1不符。由于破裂前端区域和末端区域共用短轴,短轴都是过断层中心,不能通过比较得到过断层不同位置处的短轴衰减关系来反映破裂方向对短轴衰减的影响。

图2 4区域椭圆模型加速度峰值等值线示意图

2 6区域衰减模型

由于4区域模型在等震线形状刻画和地震区域划分上的不足,该文采用下述划分方法：

以断层所在位置为长轴,以过断层2端点,且垂直与长轴的2条直线为短轴可以将等震线图分为6个基本区域。从图1可以看出：两端的4个区域曲线近似于椭圆,其形状由各自的长短轴控制。中间的2个区域曲线近似于直线。其形状由直线与断层2端点的断层距控制。

上述划分不仅在等震线图形上更加符合实际,而且所划分出的6个区域也具有明确的物理意义：断层垂直区域外,沿破裂方向前端的上下盘、断层垂直区域外,沿破裂反方向末端的上下盘以及断层垂直范围内的上下盘。

基于前文提到的烈度与加速度的线性关系,假设某几个值的加速度等震线（基准线）与烈度等震线形状相似,具体的控制指标是2种等值线在区域分割线方向上的截距相等,利用烈度等震线图量出这些截距,并由此作出加速度峰值的基准线。（图3）基准线间的其他等值线通过某种差值规律假设转化为求解方程的方法求得,其具体步骤如下：

图3 6区域模型加速度峰值等值线示意图

1）以断层（图3中间实线）所在直线为长轴,以过断层端点且垂直长轴的2条直线为短轴。分割线与等震线的截距标识为rij,i为基准线标号,j表示截取方向,取j=1,2,3,4,5,6。截距包含了两端4条椭圆线和中间段2条直线所需全部参数,可以由此得到基准线。

2）对于2基准线i和i-1间任意观测点的加速度等值线可由2条基准线差值算得。在理想状态下,2条基准线间应由无穷条不相交的等值线覆盖,在任意测点位置都有唯一一条加速度峰值等值线经过。同时等值线的形状应渐变过渡直至与基准线重合。满足下列2个条件的等值线符合这些要求：①它们都由4段不同的椭圆曲线和2段直线组成;②等震线在坐标轴正负方向上的截距为：

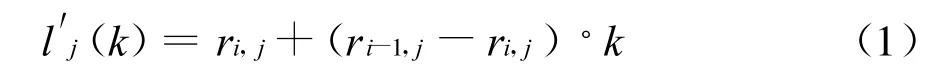
式中,k为自变量,0＜k＜1。这样可以保证当k从0到1时,加速度等值线的6个截距相对均匀增长,并保证当k=0,1时加速度等值线过渡为基准线形状。

如图3,以基准线i和i-1间的任意点h（x,y）的等值线作法为例。判断其所在象限,h（x,y）在第1区时,以l′1（k）为长轴、l′2（k）为短轴在一区范围内作椭圆;h（x,y）在第3区时,以l′4（k）为长轴、l′3（k）为短轴在3区范围内作椭圆;h（x,y）在第4区时 ,以l′4（k）为长轴 、l′5（k）为短轴在 4区范围内作椭圆;h（x,y）在第6区时,以l′1（k）为长轴、l′6（k）为短轴在 6区范围内作椭圆;将长短轴和h（x,y）点坐标带入到椭圆方程中,通分化简可以得到关于k的一元4次方程：

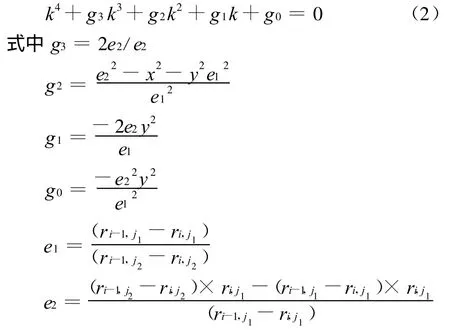
式中,j1取2个长轴即（j1=1,4）;j2取4个长轴即（j2=2,3,5,6）;其取值由h（x,y）所在象限决定。

h（x,y）在第2区或第5区时,K值直接由下式给出：

式中,j1取2个长轴即（j1=2,6）;j2取4个长轴即（j2=3,4）,其取值由h（x,y）所在象限决定。rn为断层半长。

通过求解式2和式3,得到任意位置点在（0,1）的范围内的唯一k值。将k代回到（1）式中即可求得等值线的6个截距。它是描述加速度等值线的完整参数,由其代替圆模型中的单一的震中距作为统计量进行拟合运算得到6个地震动加速度衰减关系。它们反映了6个区域中地震加速度衰减的基本特性。注意在求解方程式（2）时,应用一元4次方程的系数解[9]可以大大简化计算,提高计算速度和精度。

3 汶川8.0级地震的加速度峰值衰减关系曲线

以汶川8.0级地震,四川、陕西、甘肃、青海、宁夏、云南、山西7省公布[10]的261个土层加速度峰值记录为对象,拟合衰减关系曲线。

4区域椭圆模型的计算方法和过程文中不再给出,直接引用文献[1]中的相关结论于表2,以便用于结论分析及对比。

对于圆模型采用衰减关系式为[11-12]：

式中y为地震加速度峰值,R为震中距,R0为距离饱和因子,有：R0=k1 exp（k2◦M）,k1、k2直接按文献[13]结论取值,分别等于0.39、0.623,算得R0=57,a、b为回归系数。

相应6区域椭圆模型各方向半轴的衰减关系式为：

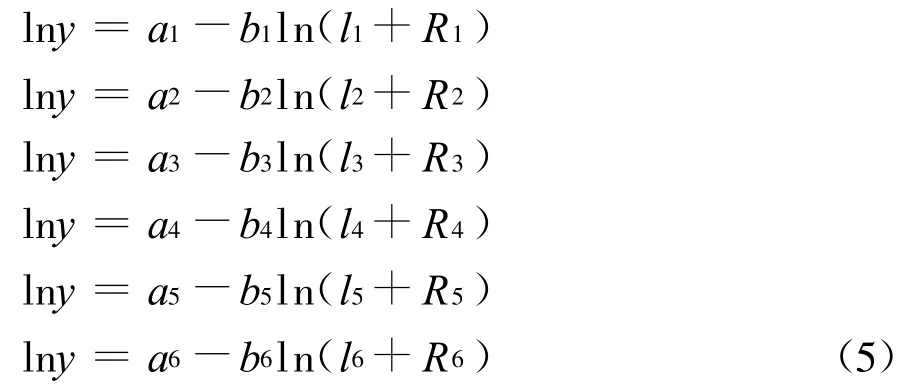
为保证震源体内加速度相等,采用联合椭圆模型[14-15]类似的方法计算,给出联合的衰减关系曲线式（6）。式中R1、R2、R3、R4、R5、R6为 6 个方向上的距离饱和因子,作为回归参数,通过式（5）采用最小二乘法,循环回归取方差为最小时对应的值。l1、l2、l3、l4、l5、l6为 6 个方向的半轴长,其值由式（1）、（2）、（3）求得,当其中任意一个按式（1）、（2）、（3）取值时,其它5个取为0,（1）、（2）、（3）式中ri,j在图 1中量出 。a、b1、b2、b3、b4、b5、b6 为回归系数 。

通过（6）式,采用最小二乘法,求得回归系数后各个方向的衰减关系由式（7）确定。

通过观测点坐标和震中坐标计算出测点震中距R,代入关系式（4）,利用最小二乘法得到圆模型的汶川地震水平向和竖向衰减曲线图4、5。拟合系数、饱和距离及拟合方差见表1。

图4 圆模型水平向加速度峰值衰减关系

图5 圆模型竖向加速度峰值衰减关系

通过式（1）、（2）、（3）得到观测点 4个方向的半轴长l1、l2、l3、l4、l5、l6 代入（5）式 ,通过循环回归得到饱和因子与方差关系图6、7,并取方差最小值为距离饱和因子。求得饱和因子后利用式（6）进行最小二乘拟合,求得回归系数,并带入式（7）求得4个半轴向的最终的衰减关系图8。

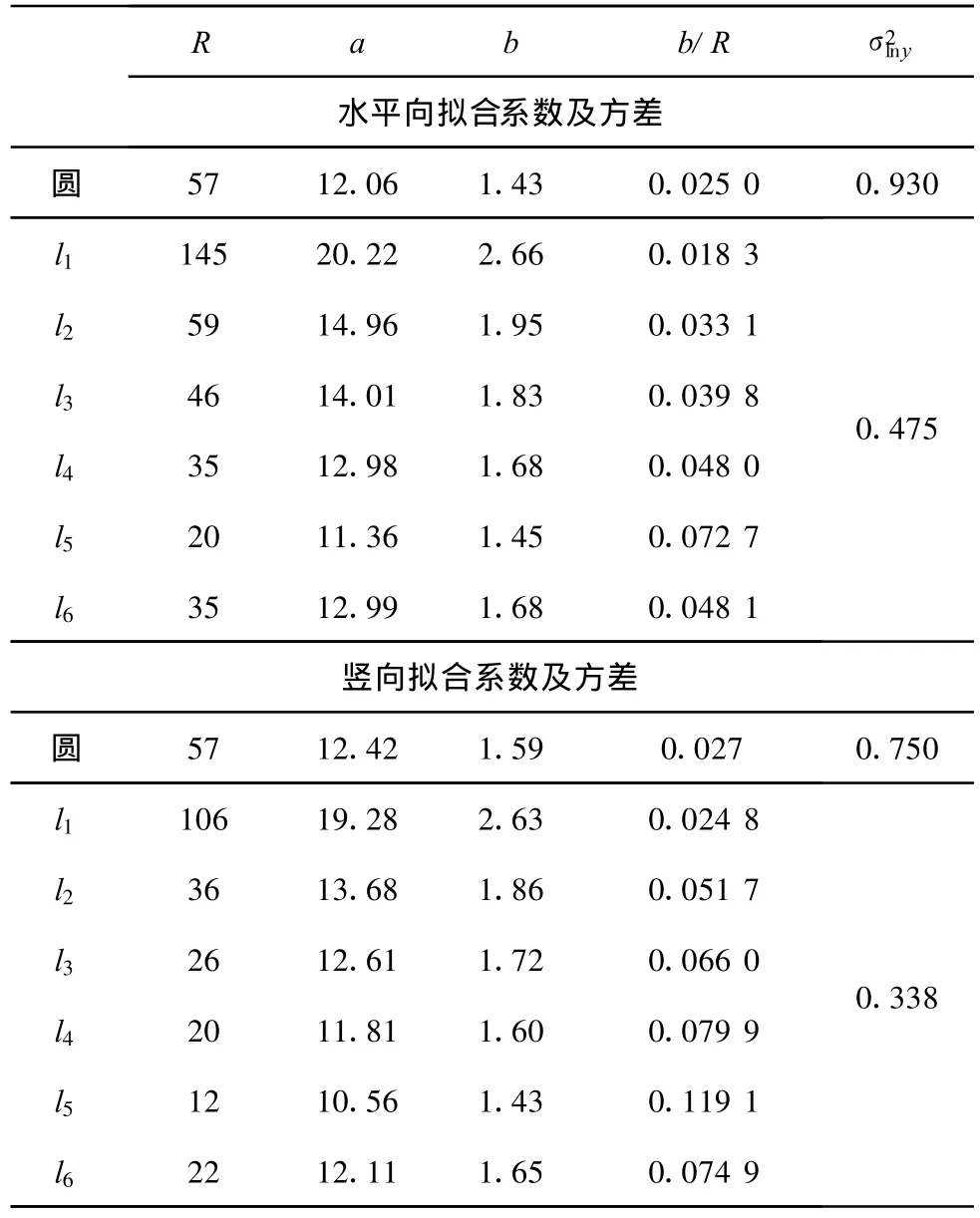
表1 6区域模型的拟合系数

表2 4区域椭圆模型的拟合系数

4 模型的对比及结论

观察图形可知,利用圆模型按震中距统计的观测点（图4、5）离散性较大,在近场时,该现象尤其明显;利用模型按6个方向的半轴长统计得到的数据点（图8、9）离散性小。从拟合方差上看,表1、2中圆模型的水平向和竖向拟合关系式方差分别为0.930、0.750;4区域椭圆模型方差为：0.490、0.340;该文模型的拟合关系式方差为0.475、0.338。后2者方差都比圆模型减小了1倍左右。而6区域模型比4区域模型方差略小,这说明结果更加符合实际。

图6 6区域模型水平向距离饱和因子

图8 6区域模型水平向衰减关系

6区域模型可以得到6条衰减关系,每相邻2条衰减关系代表了1个区域内加速度峰值衰减关系的上下限值。它可以反映破裂方向效应和上下盘效应。由衰减关系式2边对距离取导数可知,拟合系数b与震中饱和距离R之比是衡量近场衰减速度的关键。比值越小近场的衰减慢,反之亦然。该文称其为近场衰减速率系数。

从表1可以看出圆模型的近场衰减速率系数大小介于该文模型6个方向上的系数之间,可以认为圆模型是衰减速率在各方向的平均反应,对沿破裂方向的长轴l1衰减明显高估,这种方法是危险的。

就长轴而言,4区域椭圆模型与6区域得到的结论一致,l1和l4方向,v1和v3方向

的衰减关系各项拟合系数差别明显,从近场衰减速率系数上看,沿断层传播方向衰减慢,同时,它也是所有方向上衰减最慢的方向。

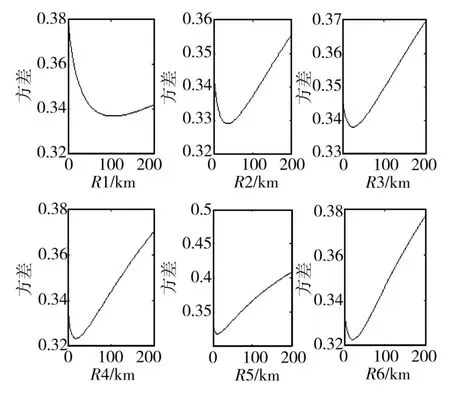
图7 6区域模型竖向距离饱和因子

图9 6区域线模型竖向衰减关系

就短轴而言,2种模型得到的结论有较大差别。从表2中可以看出,对4区域椭圆模型,v2和v4方向的衰减关系各项拟合系数以及近场衰减速率系数差别都很小,这1方面可能是由于汶川地震的倾滑成份较少引起的,同时还有另外1个原因：汶川地震的主断层在其长度中心处有一定距离的间断,由于间断距离与断层总长度相比很短,对间断处垂直范围以外的区域影响很小,才可以近似的将其看作一条连贯的断层。但是4段线模型的短轴经过了这个间断区域,在这里并没有实际上的断层,所以在该处得到的短轴衰减关系上下盘效应不明显。另外,4区域椭圆模型并不能体现破裂方向对短轴衰减关系的影响。

对于6区域模型,l6方向是过断层前端点,沿下盘垂直于断层方向的传播方向,l5方向是是过断层末端点,沿下盘垂直于断层方向的传播方向,从表1中可以看出l6衰减更慢,另外由于l6和l5的衰减关系存在差别,说明在区域5内的等值线与断层并不平行,除去断层距,观测点与断层的垂足在断层上所处的位置对短轴方向的地震衰减也有影响。研究l2和l3可以在上盘得到同样的结论。

l6和l2的垂足均为断层前端,且也是垂直与断层方向,唯一的不同是,l6沿下盘传播而l2沿上盘传播,对比两者的近场衰减系数可知,在该断层位置,汶川地震上盘的近场衰减更慢,对比l3和l5可以得到相同结论。

对比在任意方向上的竖向近场衰减系数都比同方向上的水平向衰减系数大,即竖向衰减快。

[1]杨帆.罗奇峰.基于4区域椭圆模型的汶川8.0级地震加速度峰值衰减关系拟合[J].振动与冲击.2010,29（5）：136-140.

YANG FAN,LUO Q I-FENG.Wenchuan8.0 magnitude earthquake acceleration peak attenuation curve using four-area e llip tical mode[J].Journal o f V ibration and Shock,2010,29（5）：136-140.

[2]陶夏新.孙晓丹.陶正如.对新一代地震动衰减关系研究看法[C]//第七届全国地震工程学术会议论文集.2006.

[3]ABRAH AMSON N A,YOUNGS R R.（1992）.A stab le algorithm for regression analyses using the random effects model Bull[J].Seism.Soc.Am.1992,82：505-510.

[4]CAM PBELL K W,BOZORGNIA Y.Cam pbell-Bozorgnia next generation attenuation（NGA）relations for PGA,PGV and spectral acceleration：A p rogress report[C]//Proc.of the 8th U.S.National Conf on Earthquake Engineering（8NCEE）,San Francisco,USA,2006.

[5]CHIOU B,DARRAGH R,SILVA W.An overview of the NGA strong-motion dataset[C]//Abstrac ts o f the Centennial M eeting o f the Seismologica l Society of A-merica,San Francisco,2006.

[6]CH IOU B,R YOUNGS.PEER-NGA empirical ground motionmodel for horizontal spectral accelerations from earthquakesin active tectonic regions[C]//Abstracts of the Centennial Meeting o f the Seismological Society of America,San F rancisco,USA,2006.

[7]POW ER M,BCH IOU N A BRAHMSON,ROBLEE C.The“Next generation of ground motion attenuation models”（NGA）project[C]//An Overview,Proc.of the 8th U.S.National Con f.on Earthquake Engineering（8NCEE）,San Francisco,USA,2006.

[8]地震工程与工程振动编辑委员会.汶川8.0级地震工程震害概览[M].北京：科学出版社,2008,10：15-20.

[9]Laubenbacher R, Pengelley D. Mathematical Expeditions[M].New York：Sp ringer-Verlag Inc,1999.

[10]中国地震局震害防御司.汶川8.0级地震未校正加速度记录[M].北京：地震出版社.2008.9.

[11]CAMPBELL K W.1981.Near 2 source attenuation of peak ho rizontal acceleration[J].BSSA,1981,71（6）：2039-2074.

[12]雷建成,高孟潭,俞言详.四川及临区地震动衰减关系[J].地震学报,2007.29（5）：500-511.

LEI JIAN-CHEN,GAO M ENG-TAN,YU YANXIANG.Seism ic motion attenuation relations in sichuan and adjacent areas[J].A cta Seisologica Sinica,2007,29（5）：500-511.

[13]黄慧华.近源地震动峰值加速度衰减关系影响因素分析[J].工程地质学报,1998.6（1）：38-41.

HUANG HU I-HUA.Analysis of influenceo f factors on attenutiion relation of near source ground motion peak acceleration[J].Journal of Engineering Geology,1998,6（1）：61-66.

[14]Cornell C A.Engineer Seism ic Risk Analysis[J].BSSA,1968,58（5）：1583-1606.

[15]姜慧.新疆地震烈度的椭圆衰减关系研究[J].高原地震,15（4）：47-50.

JIANG HU I.Study on the ellip tic attenution of seism ic intensity in xinjiang[J].Earthquake Research In Plateau,1993,5（4）90：96.

（编辑胡 玲）