非线性破坏准则下岩石地基承载力的影响因素

张国祥,李丽民,,张成平,曹 鑫

（1.中南大学土木建筑学院,长沙 410075;2.湖南城市学院,湖南益阳 413000;3.北京交通大学隧道及地下工程教育部工程研究中心,北京 100044）

地基稳定性是地基设计中必须考虑的一个重要因素,它不仅控制建筑物的安全,而且客观上影响工程的经济合理性。因此,合理确定地基承载力,弄清其影响因素,对高层建筑、水利水电、铁路、公路工程等各种建筑尤为必要。确定地基承载力,一般有现场原位试验、理论公式以及从地基承载力表中查取3种计算方法。对地基承载力、承载力系数的理论公式研究主要分为3类：一类是以Prandtl-Reissner为代表的滑移线理论,这种方法没有考虑土体重量对地基存承载的影响;一类是以 Terzahgi与Meyerhof等学者为代表的极限平衡法,承载力系数Nq和N c采用平衡方程方法获得,而承载力系数Nγ采用经验法获得;另一类是 M ichalow ski（1997年）[3]等学者根据上限定理,在相同破坏机制的条件下,对承载力系数Nq、Nc和Nγ进行研究。但他们的研究都局限于线性M ohr-Coulomb破坏准则。岩土材料的非线性强度是一个非常突出不可忽视的材料强度特性问题,非线性严重影响岩土工程的力学行为,但对于非线性强度准则下的地基承载力的研究还很少。有人提出简单地将非线性强度准则线性平均化,按M ohr-Coulom b线性强度准则确定地基承载力。后来有人提出用单一切线法将非线性强度准则线性化[4-5],然后再按线性强度准则确定地基承载力,只是强度指标随切点位置而变,实际上是假定求解区域的法向应力相同,这与实际不符。文献[2]给出了H oek-Brown破坏准则下的地基承载力上下限有限元解,并且非常接近,可以认为它们的平均值接近理论解。在上下限有限单元求解过程中,线性强度准则的处理非常困难,非线性强度准则的处理更加困难,文献[3]中并沒有介绍如何处理非线性强度准则问题。影响岩石地基极限承载力的因素极其复杂,无论是传统的理论计算还是现场试验都会存在一定的局限性,目前对于岩石地基承载力的理论研究还很少。因此,该文考虑岩土材料的非线性破坏准则,运用上限理论[6-7]和多个刚性滑块破坏机构对岩石地基承载力的影响因素进行研究,提出了一种多切线法来处理非线性强度问题,多切线法能充分考虑实际的非均匀应力分布,当刚性滑块细分后,是一种严格意义上的非线性极限分析方法。

1 非线性修正Hoek-Brown破坏准则

为排除岩石各向异性的影响,主要分析的是完整岩体和破碎岩体,他们符合Hoek-Brown非线性破坏准则的要求。Hoek.E和Brown.E.T[8-10]通过大量实验提出了一种非线性破坏准则,并对其不断的改进和发展,已得到工程界广泛认可。其数学表达式为：

式中m,s为岩体特性参数;σc为岩块的单轴抗压强度;σ1和σ3分别为岩体破坏时的最大、最小主应力,a为与岩石完整程度有关的参数。其中m,s由岩石评分系统GSI来确定：

式中系数mi可以通过不同围压下的三轴试验确定,一般其变化范围为4～33左右。D为岩石的扰动系数,对于完整岩体取0,极破碎岩体取1.0,其它内插确定。为适应传统分析方法的需要,需要将Hoek-Brow n参数转化为Mohr-Cou lomb参数φ,c。为方便计算,需要建立φ,c之间的关系式,该文采用切线法,即在Hoek-Brown破坏曲线上取一点作其切线,如图1所示`,其切线方程为：

由于φ,c值的大小与滑动面上的法向应力σn有关,所以在地基中的不同位置,由于σn的不同而导致φ,c值的不同,φ,c值均为瞬时值而不是常量,记为ct、φt。经推导可得ct、φt之间的关系为[6]：

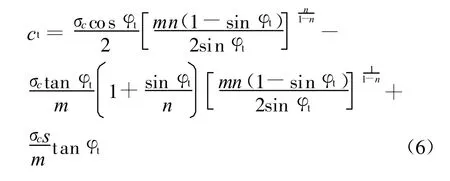
2 岩石地基承载力上限分析

该文采用多刚块法[11-12]和多切线法研究岩石地基承载力问题,切线法得到的强度值实际上是超过了材料的真实强度,得到的解为极限荷载的上限解[5,13]。将地基分成刚性滑块,然后采用非线性Hoek-Brown破坏准则,划分示意图如图2。由于基础两侧地基的划分方式一致,故只给出了一侧的划分示意图,计算时也只需取一半计算即可。由几何

和φt,在非线性强度曲线上寻找到最恰当的若干条外切直线,通过切线引入多组变量Ct和φt使得此时的岩石地基承载力最小。

图1 Hoek-Brown破坏准则曲线的切线

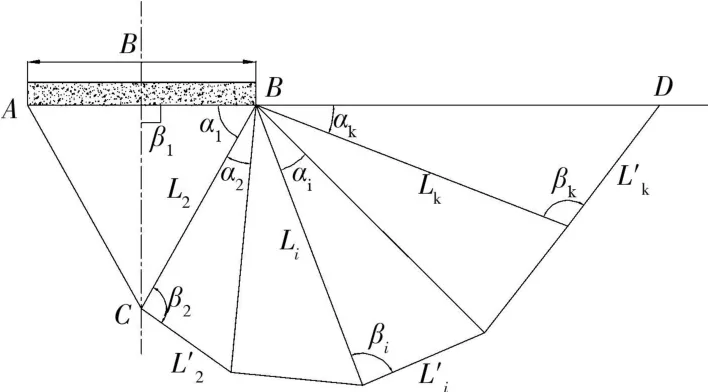
图2 地基单元划分示意图

根据相关联流动的正交流动法则,刚体平移时位移速度与刚体界面必成φi角。但由于不同单元边界处的应力状态不同,故φi角的取值也是不同的,因此三角形公共边上的瞬时摩擦角为φi,黏聚力为ci,而底边的瞬时摩擦角为 φ′i,黏聚力为c′i。由于三角形单元公共边处存在速度不连续面,因此每条公共边上的速度都是相对的,并假定塑性功的耗散只发生在三角形公共边和底边上。每个三角形刚块形状由边长Li,L′i,夹角 αi,βi控制,Vi为第i块刚体的绝对速度,Vi-1,i为第i-1号块与第i号块间的相对速度。速度场应符合如图4所示几何关系,由图2、图3和图4可得到：

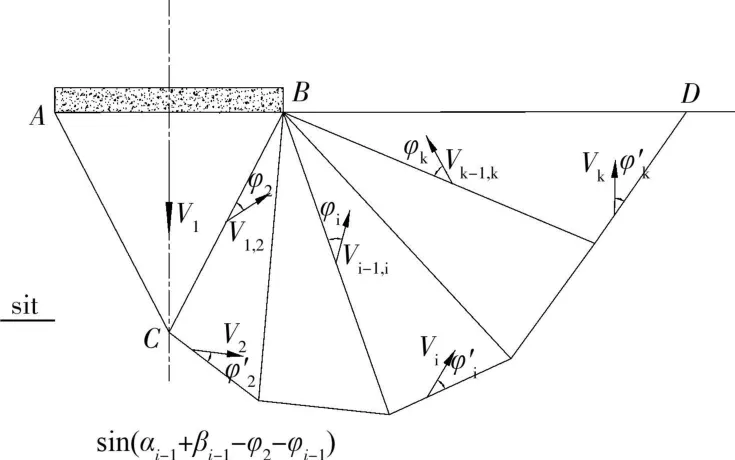
图3 地基单元速度场示意图

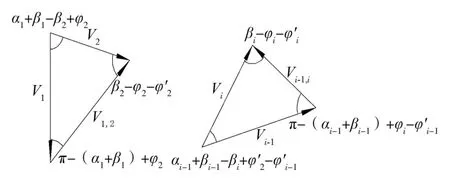
图4 第1号单元和第i号单元速度矢量图

2.1 内能耗散率

由于内能的耗散仅发生在速度不连续面上,即三角形单元的公共边和底边上,故内能耗散率为：

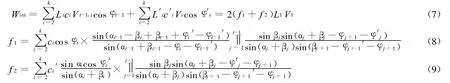
2.2 外力做功功率

考虑基底岩体的自重,则外力的做功包括重力、超载和极限荷载的做功,下面分别计算它们的功率。

2.2.1 重力功率 设基础的宽度为B,岩石的重度为 γ。则重力功率为：

2.2.2 超载功率 设地面的均布荷载为q,分布的范围为第k号三角形单元的边长Lk+1,位移方向为第k号三角形单元的绝对速度方向,则超载功率为：

2.2.3 极限荷载功率 极限荷载作用于1号单元上,方向与1号单元的绝对速度V1方向一致,故其功率为：

2.3 极限分析上限解的求解

在式（17）中,B、γ、q都是已知量,极限承载力qu仅与f1、f2、f3和f4有关。而由f1、f2、f3和f4的表达式可以看出,它们分别是所有的三角形单元几何参数和岩石物理参数的函数,取决于变量αi、βi和φi、φ′i及Ci、C′i的大小 。岩石地基的划分单元数为K个单元数时,共有4K个变量。但由式（5）式和（6）式可以看出 ,φ、φ′i和Ci、C′i满足一定的关系,并且这些变量应满足以下几何约束条件和速度场约束条βi+φ′i-φ′i-1 ≤π。不同的变量和变量组合能得到不同的极限土压力上限解,由于极限分析上限解总是大于真实极限荷载的,所以在上限解中,岩石地基承载土越小,越接近真正的极限荷载值,岩石地基承载力的求解实际上是一个求最小值的问题。本文利用M atlab软件平台,采用非线性 “序列二次规划”优化方法,编制相应程序来获取岩石地基承载力的上限解。

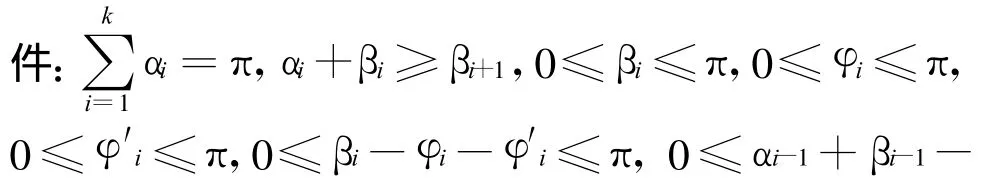
3 计算方法的可行性

引入一个地基承载力系数Nσ来评价地基极限承载力的大小。对于如图2所示的宽度为B的条形基础,岩石地基材料的轴向抗压强度为σci,岩石的地质强度指数由GSI指标来衡量,岩石地基材料的重度为γ,岩石特征参数为mi,则地基的极限承载力可写为：

若忽略岩石地基材料的自重,则可用Nσ0来代替Nσ。采用与前人的研究成果进行对比的方法来验证该方法的可行性,对比结果见表1和图5。文献[1]中,作者采用单切线法来求解Hoek-Brown破坏准则下的地基承载力上限解,文献[2]给出了Hoek-Brown破坏准则下的地基承载力的上下限有限元解,其上下限解之差在5%左右,可以认为它们的平均值已经很接近理论解。因此,从对比结果可知：单切线法计算的结果明显大于该文的计算结果,最大的差别能达到179.3%,而随着GSI的增加差别有所减小,但最小的差别也能达到37.6%,若直接采用切线法来计算地基承载力上限解时需要设置较高的安全系数方可,否则将导致非常大的误差,Hoek建议在用切线法得到的c值在采用时应至少折减25%;该文计算的结果与理论解已经非常接近,完全能满足实际工程的要求,并且较之上下限有限元法该文所述的方法则显得更加简单奏效,具有一定的实用价值。

表1 不同GSI和mi下地基承载力系数计算结果（q0=0,D=0,γ=0）

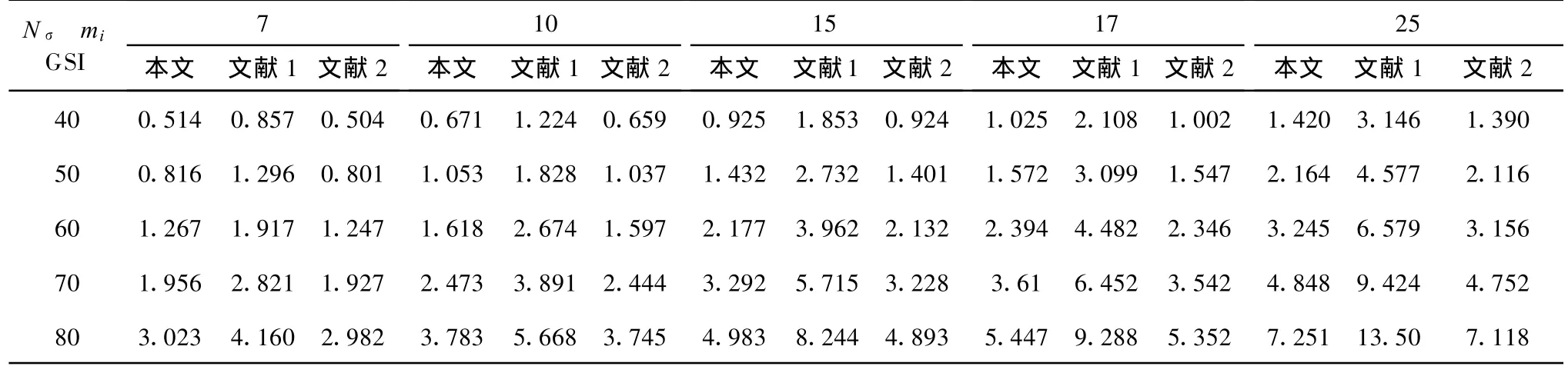
续表1

图5 地基承载力系数Nσ的比较

4 计算结果的分析

采用上述方法对地质强度指标GSI、完整岩石岩性系数mi、自重γ、超载q和扰动系数D对岩石地基承载力的影响进行研究。自重对地基承载力系数的影响（q=0,D=0）的计算结果见图6,超载对地基承载力系数的影响（γ=0,D=0）的计算结果见图7,开挖扰动系数D对地基承载力的影响（γ=0,q=0）的计算结果见图8。

由计算结果分析发现：在其他条件不变时,改变m i、GSI、超载q和自重γ中间的任何一个参数,地基承载力系数都是随它的增大而增大。当GSI值较小时,自重γ、超载q对地基承载力系数影响很大,当GSI较大时,自重γ、超载q对地基承载力影响不大,说明自重γ、超载q地基承载力是有一定贡献的,然而岩石地基承载力的大小主要还是取决于岩石的GSI和mi。当岩石较完整时,其自身的粘聚力和摩擦角都较大,地基承载力也相应较大。在其他条件不变时,地基承载力系数随着开挖扰动系数D的增加而减小,随GSI的增加,开挖扰动系数对地基承载力的影响力也在不断的减小影响,当GSI=100时,开挖扰动对地基承载力几乎没有影响。

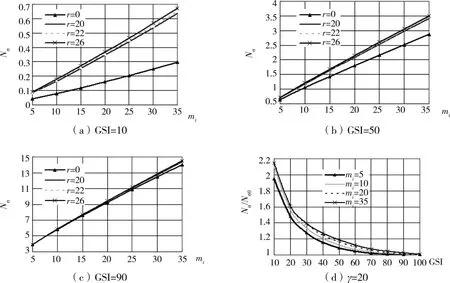
图6 自重对地基承载力系数的影响（γ单位为KN/m3）

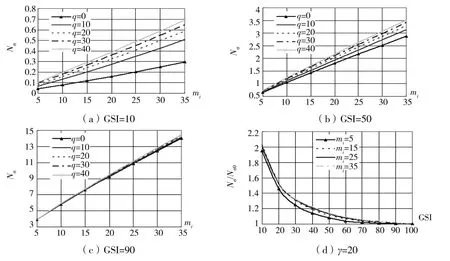
图7 超载对地基承载力系数的影响（q单位为KN/m2）

图8 开挖扰动系数对地基承载力系数的影响

5 结论

地基承载力问题是岩土工程领域中的基础性课题之,正确地评价承载力的大小,对于确保工程安全至关重要,它一直深受国内外学者的关注[15-17]。对于岩土材料而言,引入非线性强度曲线假设是非常必要的,因为非线性破坏准则更合工程的实际情况,也被许多学者的试验成果所证实。目前地基承载力理论计算大多采用线性破坏准则,该文在上限定理的基础上,采用Hoek-Brown非线性破坏准则和“多切线法”,利用M atlab软件平台和非线性“序列二次规划”优化方法,编制相应程序来计算岩石地基的承载力,分析岩石地基承载力的影响因素。计算结果表明：

1）该文计算的结果与上下限有限元法得出的结果极为接近,完全能满足实际工程的要求,并且较之上下限有限元法更加简单奏效,具有一定的实用价值。

2）单切线法没有考虑地基不同位置由于法线应力 σn的不同而导致Ct、φt值的不同,计算结果偏大,在实践中使用会带来较大的风险。

3）岩石地基承载力的大小主要取决于岩石的GSI和m i,自重 γ、超载q和开挖扰动系数D对岩石地基承载能力有一定影响,GSI值较小时,自重γ、超载q、开挖扰动系数D对岩石地基承载力影响很大,GSI较大时,自重 γ、超载q和开挖扰动系数D对岩石地基承载力影响不大。

[1]YANG XIAO-LI,YIN JIAN-HUA.Upper bound solution for ultimate bearing capacity with a modified H oek-Brow n failure criterion[J].Int.J.Rock.Mech.Sci,2005,42：550-560.

[2]M ERRIFIELD R S,LYAM INB A V.Lim it analysis solutions for the bearing capacity of rock masses using the generalized Hoek-Brown criterion [J].International Journal of Rock Mechanics&M ining Sciences,2006,43（6）：920-937.

[3]M ICHALOWSKIR L.An estimate of the influence of soil weight on bearing capacity using lim it analysis[J].Soils and Foundations,2007,37（4）：57-64.

[4]HOEK E.Estimating Mohr-Coulomb friction and cohesion values from the H oek-Brow n failure criterion[J].International Journal of Rock Mechanics&M ining Sciences,2008,27（3）：227-229.

[5]CA I M,KA ISER P K,TASAKA Y,et a l.Determ ination of residual strength of jointed rock masses using theGSIsystem[J].International Journal of Rock Mechanics and m ining Sciences,2007,44（2）：247-265.

[6]HOEK E,CARRANZE-TORRES C,CORKUM B.H oek-Brow n failure criterion–2002 edition[C]//Proceedings of the North American Rock Mechanics Society Meeting.Toronto,2002：267-273.

[7]YANG XIAO-lI.Upper bound lim it analysis of active earth p ressure considering different fracture surface with non linear yield criterion[J].Theoretical and App lied Fracture Mechanics,2007,47（1）：46-56.

[8]HOEK E.A brief history of the development of the H oek-Brow n failure c riterion[EB/OL].H ttp：//www.rocscience.com,2004.

[9]HOEK E,BROWN E T.Empirical strength criterion for rock masses[J].J Geotech Eng Division,American Society of Civil Engineers,2001,106（1）：128-135.

[10]HOEK E,WOOD D,SHAH S.A modified Hoek-Brow n criterion for jointed rock masses[C]//Proceeding o f Rock Characterization.Sym posium of ISRM：Eurock 92.1992：09-213.

[11]SOUBRA A H.Upper-bound so lutions for bearing capacity of foundations[J].Journal of Geotechnical and Geoen vironmental Engineering,2004,125（1）：59-68.

[12]YANG XIAO-lI,YIN JIAN-HUA.Upper bound so lution for ultimate bearing capacity w ith a modified Hoek-Brown failure criterion[J].International Journal of Rock Mechanics and M ining Sciences,2005,42（4）：550-560.

[13]杨小礼.岩石极限分析非线性理论及其应用[J].中南大学学报：自然科学版,2009,40（1）：225-229.

YANG X IAO-LI.Lim it ana lysis with non linear failure criterion in rock masses and its app lications[J].Journal of Central South University：Science and Technology,2009,40（1）：225-229.

[14]SERRANO A,OLALLA C,GONZALEZ J.Ultimate bearing capacity of rock masses based on themodified Hoek-Brown criterion[J].Int.J.Rock Mech M in Sci.2000,37（6）：1013-1018.

[15]梅岭,梅国雄,宋林辉,等.基于三维破坏面的地基极限承载力计算方法[J].水文地质工程地质,2009,36（2）：52-56.

M EI LING,MEIGUO-XIONG,SONG LIN-HU I,etal.M ethod for the calculation of ultimate bearing capacity o f foundation based on 3D failure sufrace[J].Hydrogeology&Engineering Geology,2009,36（2）：52-56.

[16]梅岭,梅国雄,宰金珉.埋深基础地基极限承载力的数值求解方法[J].岩土力学,2009,30（6）：1810-1814.

MEI LING,M EI GUO-XIONG,ZA I JIN-M IN.Numerica l anaysis of ultimate bearing capacity of ground with deep buried foundation[J].Rock and soil M echanics,2009,30（6）：1810-1814.

[17]秦会来,黄茂松.双层地基极限承载力的极限分析上限法[J].岩土工程学报,2008,30（4）：611-616.

QIN HUI-LA I,HUANG MAO-SONG.Numerical analysis of ultimate bearing capacity of ground w ith deep buried foundation[J].Rock and Soil Mechanics,2008,30（4）：611-616.

（编辑王秀玲）