以舱段模型代替整艇模型进行噪声估算的可行性探讨

王路才 周其斗 纪 刚 谢志勇 莫登沅

海军工程大学 船舶与动力学院，湖北 武 汉 430033

以舱段模型代替整艇模型进行噪声估算的可行性探讨

王路才 周其斗 纪 刚 谢志勇 莫登沅

海军工程大学 船舶与动力学院，湖北 武 汉 430033

采用结构有限元耦合流体边界元的附加质量附加阻尼算法，对SUBOFF潜艇模型的一个舱段在考虑不同声反射边界条件下的水下辐射噪声进行了数值计算，并讨论了以舱段模型代替整艇模型进行噪声估算的可行性。分析结果表明，不同声反射边界条件下辐射噪声的指向性比较一致，但不同边界条件下辐射噪声的最大声压级误差较大，声反射边界条件对舱段模型辐射噪声的影响不可以简单忽略，为对不同潜艇结构进行噪声估算提供了参考。

流固耦合；有限元；边界元；辐射噪声

1 引言

水下弹性结构振动和辐射噪声对于水中兵器和舰艇隐身具有非常重要的意义。对于弹性结构的振动，由于其结构的复杂性，使我们不得不采用有限元方法。目前，很多有限元商用程序在分析各种大型结构的动力特性中都得到了广泛的应用［1］，这些商用软件通常具备处理内域流体与结构耦合的噪声分析功能，因此对内域声场问题，采用结构有限元耦合流体有限元是一种可行的方法［2］。然而采用有限元方法分析外域流体与结构的声耦合问题时遇到了一个需要在较大区域划分流体有限元网格和满足无穷远辐射条件的困难，这种方法一般要求电子计算机有较大的容量，并且计算时间较长，给实际计算带来了困难［3］。一般认为，采用结构有限元耦合流体边界元方法是解决外域流体与结构声耦合问题的最佳途径，并且这种方法在舰船水下辐射噪声的计算中得到了广泛的应用［4－8］，这是因为边界元只需在流固耦合面上划分边界元网格，远场声辐射条件可通过选取格林函数自动满足。文献［9-10］提出了一种采用结构有限元耦合流体边界元计算水下结构声辐射问题的方法——附加质量阻尼法，该方法采用由流体到结构进行解耦的方式实现流固耦合问题的解耦。文献［11］依据不同分析域的特点，对结构域和流体内域采用有限元方法，对流体外域采用边界元方法，研发了大型水下结构流固耦合振动与声辐射的计算程序，同时实现了流体内域和流体外域同结构的耦合计算。采用附加质量阻尼法的好处在于可以通过FORTRAN和DMAP语言混合编程实现流固耦合问题的解耦，并利用NASTRAN软件实现流固耦合计算［12］。虽然文献［12］宣称该方法可以实现潜艇这样的大型结构流固耦合振动和声辐射问题的预报，但是对于潜艇这样的复杂结构，整艇建模计算仍然需要耗费很大的人力物力，计算代价很大。

实际工程应用中，由于整艇计算的代价太高，计算时间太长，因此，有学者试图采用潜艇的一个舱段结构模型代替整艇模型进行计算，以便在方案设计阶段快速地预估结构和隔振参数。以潜艇舱段替代整艇将会导致3个方面的差别：

1）潜艇整艇结构振动时，舱段结构振动将会由舱段部分向其他部分传递；而采用独立的潜艇舱段模型取代整艇进行计算，舱段以外的艇体振动辐射噪声将被舱段两端的舱壁振动辐射噪声所取代；

2）舱段模型两端舱壁的圆周处是自由振动的边界条件，而实际潜艇在此处存在由相邻的结构所施加的弹性边界条件，这将导致舱段结构被激振动时湿表面振动的差别，从而产生辐射噪声的差别；

3）潜艇舱段以外的其他部分作为水中存在的几何形状对舱段自身辐射噪声存在声反射影响，该影响在舱段模型中将被两端的舱壁所取代。

前两点的差别是由于舱段结构与整艇结构不同导致振动不同所引起，第3点则是由于两者声反射面不同而引起。本文是这一探讨的第一步，主要讨论前述差别的第3点，即潜艇舱段以外其他部分声反射特性对舱段模型自身辐射噪声的影响。

本文首先对SUBOFF潜艇模型的中间一个舱段以及头尾舱的湿表面进行建模，采用结构有限元耦合流体边界元的附加质量附加阻尼算法计算其在考虑潜艇舱段以外的其他部分声反射情况下该舱段的辐射噪声，比较探讨潜艇舱段以外反射面对舱段自身辐射噪声的影响。计算中，本文对潜艇舱段以外的部分做了不同程度的简化，设置了不同的反射边界，用于考察不同反射边界对舱段辐射噪声的作用。通过对考虑各种不同反射边界条件下辐射效果的分析和比较，给出舱段模型对反射边界条件影响的变化规律，本文只是这一变化规律探讨的初步尝试。

2 SUBOFF潜艇舱段水下振动与声辐射数学模型

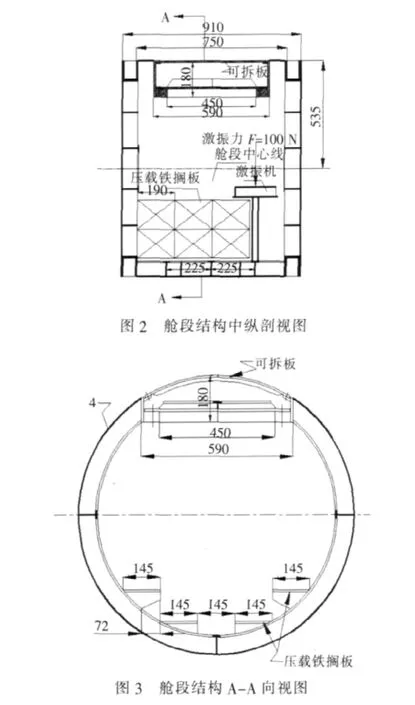
SUBOFF潜艇模型是美国国防部高级研究计划署（DARPA）资助的SUBOFF计划所使用的模型，本文所用模型是在标准模型的基础上，进行了部分改变，并参考现有SUBOFF试验模型艇，其艇长为9.621 m。图1中A所示为整艇模型，该模型分为3段，本文只对中间一个舱段进行完全建模。图1中B所示为舱段模型，头尾两个舱段建其壳体模型，舱段的几何尺寸见表1。图2、图3为舱段结构图，结构中设有22块压载铁搁板，每块压载铁搁板上放置1块压载铁，单块压载铁的质量为23.3 kg，模型为钢质结构，本文计算所使用的钢材材料参数见表1。

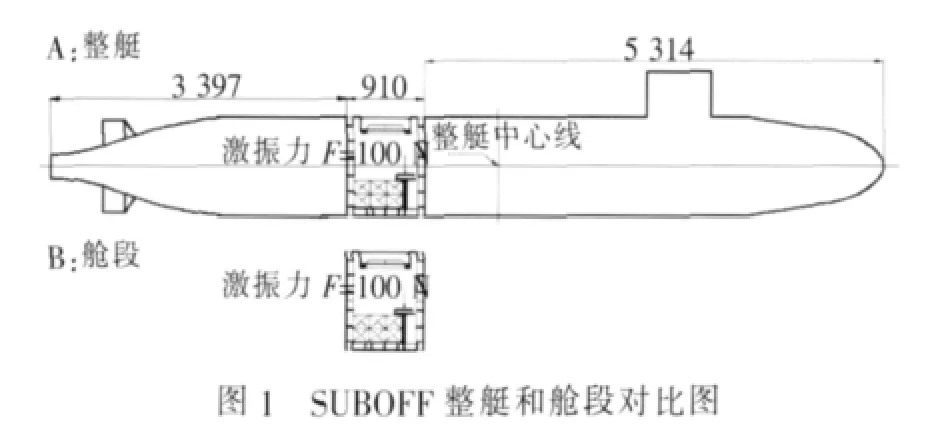
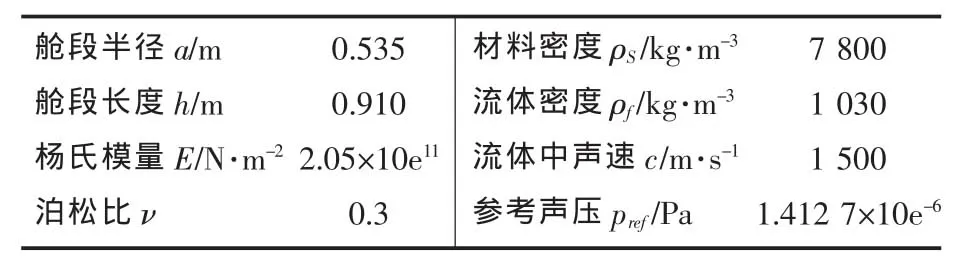
表1 舱段相关参数

本文计算舱段在100 N的激振力作用下舱段的辐射噪声，图2中表示了激振力的作用方向和位置。

在实际工程中，由于结构的复杂性，不仅对整艇建模需要耗费很长时间，而且由于其要划分的有限元网格数和节点数非常多，计算需要的时间也非常长，而且对计算机存储量的要求也非常高。在用大型计算机对整艇进行计算时，其单个频率流固耦合的计算时间就非常长，而如果能用舱段模型代替整艇模型进行计算，不仅建模能够节省很多时间，又由于其网格数和节点数大大减少，其计算单个频率的时间也会缩短非常多。

为了仅讨论潜艇舱段以外部分对舱段自身辐射声反射的影响，本文中舱段结构两端的舱壁被简支，并且构造了不同尺寸的反射面，反射面作为独立的刚性结构安置在舱段两侧。这样一来，能够剔除由于舱段结构振动向舱段以外其他部分传递而引起结构振动改变导致的辐射噪声差别，因此该反射面构造方法能够用于讨论单纯的反射对舱段辐射噪声的影响。实际建模中，反射面被简支约束，并且不与舱段结构直接相连，以此用来模拟完全刚性反射边界。

本文从模型复杂程度以及研究内容考虑，分别采用4种不同形式的反射面作为反射边界条件，这4种反射边界条件为：

情况A：舱壁两端加圆盘形反射壁，圆盘形反射壁距舱壁各为12 mm，如图4所示；

情况B：舱壁两端加大约一倍舱段长度的圆筒形反射结构，圆筒靠近舱壁一端开口，如图5所示；

情况C：去除整艇头尾舱结构比较复杂的部分，以圆形反射壁代替，如图6所示；

情况D：舱壁两端的反射结构为整艇头尾舱的外湿表面，如图7所示。

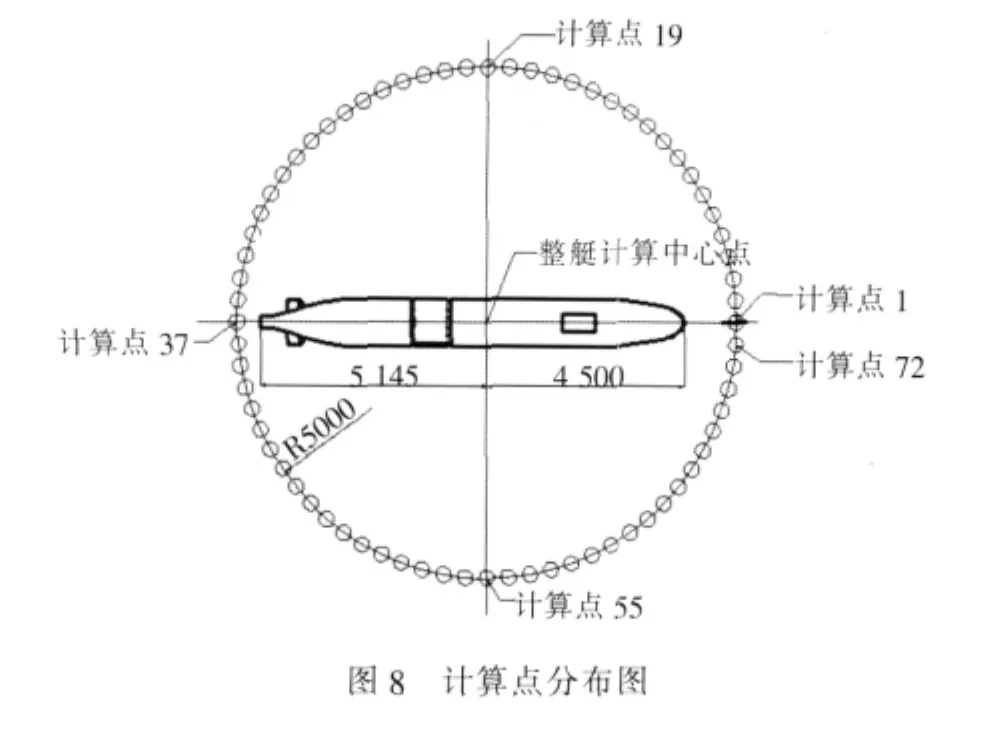
为了比较以上4种反射边界条件对辐射噪声的影响，本文计算了在以上4种反射边界情况下，潜艇结构在激振力作用下的辐射噪声。所计算舱段在水中的位置为：舱段中心线在水下5 m处。潜艇舱段辐射噪声计算点布置：为以整艇中心点（图7所示中心线交叉点）为圆点，半径为5 m的水平圆周上，每5°布置一个计算点，共72个计算点，计算点布置如图8所示。

对于舱段水下辐射噪声的数值计算，采用流体边界元耦合结构有限元的附加质量附加阻尼算法对4种反射边界情况下各计算点的舱段辐射噪声值进行数值计算。

3 附加质量阻尼算法

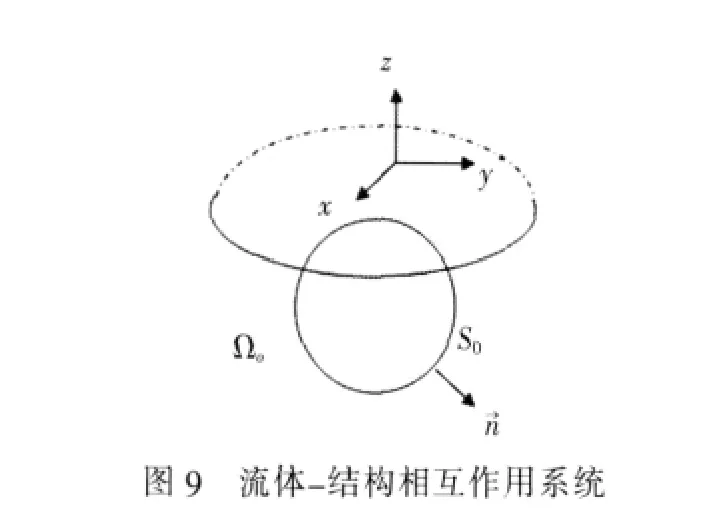
水下结构振动与辐射噪声问题是一个流体—结构相互作用的流固耦合问题。考虑如图9所示的结构—流体相互作用的系统：流体外域Ωo被弹

性薄壳结构S0分开。流体外域充满密度为ρo的声介质，其声速为co。若系统进入稳态，角频率为ω，则波数 ko＝ω2／co。

对流体外域，以声速度势φ为未知量的控制方程为：

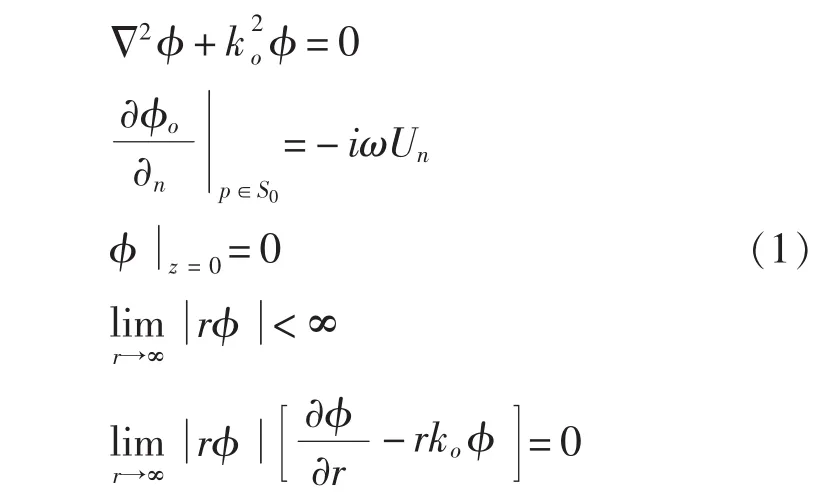
对结构域S0，采用通用的有限元离散步骤，并考虑到稳态响应问题，可以得到：

式中，KS为结构刚度矩阵；MS为结构质量矩阵；CS为结构阻尼矩阵；｛a｝为节点位移向量；｛f｝为直接作用在结构上的节点力；｛pout｝为外域流体对结构作用的等效节点力。

对流体外域，有单层势形式的边界积分方程：

式中，G（P，Q）为 Green函数，若不考虑自由面反射影响，则 G（P，Q）＝－eikor／4πr；若考虑自由面反射影响，则G（P，Q）＝－eikor／4πr －eikor1／4πr1）；σ（Q）为Q点的源强密度函数；

P（x，y，z）为外域中的场点；Q（ζ，η，ξ）为边界上的源点。

将边界离散为有限个三角形单元，并认为这些单元内物理量为常数，这样可将各单元物理量的平均值视作等于各单元形心处的值。若点P在边界单元形心上，则式（3）、式（4）可离散为代数方程组。

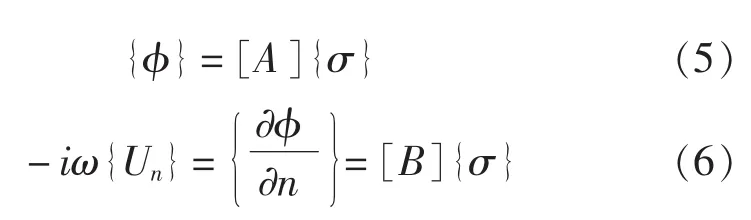
若已知边界上的法向位移，则声场中任意一点P处的速度势可计算为：

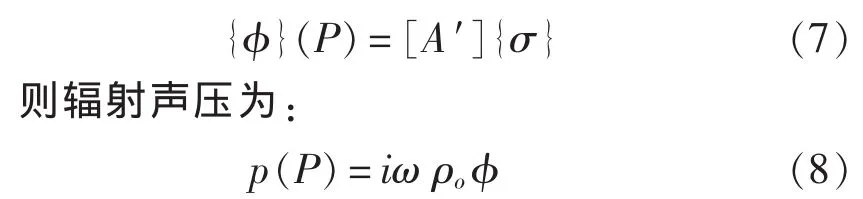
联立式（5）、式（6）可得到物面各单元平均速度势，则各单元平均压力向量为：

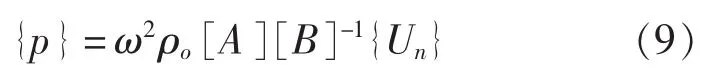
采用虚功等效原理，将外域流体作用于单元上的平均面压力等效为作用于结构节点上的节点力。

记单元上作用的流体压力为pt，单元节点具有虚位移｛δu（b）｝e，所引起的单元面上各点位移为，则该流体压力所作的虚功δ为：

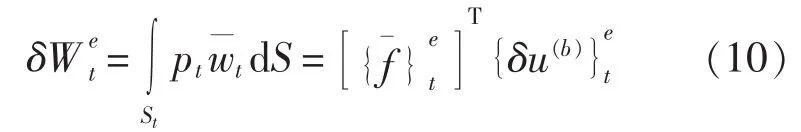
对所有流体－结构交接面单元进行这样的等效，并经过单元坐标向全局坐标的转换和组装，则整个等效过程可借助单元匹配矩阵［L］表示为：

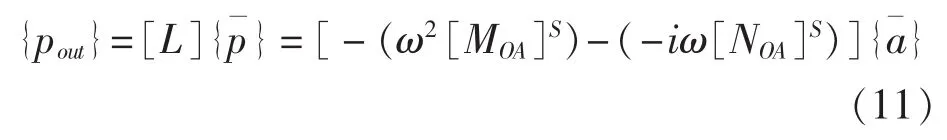
矩阵［MOA］S、［NOA］S即为外域流体对结构作用所产生的全局附加质量和附加阻尼矩阵。在NASTRAN软件程序中，可以通过FORTRAN和DMAP语言混合编程实现附加质量和附加阻尼矩阵的叠加［10，12］，这样，最终得到的结构—流体相互作用的动力方程为：

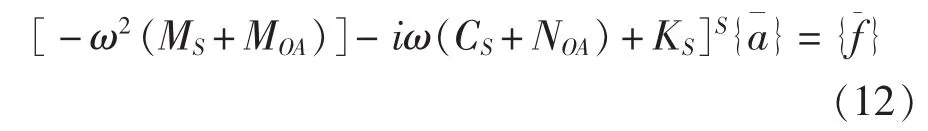
式（12）说明外域流体的耦合作用可以通过对结构质量矩阵和阻尼矩阵分别叠加外域流体的附加质量矩阵和附加阻尼矩阵加以考虑。

一旦得到结构位移，可提取结构－外域流体交接面上的节点位移，从而得到物面法向位移向量，并由式（8）计算声场中任意一点P处的声压速度势，获得声压。由式（9）可进一步计算流体－结构交接面上的声压，并进一步计算外域声场中任一点的辐射声压级。

4 网格划分与计算代价

采用三角形单元，对四种反射边界情况下的结构湿表面进行网格划分，划分情况如下：

情况A：结构湿表面划分为1 388个三角形网格，770个节点，如图10所示。其中舱段部分划分为676个三角形网格，370个节点，圆形反射壁结构划分为712个三角形网格，400个节点。

情况B：结构湿表面划分为2 404个三角形网格，1 268个节点，如图11所示，其中反射结构划分为1 728个三角形网格，898个节点。

情况C：结构湿表面划分为5 004个三角形网格，2 568个节点，如图12所示。其中反射结构划分为4 328个三角形网格，2 198个节点。

情况D：结构湿表面划分为7 882个三角形网格，4 007个节点，如图13所示。其中反射结构划分为7 206个三角形网格，3 637个节点。

由于流体附加质量和阻尼矩阵一般来说是满元的非对称矩阵［3］，所以对于水下舱段辐射噪声的计算，随着网格数和节点数的增加，所需计算时间和计算存储数据量也会急剧增加。由表2可以看出，结构越复杂，湿表面网格数和节点数就越多，这样无疑增加了计算的时间和数据存储量。例如情况D的网格数和节点数是情况A的5倍多，在计算频率较多的情况下，其计算代价将是非常大的。

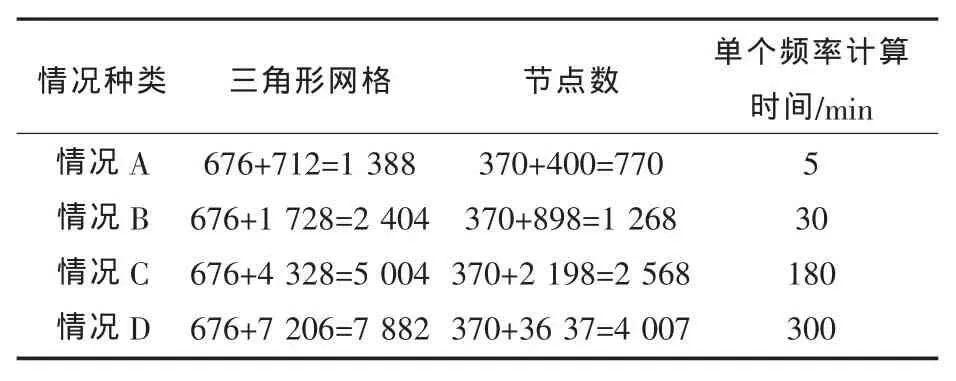
表2 不同情况湿表面网格划分和单个频率计算时间

5 数值计算及结果比较分析

本文计算了前述四种情况下舱段结构的辐射噪声频率特性，并将他们进行了对比。计算时，激振频率从50～1 000 Hz。

对于单个频率，比较4种情况下各计算点辐射声压级最大与最小值的差值。图14为200 Hz最大误差的分布图，图15为500 Hz最大误差分布图，从图上可以看出，4种情况在各计算点的最大误差随计算点位置不同和频率不同差别比较大。取各频率点最大误差的最大值，如图16为最大误差的最大值以频率为横坐标的分布图，由图可以看出，在200 Hz以下不同反射边界条件对舱段模型自身辐射噪声的影响不大，而在200 Hz以上，很多频率点的最大误差超过了3 dB，并且在个别频率点不同边界情况最大误差是非常大的，这可能是由于个别计算点出现极小值引起的。

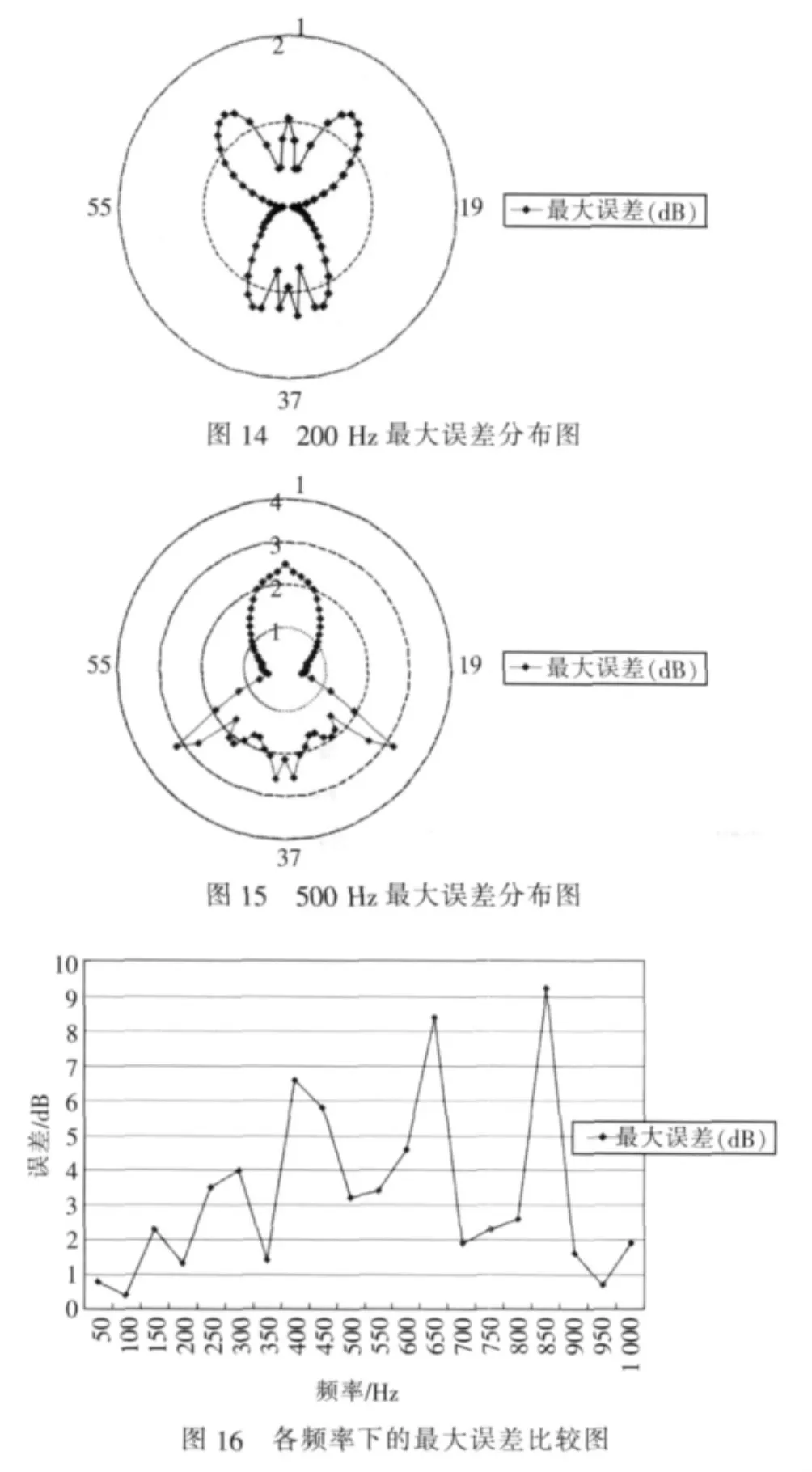
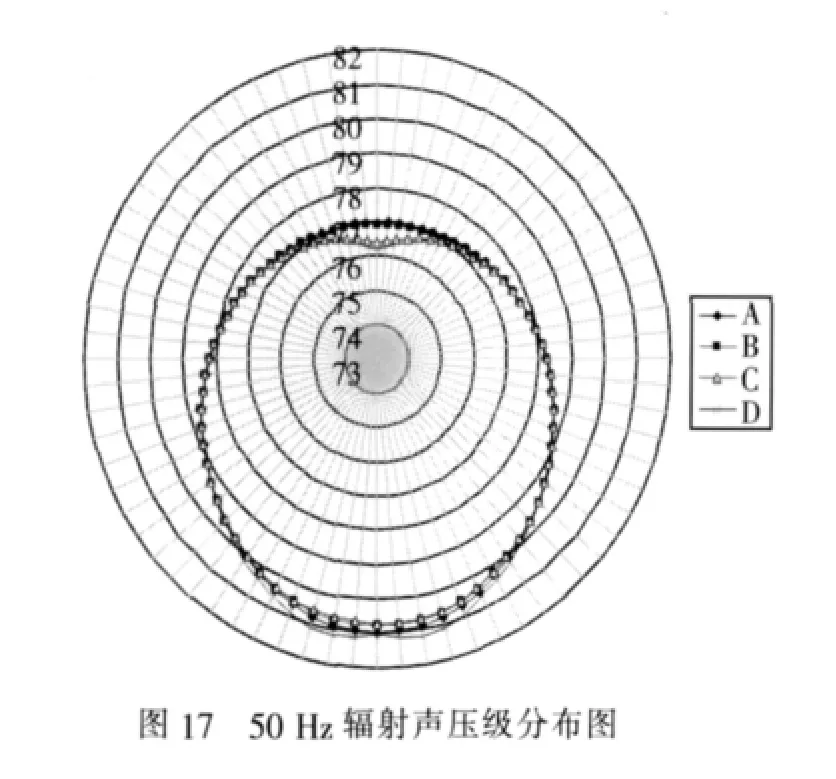
图17～图20为舱段结构在4种情况下单个频率的辐射声压级分布图，由图可以看出，虽然有些频率点辐射声压级的最大误差比较大，但舱段在各种情况下辐射噪声分布曲线比较吻合，其指向性比较一致。850 Hz辐射声压级的最大误差是最大的，但其辐射噪声的指向性仍然可以作为对舱段噪声辐射预报的参考。

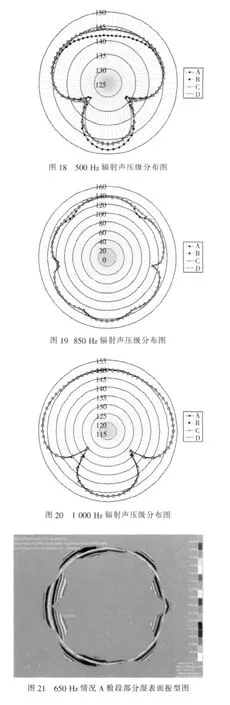
图21、图22为650 Hz情况A与情况D的舱段部分湿表面振型图，由图可看出，其振型基本相同。由此可以得出，从声反射的角度，辐射噪声的指向性可以作为对舱段噪声辐射预报的参考，但潜艇舱段以外其他部分声反射特性对舱段模型自身辐射噪声的影响不可以简单被忽略。

6 结束语

本文针对SUBOFF艇型潜艇模型的一个舱段进行了建模，计算该舱段在考虑不同声反射边界条件下的辐射噪声，并分析比较了他们的辐射效果，结果表明，不同声反射边界条件下舱段模型辐射噪声的指向性比较一致，但潜艇舱段以外其他部分壳体的反射边界对舱段自身辐射噪声的影响是不可以被简单忽略的。从声反射的角度看，对舱段的噪声辐射预报不可以简单忽略掉潜艇舱段以外的其他外壳部分声反射对舱段自身噪声辐射的影响。进一步有关变化规律的研究及有关振动传递的影响将在后续的研究中考虑。

［1］黄国权.有限元法基础及ANSYS应用［M］.北京：机械工业出版社，2004.

［2］谢志勇，周其斗，纪刚.双层柱壳的流固耦合模态计算与试验研究［J］.海军工程大学学报，2009，21（2）：97－101.

［3］曾娜，郭小刚.探讨流固耦合分析方法［J］.沈阳工程学院学报（自然科学版），2008，4（4）：382-386.

［4］GAUL L，WENZEL W.A coupled symmetric BE－FE method for acoustic fluid －structure interaction ［J］.Engineering Analysis with Boundary Elements，2002，26（7）：629－636.

［5］PADRON L A，AZNAREZ J J，MAESO O.BEM －FEM coupling model for the dynamic analysis of piles and pile groups［J］.Engineering Analysis with Boundary Elements，2007，31（6）：473－484.

［6］纪刚，张纬康，周其斗.随机力作用下的水下结构声辐射分析［J］.船舶力学，2006，10（2）：153－159.

［7］洪明，郭新毅，刘连海.含损伤加筋结构的振动与声辐射特性研究［J］.中国舰船研究，2007，2（6）：35－41.

［8］刘连海，洪明，郭新毅.含损伤加筋结构流固耦合动力特性与声辐射特性研究［J］.中国舰船研究，2007，2（2）：9－14.

［9］周其斗，张纬康.细长体在水中运动时的噪声辐射机理及预报方法［R］.国防科技预研基金项目研究报告，1997.

［10］ ZHOU Q，ZHANG W，JOSEPH P F.A new method for determining acoustic added mass and damping coefficient of fluid－structure interaction［C］//The Eighth International Symposium on Practical Design of Ships and Other Floating Structures，Elsevier，Amsterdam，2001：1185－1195.

［11］纪刚，张纬康，周其斗.静水压力作用的水下结构振动及声辐射［J］.中国造船，2006，47（3）：37－44.

［12］ ZHOU Q，JOSEPH P F.A numerical method for the calculation of dynamic response and acoustic radiation from an underwater structure ［J］.Journal of Sound and Vibration，2005，283（3/5）：853－873.

Approximate Method for Acoustic Radiated Noise Calculation of Sub Cabin Model in Replacing Full-Scale Model

Wang Lu－caiZhou Qi－dou Ji Gang Xie Zhi－yong Mo Deng－yuan
College of Naval Architecture and Power， Naval University of Engineering ，Wuhan 430033，China

The paper proposes an additional mass and damping approach combining Finite Element Method （FEM）with Boundary Element Method （BEM）to calculate underwater acoustic radiated noise from a submarine cabin of SUBOFF model taking into account different acoustic reflection boundary conditions.The comparison and analysis of the results show that using a cabin model of submarine replacing a full－scale model for noise estimation is feasible， and demonstrate an agreeable directivity of acoustic radiated noise under different acoustic reflection boundary conditions，while the error of maximal sound pressure level （SPL） are much bigger， thus the influence of acoustic reflection boundary conditions on the radiated noise of cabin model cannot be neglected.The research provides reference for noise estimation of different structures of submarine.

fluid-structural interaction； finite element method；boundary element method； radiated noise

U661.73

A

1673－3185（2010）06－26－07

10.3969/j.issn.1673-3185.2010.06.006

2010-01-23

王路才（1986－），男，硕士研究生。研究方向：舰艇声学与噪声控制。E-mail：wanglucai1＠163.com

周其斗（1962－），男，教授，博士生导师。研究方向：振动与噪声控制、水动力学。E-mail：qidou_zhou@126.com