钻地弹侵彻混凝土靶过程中弹体温度的变化*

张丁山,王 浩,冯国增,刘 赟,郭锦炎

(南京理工大学动力工程学院,江苏 南京210094)

1 引 言

实现深钻地是钻地武器追求的目标之一,也是确保有效摧毁深埋地下坚固目标的重要保证。对动能侵彻型战斗部,其钻地深度主要取决于战斗部的动能[1]。但在钻地弹侵彻混凝土靶实验中,随着着靶速度的提高,装载在钻地弹内部的炸药出现早燃早炸的现象明显增多。目前关于炸药发生早燃早炸现象有如下一种解释:钻地弹侵彻混凝土目标过程中发生高速滑动摩擦,而摩擦过程中所作的功90%以上将转变为热[2],导致钻地弹弹体表面温度升高,并由于钻地弹弹体材料导热性能良好,摩擦产生的热量通过热传导使弹体内部温度升高,威胁到战斗部装药的安全。因此,研究钻地弹侵彻混凝土靶过程中弹体温度的变化情况具有重要意义。目前对钻地弹侵彻性能的研究多集中于对钢靶的侵彻,而对混凝土靶的侵彻研究报道较少,对弹体温度变化情况的研究更少。本文中通过对弹体的传热分析,研究钻地弹侵彻混凝土靶过程中弹体温度的变化规律,分析影响弹体温度变化的主要因素。

2 钻地弹弹体温度变化计算

2.1 弹体闪温计算

动能钻地弹的侵彻部分主要由弹头段、战斗部圆柱段和弹尾(含引信)等部件组成,如图1 所示。

2.1.1 基本假设

计算钻地弹侵彻混凝土目标靶过程中由摩擦引起弹体闪温变化时,作如下假设和处理方法:

(1)消耗于滑动摩擦的机械功率全部转变为热,热流强度[2],其中μ为滑动摩擦因数,An为弹体与混凝土靶摩擦的表面积,p 为钻地弹侵彻过程中弹体受到的法向平均压强,v 为钻地弹的侵彻速度;

(2)热量只沿着弹体表面的法线向内部传导,而略去切向传热;

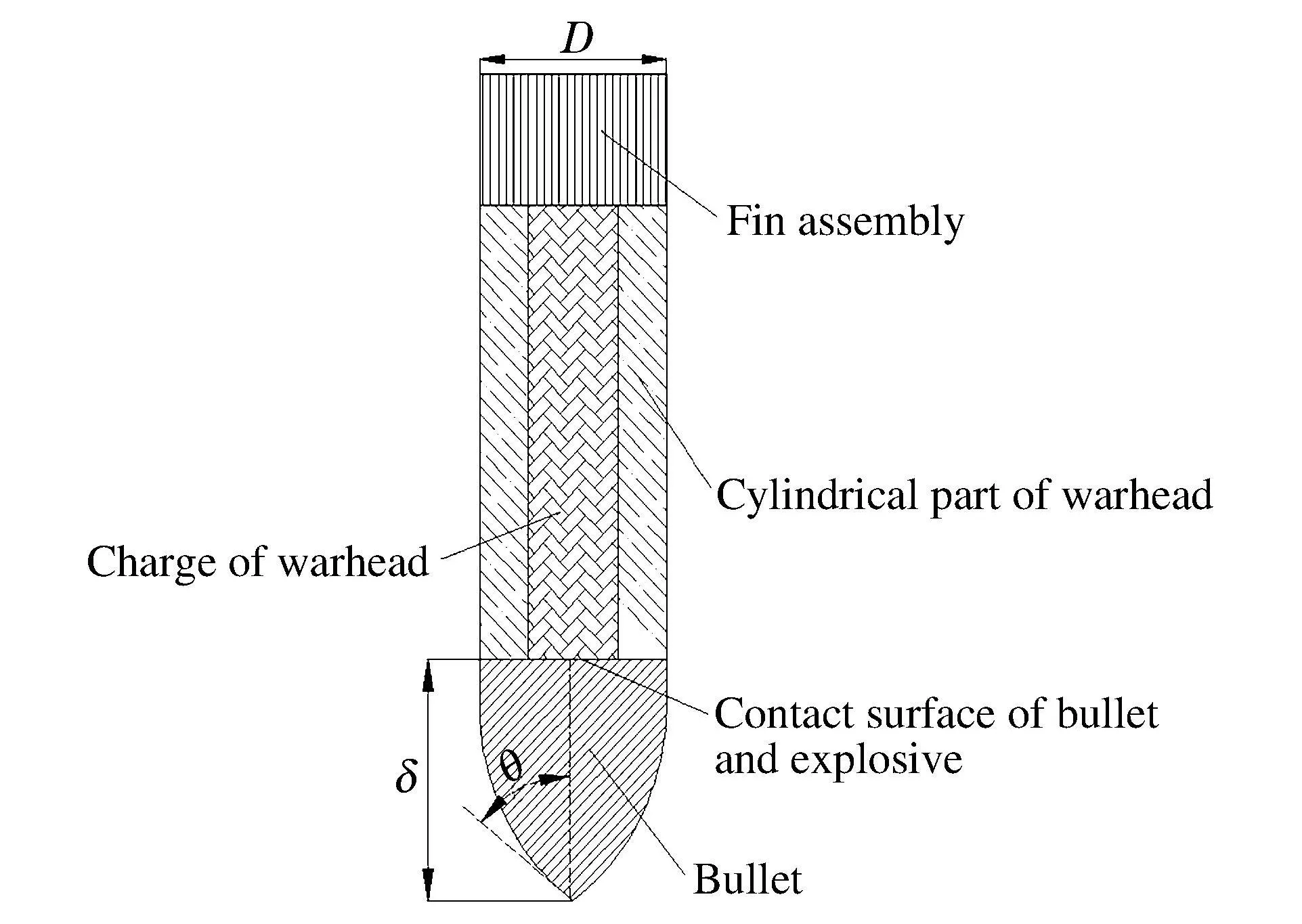
图1 钻地弹示意图Fig.1 The schematic drawing of earth penetrator

(3)侵彻过程中,钻地弹与目标靶间的摩擦主要发生在弹头部位,计算侵彻过程中弹体闪温变化时只计算弹头段的温度变化。

2.1.2 计算模型

弹体模型为:弹头半锥角为θ,弹体直径为D,弹头锥面近似分解为多个以D/(2sinθ)为高的等腰三角形。设有一热导率为k,边长为的“半无限长”三棱柱,垂直接触于密度为ρ、比热容为c、导温系数为a 的“半无限”固体的表面上,并且以速度v 作匀速直线运动,“半无限长”三棱柱与“半无限”固体的材料相同。根据假设(2),只分析“半无限”固体中短时受热的厚度为的“半无限”平板,并进一步将它简化为由无数个互不传热的垂直于表面的“半无限长”细杆组成。设供给平板的热流强度为Qk,对每个细杆顶端的平均供热时间为t,则由一维热传导方程

可解得弹体单位表面的最大温升(闪温)

由此计算出钻地弹侵彻过程中某一阶段由摩擦产生的最高闪温,此温度将持续0.01 ～1 ms[2]。

2.2 弹体温升计算

计算弹体温度变化时作如下假设:

(1)摩擦产生的热量全部储藏在弹体内而没有损失;

(2)弹体材料各物性参数为常数,不随温度变化而变化。

根据能量守恒可得

式中:m 为储藏摩擦所产生热量的弹体质量,c 为弹体材料比热容,ΔT 为温度变化值,F 为弹体所受摩擦力,h 为侵彻行程。

2.3 钻地弹弹体温度分布计算

计算钻地弹侵彻过程及侵彻结束后弹体温度变化时作如下假设:

(1)弹体表面温度以当时平均最高温度为主,即Tw;

(2)弹体内部与炸药接触面绝热;

(3)侵彻结束后,弹头段温度未达到平衡时不考虑弹头段的热量损失;

(4)钻地弹侵彻结束后弹体留在靶内。

此热传导问题的数学描述为

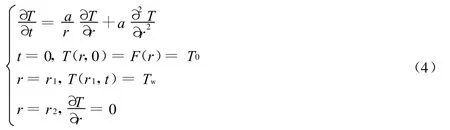
3 弹体温度数值计算

3.1 钻地弹的计算参数

以某一钻地弹为研究对象,计算分析钻地弹在侵彻混凝土靶过程中以及侵彻结束后一段时间内弹体温度变化情况,计算参数为:弹体直径80 mm,弹体壁厚15 mm,弹体长度800 mm,弹头半锥角30°,弹头长度与弹径比1.75,弹体材料35CrM nSi,初始侵彻速度800 m/s,混凝土靶强度30 MPa,弹体初始温度20 ℃,弹重30 kg。

3.2 钻地弹侵彻过程中闪温计算

钻地弹侵彻过程中摩擦力的计算公式[3]:

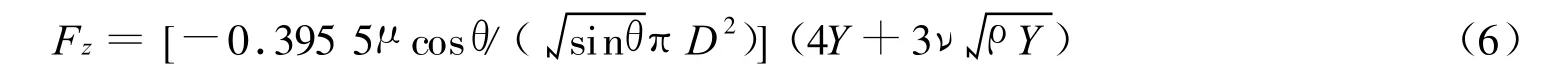
式中:Y 为混凝土类目标的极限抗压强度,Pa;ρ为混凝土类目标的密度,kg/m3;D 为弹丸的直径,m;θ为锥形弹半锥角,(°);μ为滑动摩擦因数。由式(6)可以得出

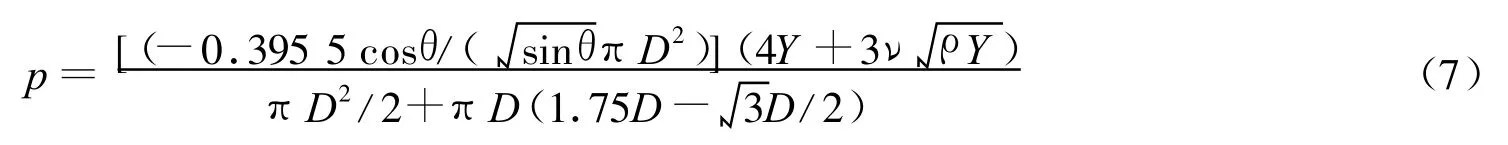
式中:p 为钻地弹侵彻过程中弹头受到的法向平均压强,Pa。

结合钻地弹侵彻混凝土计算公式[4],并应用式(2)可以计算得出钻地弹在侵彻过程中弹头由摩擦产生的最高闪温为6 968 K 左右,此温度持续的时间约为0.01 ms,整个摩擦过程即侵彻过程持续的时间为13 ms 左右。

3.3 侵彻过程弹体温度变化与分布

图2 为钻地弹侵彻混凝土过程中弹头段表面的温度变化情况。从图中可以得出:弹头表面温度变化大体可分为3 个阶段:初始阶段、闪温阶段和温度平缓上升阶段。初始阶段弹头表面温度为初始温度293 K;约0 ～6 ms 为闪温阶段,弹头表面由于高速摩擦将产生一系列的闪温,每一次闪温持续的时间约0.01 ms,此阶段闪温温度高于弹头的实际温度,弹头表面温度以闪温为主;约6 ～12 ms 为温度平缓上升阶段,此阶段闪温温度已低于弹头表面的实际温度,弹头表面温度以实际温度为主,表面温度随着摩擦的继续而平缓上升,此阶段到侵彻结束为止,侵彻结束时弹头表面温度为817 K 左右。

图3 为弹头段表面产生最高闪温瞬间时弹头段内部(相对表面而言)温度分布情况。从图中可以得出:表面产生最高闪温时影响区域很小,最高闪温影响区域为沿表面法线方向向里0.5 mm 左右的部分区间内。

图2 侵彻过程弹头段外表面温度变化曲线Fig.2 The temperature curve of the outer surface of shell head in the penet ration process

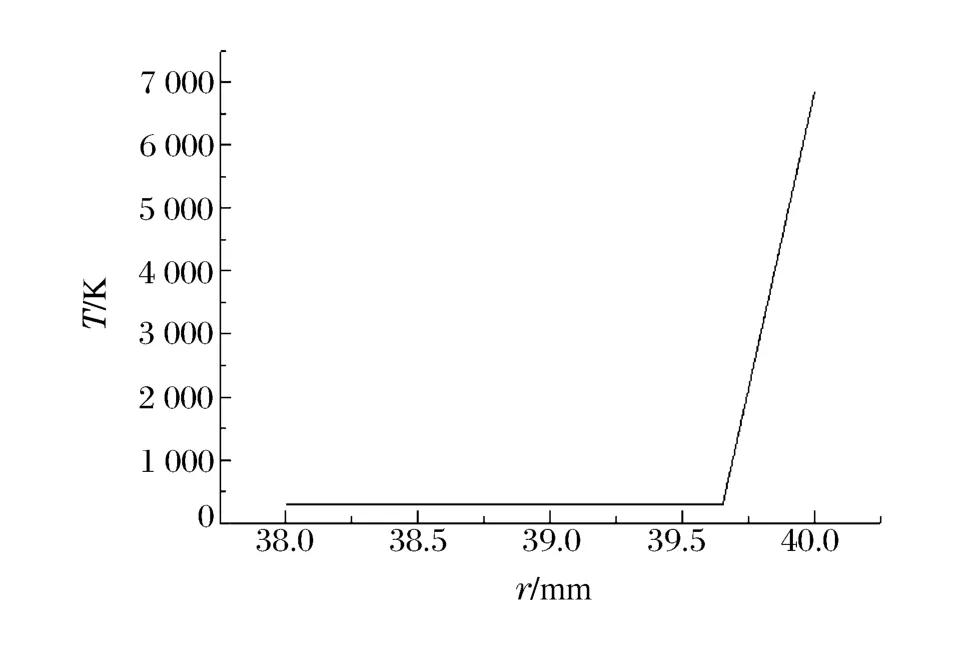
图3 最高瞬间闪温弹内分布曲线Fig.3 The temperature distribution curve of the maximum instantaneous flash inside shell body

图4 为侵彻过程弹头段内部温度变化曲线。其中温度曲线从上而下分别为沿弹头段表面法线方向向里距离d=0.5、1.0、2.5 mm 及d ＞2.5 mm 处的温度变化曲线(曲线重合即温度没有变化),图中T c为侵彻结束(v=0 时)后弹头与炸药接触面的温度。

图5(a)为侵彻过程中战斗部圆柱段外表面温度变化曲线。图5(b)为侵彻过程中战斗部圆柱段弹体内温度变化曲线(距表面1 mm处)。从图5(b)中可以得出侵彻过程中战斗部圆柱段壁厚大于1 mm处,其温度没有变化。

图4 侵彻过程弹头段内部温度变化曲线Fig.4 The temperature curve of the internal of shell head in the penetration process

图5 侵彻过程圆柱段外表面和弹体内温度变化曲线Fig.5 The temperature curve of the outer surface and internal of w arhead in the penetration process

3.4 侵彻结束后弹体温度变化与分布

图6 为侵彻结束后弹头段内部温度变化曲线。图中温度曲线从上而下分别为沿弹头段表面法线方向向里0、1、3、10、15、40 mm 处的温度变化曲线,从中可以得出弹头段温度平衡值为450 K 左右,即内表面最高温度为450 K。图中Tm 为弹体温度平衡时弹头与炸药接触面的温度。

图7 为侵彻结束后战斗部圆柱段弹体内温度变化曲线。图中温度曲线从上而下分别为沿战斗部圆柱段表面法线方向向里0、1、2、3、4、5 mm 处的温度变化曲线。从图7 中可以得出侵彻过程及其结束后战斗部圆柱段壁厚大于5 mm 处,其温度升高不会超过10 ℃。

图6 侵彻结束后弹头段内部温度变化曲线Fig.6 The temperature curve of the internal of shell head af ter the end of penetration

图7 侵彻结束后战斗部圆柱段弹体内温度变化曲线Fig.7 The temperature curve of the internal of w arhead after the end of penetration

3.5 弹头形状和弹丸着靶速度对弹头与炸药接触面温度变化的影响

在弹径一定的情况下,弹头形状(弹头段轴向厚度δ和弹头半锥角θ)和弹丸的着靶速度是影响弹头与炸药接触面最高温度的主要因素。表1 列出了着靶速度v=800 m/s 时不同弹头形状参数下侵彻结束(v=0 时)后弹头与炸药接触面的温度Tc和弹体温度平衡时弹头与炸药接触面的温度Tm。表2 列出了同一弹头形状参数(θ=30°,δ=120 mm)下不同着靶速度时侵彻结束(v=0 时)后弹头与炸药接触面的温度Tc和弹体温度平衡时弹头与炸药接触面的温度Tm。表1、2 中t 为侵彻时间;h 为侵彻深度。

表1 v=800 m/s 时弹头与炸药接触面温度Table 1 Temperature of the internal of shell head at v=800 m/s

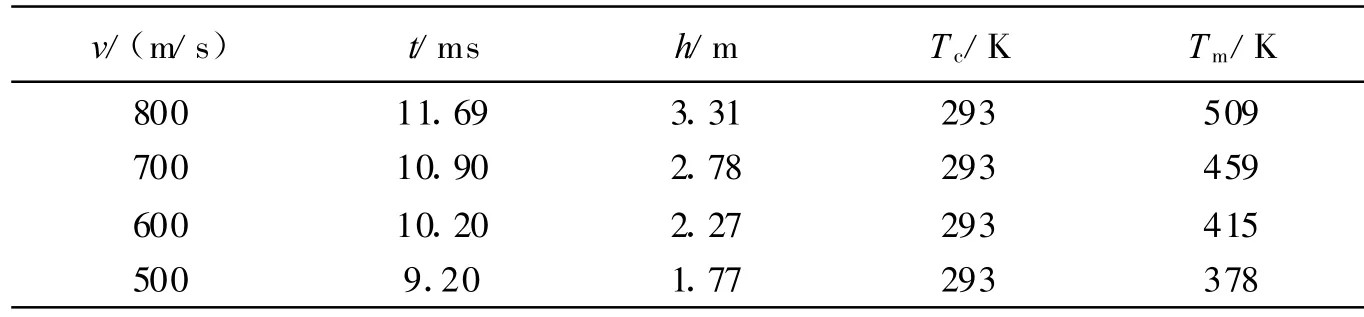
表2 θ=30°,δ=120 mm 时弹头与炸药接触面温度Table 2 Temperature of the internal of shell head at θ=30°,δ=120 mm

从表1 可以看出在着靶速度一定的情况下,弹头段必须具有一定的轴向厚度,否则在侵彻结束后,弹头段内部温度继续上升时,将会对战斗部装药构成威胁。同时对于不同的弹头半锥角必须设计不同的弹头段轴向厚度,当弹头半锥角较小时,在相同的着靶速度下,侵彻深度增加,摩擦作功量增大,所需弹头段轴向厚度增加。

从表2 可以看出,弹头段内部最高温度与着靶速度有直接的关系。在弹头形状一定的情况下,着靶速度越高,弹头段内部最高温度越大。

4 结果分析

依据钻地弹侵彻混凝土目标靶过程中弹体温度变化情况得出如下结论:

(1)钻地弹侵彻混凝土过程中,摩擦产生的弹体温升主要来自弹头段,但弹头与炸药接触面温升不高,战斗部圆柱段温度升高很小。弹丸侵彻结束留在混凝土目标靶中后,经过一段时间,弹头与炸药接触面温度会达到最大值。在本文计算中,弹丸侵彻结束留在混凝土目标靶中1 min 左右,弹头与炸药接触面温升达到150 ℃,战斗部圆柱段温升小于10 ℃。一般的炸药熔点高于200 ℃,弹头段与炸药接触面最高温度达到170 ℃左右,低于炸药熔点,且接触面上的炸药量不大于5 g,按炸药量为5 g 且温度为150 ℃持续500 min 计算,炸药热分解产生气体量约为0.5 mL,相对于战斗部装药剩余空间其量很小。由此可见不会对战斗部装药构成威胁。

(2)弹头形状(弹头段轴向厚度和弹头半锥角)、弹丸的着靶速度是影响弹头与炸药接触面温升的主要因素。着靶速度越大、弹头段轴向厚度越小,最终温度越高;如果弹头段轴向厚度小于某一特定值,弹头与炸药接触面最高温度将接近甚至达到战斗部装药的熔点,会对战斗部装药的安全构成威胁。例如本文计算中v=800 m/s、θ=30°、δ=120 mm 时弹头与炸药接触面温度最高可达509 K,而v=800 m/s、θ=15°、δ=200 mm 时弹头与炸药接触面温度最高可达622 K,都超过炸药的安全范围。

5 结束语

计算求解了钻地弹侵彻混凝土目标靶过程弹体温度变化情况,得出弹体温度变化最显著部位为弹头段,并得出如果侵彻结束后钻地弹留在混凝土靶中,一段时间后弹头与炸药接触面的温度将达到最大值,有可能对战斗部装药构成威胁的结论。同时分析了不同着靶速度和不同弹头形状对弹头与炸药接触面最高温度的影响,得出对应一定着靶速度下弹头段轴向厚度的安全范围。如要获得钻地弹侵彻混凝土靶时弹体的详细温度场变化情况,可以结合钻地弹侵彻混凝土的机理研究、能量转换以及高速摩擦特性进行更深入的研究。

[1] 王浩,陶如意.截卵形弹头对混凝土靶侵彻性能的试验研究[J].爆炸与冲击,2005,25(2):171-175.WANG Hao, TAO Ru-yi.Experimental study on the penetration performance of truncated-ogive nose projectile[J].Explosion and Shock Waves, 2005,25(2):171-175.

[2] 戴振东,王珉,薛群基.摩擦体系热力学引论[M].北京:国防工业出版社,2002:52-68.

[3] 程义,杨清文,吴硕.助推钻地弹侵彻混凝土靶研究[J].弹道学报,2006,18(2):72-74.CH ENG Yi, YANG Qing-wen,WU Shuo.Penetrating concrete targets of earth penetrating w eapon w ith boosting[J].Journal of Ballistics, 2006,18(2):72-74.

[4] 文鹤鸣.混凝土靶板冲击响应的经验公式[J].爆炸与冲击,2003,23(3):267-273.WEN H e-ming.Em pirical equations for the impact response of concrete targets[J].Explosion and Shock Waves,2003,23(3):267-273.