新型头形弹体对混凝土的侵彻*
孙传杰,卢永刚,张方举,李会敏
(中国工程物理研究院总体工程研究所, 四川 绵阳621900)
1 引 言
为提高弹体侵彻性能,学者们开展了许多工作。J.R.Mayersak[1]提出了一种较新颖的侵彻研究思路,设想在常规卵形头形弹体头部加装一小圆柱形成新型头形弹体,使得新型头形弹体在侵彻过程中产生类似“超空泡效应”现象,减小弹体的侵彻阻力,以大幅度提高弹体侵彻性能。J.R.M ayersak 通过开展对水、沙介质的侵彻实验基本印证了他的设想。但对于与水、沙目标特性差异很大的混凝土、岩石等坚固介质是否具有类似侵彻效应,J.R.Mayersak 却未开展相应的研究工作。
本文中借鉴J.R.Mayersak 的研究思路,对强度为9.0、28.4 MPa 的混凝土靶开展新型头形弹体的侵彻实验,观察新型头形弹体侵彻混凝土靶的侵彻效应,探索新型头形弹体的侵彻性能和侵彻机理。在此基础上,提出混凝土强度弱化量纲一因子S2 和头部小圆柱侵彻开孔半径bt,并基于空腔膨胀理论初步建立新型头形弹体侵彻混凝土介质的理论分析模型。最后初步探讨提高新型头形弹体侵彻性能的2个途径:在侵彻过程中实现S2 的减小和bt 的增大。
2 侵彻实验
2.1 实验弹及靶体状态
实验弹编号分别为弹A、弹B1、弹C2 和弹C3,其外形如图1 所示,结构参数如表1 所示,表中Dn和L n 分别为头部小圆柱体的直径和长度,L p 和Dp分别为弹体长度和直径,ψ为曲径比,m 为质量。各实验弹的弹径相同,质量基本相等,弹材均为D6A高强度钢。
实验靶体为素混凝土靶,侧表面用铁皮箍紧。靶体分为A 靶和B 靶,A 靶的尺寸为Ø500 mm×1 500 mm,平均轴心抗压强度实测值为9.0 M Pa;B靶的尺寸为Ø500 mm×700 mm,平均轴心抗压强度实测值为28.4 M Pa。2 种靶体中的卵石直径均不大于6 mm。

图1 实验弹外形图Fig.1 Photographs of projectiles
2.2 实验方法
采用Ø25 mm 火炮作为加载平台开展正侵彻实验,侵彻速度约300、800 m/s,通过靶网测试弹体着靶速度,利用高速摄像机记录弹体的着靶姿态。
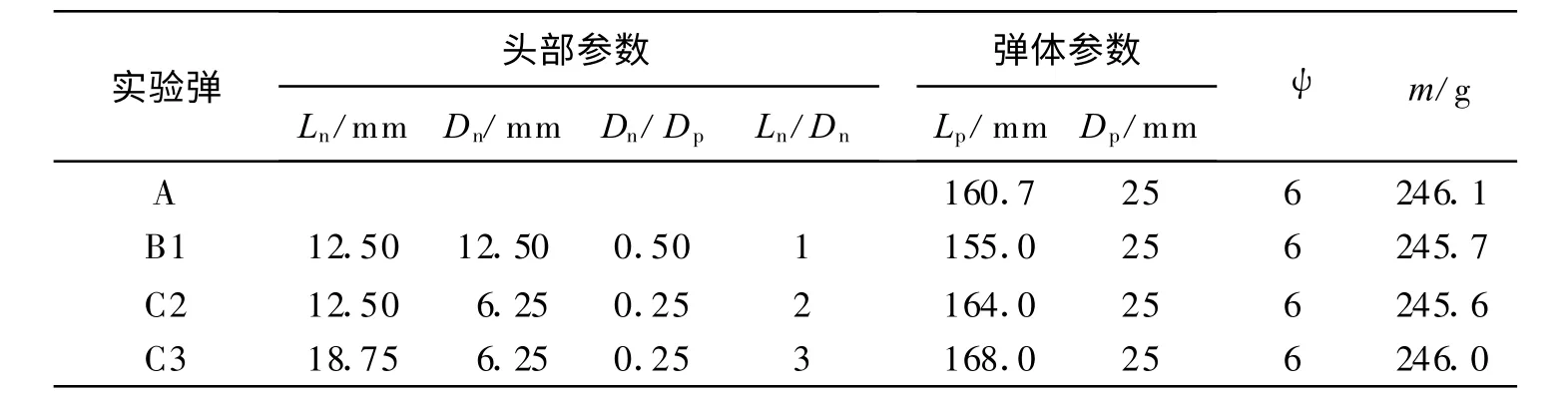
表1 实验弹参数Table 1 Characteristic parameters of projectiles
2.3 实验结果及初步分析
2.3.1 隧道开孔
实验观测发现,不同头形弹体以不同速度侵彻不同强度靶体获得的隧道开孔孔径无明显差异,与弹径相当。对新型头形弹体侵彻后的靶体进行解剖均未观测到有隧道开孔扩大现象。
2.3.2 侵彻深度
实验弹侵彻深度数据如表2 所示,表中f c 为靶体抗压强度,v 为撞击速度,h 为侵彻深度。不同头形弹体撞击速度-侵深对比如图2 所示。
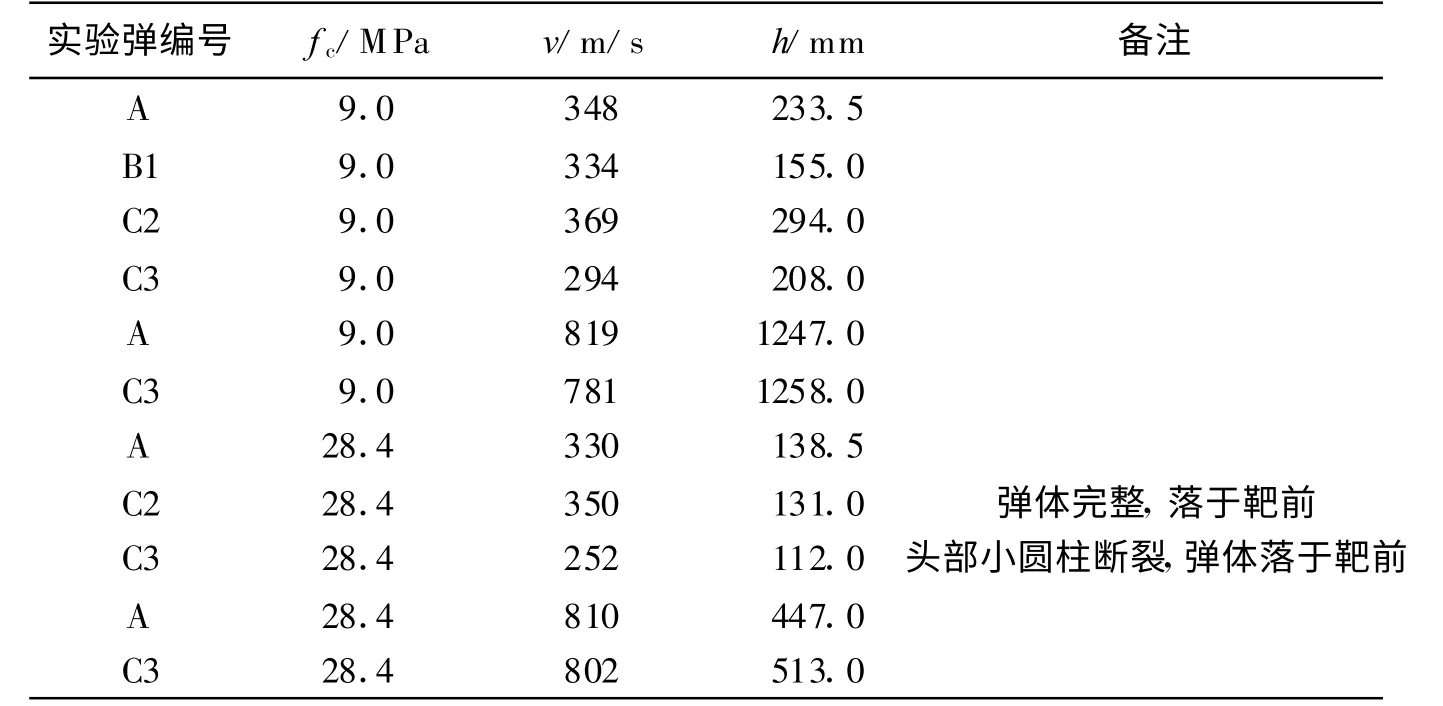
表2 侵彻深度实验数据Table 2 Penetration data of projectiles

图2 撞击速度与侵深的关系Fig.2 Relationship between impact velocity and penetration depth
2.3.3 新型头形弹体侵彻机理初步分析
由图2 可初步发现,新型头形弹体的头部参数在一定范围时,其侵彻性能可优于常规头形弹体的侵彻性能,并且新型头形弹体的侵彻性能与其头部小圆柱的直径和长度有一定关系。
此外,通过观测回收弹体及靶体解剖,初步认为新型头形弹体的侵彻机理为:头部小圆柱对目标介质进行先期侵彻,造成弹体侵彻路径周围介质一定程度的强度弱化,有可能降低弹体总的侵彻阻力。
3 模型建立
3.1 假设条件
基本假设包括:
(1)弹体弧形头部形状为正切卵形;
(2)采用刚性假设,弹体在侵彻过程中无变形、无质量侵蚀,且忽略弹体摩擦力;
(3)弹体头部小圆柱平头所受法向应力仍采用空腔膨胀理论计算其所受应力[3];
(4)弹体头部小圆柱先行侵彻混凝土,并对混凝土造成一定强度弱化。
3.2 新型头形弹体侵彻过程及相关参数定义
图3 为新型头形弹体侵彻混凝土的几个典型阶段,其中(a)~(c)分别为新型头形弹体头部小圆柱侵彻阶段、新型头形弹体头部卵形部分侵入阶段和新型头形弹体头部完全侵入阶段。
理论模型涉及的主要参数定义如下:L1为头部小圆柱长度;L2为头部卵形部分长度;L 为头部长度;a 为弹体半径;b 为小圆柱半径;s 为卵形部分圆半径;bt 为小圆柱开孔半径;φ1 为头部圆弧段与混凝土接触处的圆心角;φ0 为头部圆弧段与小圆柱连接处的圆心角;ψ为圆弧段曲径比,ψ=s/(2a);q 为小圆柱半径与弹体半径之比,q=b/a;R 为小圆柱开孔半径与弹体半径之比,R=bt/a;S、S1、S2、Sn为混凝土强度量纲一因子,且S 1=S。
根据图4 可推导如下协调关系式
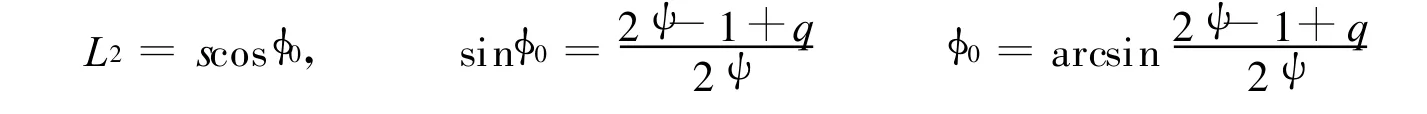
且
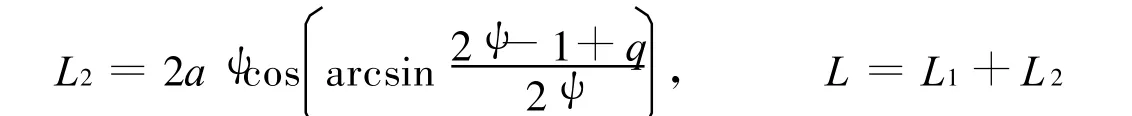

图3 新型头形弹体侵彻过程Fig.3 Process of cylindrical-nose-tip projectiles penetrating into concrete

图4 参数定义Fig.4 Parameter definition
3.3 侵彻过程及理论模型建立
以弹体与混凝土接触初始位置为坐标原点,弹体侵彻方向为x 坐标正方向。
3.3.1 第1 阶段(小圆柱头部侵彻阶段)
该阶段仅新型头形弹体头部小圆柱平头受力,头部卵形部分还未与混凝土接触。该阶段的初始和终了条件为:0 ≤x ≤L1,0 ≤t ≤t1,v1≤v ≤v0。
根据空腔膨胀理论,弹体侵彻表面的法向应力为

式中:A=S f c,S=82.6(f c/106)-0.544,f c 为混凝土抗压强度,MPa;B=ρt,ρt 为混凝土密度。
此阶段仅头部小圆柱平头受力(忽略摩檫力),则弹体轴向受力为

式中:α0=πb2A,β0=πb2B。
根据牛顿第二定律mdv/dt=-F0,可求解得到第1 阶段的位移、速度和加速度的表达式

第1 阶段结束后,
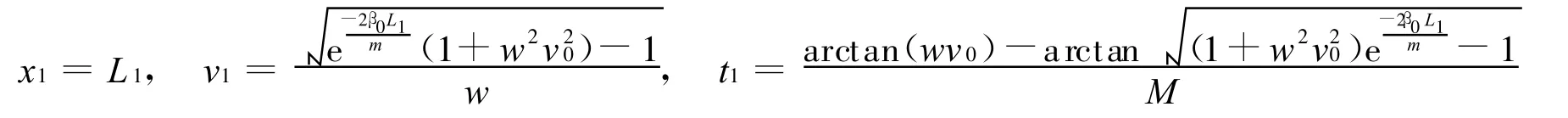
3.3.2 第2 阶段(头部小圆柱完全侵入,卵形头部侵彻阶段)
该阶段新型头形弹体头部小圆柱完全侵入,而头部卵形部分开始侵入混凝土。假设卵形弧段侵入过程所受轴向力随位移线性变化。为便于获得解析解,假设小圆柱平头所受轴向力为常量,并等于第1阶段结束时小圆柱平头的轴向力。该阶段的初始和终了条件为:L1≤x ≤L,t1≤t ≤t2,v2≤v ≤v1。
该阶段弹体的受力为
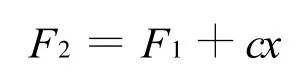
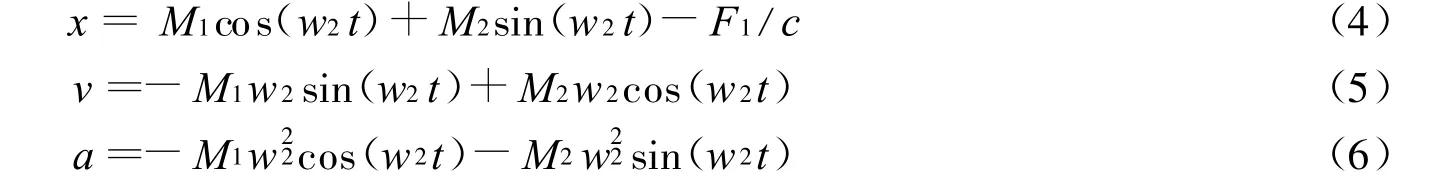
式中:
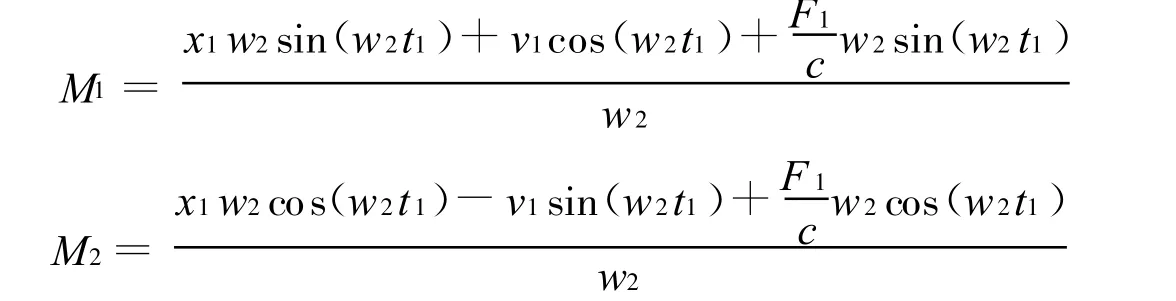
第2 阶段结束后,
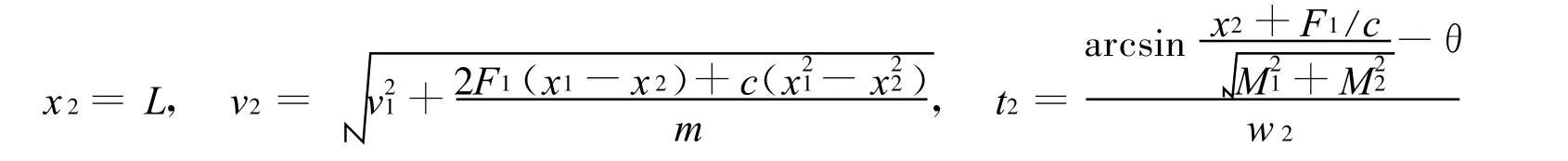
3.3.3 第3 阶段(新型头形弹体头部完全侵入阶段)
该阶段新型头形弹体头部完全侵入混凝土。假设小圆柱平头先行侵彻形成的开孔半径为bt,则卵形弧段所受轴向力的起始积分点处的圆心角为(而非),此外考虑小圆柱平头先行侵彻对混凝土产生一定强度弱化。该阶段的初始和终了条件为:x ≥L,t ≥t2,0 ≤v ≤v2。
小圆柱平头受力为

卵形弧段受力为

则该阶段弹体的受力为
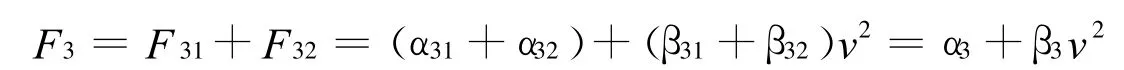

根据第2、3 阶段的速度和受力连续性关系可求得第2 阶段中的常数

至此推导获得了新型头形弹体侵彻混凝土的理论模型。
4 理论预测与实验结果的对比
根据对解剖靶体的观测,分析认为新型头形弹体的侵彻过程无开孔扩大效应,因此小圆柱开孔半径bt 等于小圆柱半径b。
文献[4]中根据实验结果拟合了侵彻次数与混凝土强度弱化量纲一因子的关系

式中:S1、Sn 分别为第1、n 次侵彻对应的混凝土强度量纲一因子,即S 1=S。由式(10)得到混凝土强度弱化量纲一因子S2=0.690 5S1。但由于式(10)仅是实验数据的拟合,需谨慎外推。本文中采用最小二乘法对本次实验数据进行拟合,以获得混凝土强度弱化量纲一因子S2。
拟合实验弹C3 对9.0、28.4 MPa 混凝土靶的侵彻实验数据分别得到S2=0.23S1 和S 2=0.64S1。由于受侵彻数据所限,因此下面理论分析时暂假设其他不同头形参数的新型头形弹体在侵彻过程中对相同抗压强度的混凝土的强度弱化规律相同。
图5、图6 为理论预测的速度-侵深和实验数据的对比。由图6 可见,对于28.4 M Pa 的混凝土,实验弹A 和实验弹C3 的理论预测值与实验数据在低速段和高速段符合程度均较好。对于实验弹C2,在低速段其理论预估值与实验数据的符合程度也非常良好。
对于9.0 M Pa 的混凝土,实验弹A 的理论预测值在高速段偏低。实验弹C3 的理论预测值则与实验数据符合较好。实验弹B1 和C2 的理论预测值在低速段与实验值较接近,由于无高速段实验数据,因此在高速段理论预估与实验的符合程度暂无法比较。
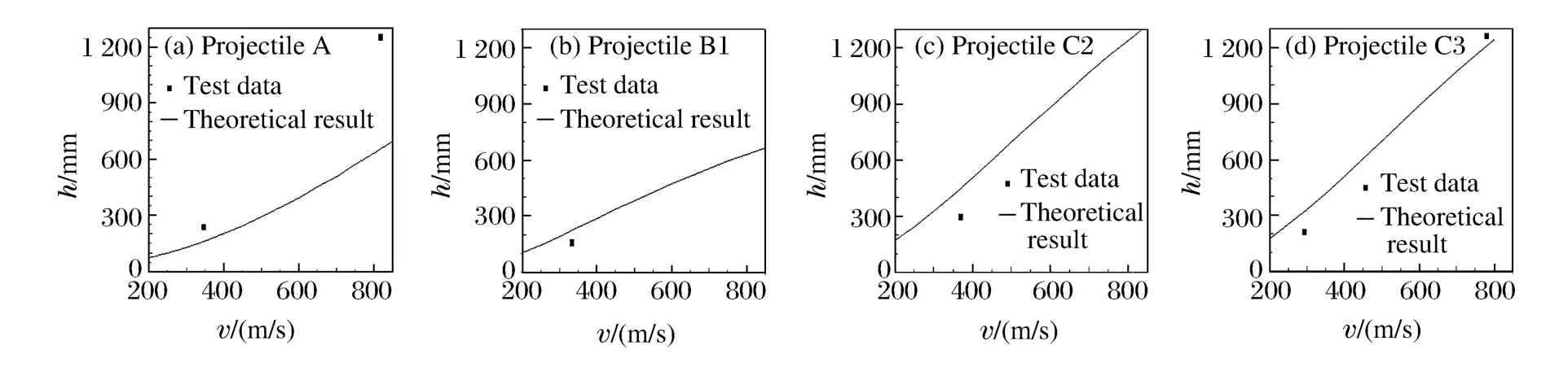
图5 不同头形实验弹撞击速度-侵深关系(9.0 MPa 混凝土)Fig.5 Impact velocity vs penetration depth for the projectiles into concrete targets with the st rength of 9.0 MPa

图6 不同头形实验弹撞击速度-侵深关系(28.4 M Pa 混凝土)Fig.6 Impact velocity vs penetration depth for the projectiles into concrete targets with the strength of 28.4 MPa
通过上述比较分析,可初步获得以下认识:(1)对于28.4 M Pa 混凝土,理论预测结果与实验数据符合程度良好,可定性反映不同头形弹体的侵彻规律;(2)对于9.0 M Pa 混凝土,理论预测结果与实验数据对不同头形弹体的符合程度出现一定的分散性(低速段和高段难以调和),但仍可基本定量反映不同头形弹体的侵彻规律。
5 讨 论
下面以新型头形弹体C3 侵彻28.4 M Pa 混凝土为例,初步讨论混凝土强度弱化量纲一因子S2 和小圆柱开孔半径bt 对新型头形弹体侵彻性能的影响。
图7(a)为在小圆柱开孔半径bt等于小圆柱半径b 时,不同混凝土强度弱化量纲一因子S2条件下新型头形弹体的侵彻性能对比。由图可见,随着S2/S1 的减小,弹体侵彻阻力随之降低,而弹体的侵彻性能则相应获得提高。图7(b)为不考虑混凝土强度弱化时,不同小圆柱开孔半径bt 条件下新型头形弹体的侵彻性能对比。由图可见,随着头部小圆柱开孔直径的增大,弹体与混凝土介质的接触面积相应减小,弹体所受阻力降低,当开孔直径等于弹径时,弹体仅头部小圆柱与介质接触,弹体的侵彻性能将获得大幅度提升,这即是文献[1]所预期的最理想的侵彻方式。
因此,在侵彻过程中实现S 2 的减小和bt 的增大是提高新型头形弹体性能的2 个主要途径。

图7 不同S2 和bt 时C3 的撞击速度-侵深关系图Fig.7 Im pact velocity vs penetration depth of projectile C3 into concrete in the case of S2 and bt
6 结束语
在实验研究的基础上,初步分析了新型头形弹体的侵彻过程和侵彻机理,提出了混凝土强度弱化量纲一因子S2和头部小圆柱侵彻开孔半径bt,并基于空腔膨胀理论初步建立了新型头形弹体侵彻混凝土介质的理论分析模型。结果表明,对28.4 MPa 混凝土,理论预测结果与实验数据具有较好的一致性。对9.0 M Pa 混凝土,理论预测结果与实验数据有一定偏差,但仍可基本反映新型头形弹体的侵彻规律。
此外,还初步探讨了提高新型头形弹体侵彻性能的2 个途径,即在侵彻过程中实现S2 的减小和bt的增大。
与陈小伟博士进行了很多有益的讨论,在此表示感谢。
[1] Mayersak J R.Kinetic energy cavity penetrator weapon[P]:US,US2004/0231552[R].2004-11-25.http:∥w w w.freepatentsonline.com/
[2] Forretal M J, Frew D J, Hanchak SJ,et al.Penetration of grout and concrete targets w ith ogive-nose steel projectiles[J].International Journal of Impact Engineering, 1996,18(5):465-476.
[3] Teland J A,Sjol H.Penetration into concrete by truncated projectiles[J].International Journal of Impact Engineering, 2004,30(4):447-464.
[4] Gomez J T, Shukla A.Multiple impact penetration of semi-infinite concrte[J].International Journal of Impact Engineering,2001,25(10):965-979.

