基于有限元法的玻璃啤酒瓶应力分析
樊爱珍
(陕西工业职业技术学院基础部, 陕西 西安 712000)
0 引言
从目前国内啤酒生产厂家来看,采用玻璃瓶装的占绝大多数(超过95%).玻璃瓶作为周转瓶能够多次使用,而且玻璃容器各种各样的形状、大小和颜色对用户都颇具吸引力.
啤酒瓶是受压容器,为易碎品,在啤酒瓶包装车间的洗瓶、压盖和杀菌等工序中容易炸裂,此外在销售和消费过程中也经常发生炸裂.啤酒瓶爆炸的原因很多,其根本原因在于啤酒瓶强度不够.啤酒瓶内由于二氧化碳气体的存在,常保持着内压,温度升高则内压上升.因此,研究罐装啤酒瓶在内压力作用下的应力分布,改进其造型结构,增加其强度,对于提高啤酒瓶的使用寿命,避免啤酒瓶的突然爆炸,进而控制啤酒瓶的数量,减少环境污染具有重要的社会意义,又有其潜在的经济价值.
啤酒瓶按瓶型式分有溜肩和端肩两种,按容量分为355 mL和640 mL,本文就此两种瓶型进行了分析.
有限元分析是将机械结构系统转化成由节点及元素所组合的有限元模型,该有限元模型与机械结构系统的几何外形一致.有限元模型的建立是将结构转换成许多节点和元素相连接,通过点、线、面、体积,先建立结构系统的几何外形,再通过360度的旋转得到实体模型.ANSYS作为一个成功的有限元分析软件,在机械、电机、土木、电子以及航空领域得到了广泛的应用.在机械结构分析方面,从静力分析、模态分析、谐振响应分析、瞬态动力分析到结构疲劳分析都可以非常好地完成[1-3].
1 建立啤酒瓶的有限元模型与求解
1.1 几何模型的建立
通过精确测量啤酒瓶的外形尺寸,结合啤酒瓶的设计规范和理论得到其原始几何尺寸.当节点建立完成后,必须使用适当的元素,将结构按照节点连接成元素,进而建立有限元模型(如图1、图2所示).

图1 溜肩瓶节点的建立 图2 端肩瓶节点的建立
1.2 有限元模型的求解
有限元法的思想是“化整为零,集零为整”,它将模型划分成连续的单元网格, 单元之间通过节点连接, 单元内部的待求量可由节点之间通过选定的函数关系插值求得,简单的单元形状易于由平衡关系或能量关系建立节点之间的方程,给定边界条件便可求解.单元划分越细,计算结果越精确.

图3 溜肩瓶模型的建立 图4 端肩瓶模型的建立
本文将两个几何模型在ANSYS中网格化生成有限元模型,大约生成几万个单元.为了计算的方便, 利用其轴对称性, 本文取其四分之一模型进行分析, 约束瓶口端面Y方向的移动,约束对称面上的相对移动,从而得到模型的约束条件(如图3、图4所示).
根据文献[4]、[5],罐装啤酒瓶的内压主要是由含二氧化碳的液体引起的,而跟液体的重力产生的压力无关.本文对640 mL溜肩瓶用0.5 MPa压力作用于瓶体内表面,对355 mL端肩瓶用0.4 MPa压力作用于内表面,用来模拟实际的罐装内压[6],在计算机上进行分析之后可以得到其应力分布图.
本文采用的玻璃材料物理参数为:杨氏模量E= 67.7 GPa,泊松比μ=0.24.

表1 应力最大值分布列表(溜肩瓶)

表2 应力最大值分布列表(端肩瓶)
由计算结果(表1、表2)可以看出,溜肩瓶在瓶口和瓶颈处的应力分布值较小,肩瓶处开始变大,到了瓶身处应力变得很大,而在瓶底的过渡处应力分布较小.在这个连续变化中,瓶的内表面比外表面的应力分布要大,在瓶底的内表面中心处应力达到了最大值,而在瓶底与瓶身的过渡处的内表面应力分布也是很大的(如图5所示).
作为比较,我们从端肩瓶可以看出,应力分布值在瓶口、瓶肩和瓶身的过渡处、瓶身和瓶底的过渡处是比较小的,而在瓶身以及瓶肩和瓶颈的过渡处分布着较大的应力值(如图6所示).
2 分析与优化
2.1 计算结果的分析
(1)由图5、图6的应力分布图可以看出,两种瓶型的应力最大点都在瓶底的中心点.对于溜肩瓶而言,较大的应力分布区在瓶身,这完全是由内压力产生的应力分布.根据文献及网上的报道,由内压引起的破损或者爆炸产生的放射状裂纹比较多,而且压力越高裂纹越多,破损的区域集中在瓶身处.因为瓶底的厚度比瓶身大,强度较大,而且瓶底产生的应力主要是压应力,瓶身的应力是拉应力,所以破损主要集中在瓶身,这和文献的结论是一致的[7-9].对于端肩瓶而言,应力的集中区域在瓶底和瓶肩处.比较端肩瓶和溜肩瓶可以看出,瓶颈与瓶身的过渡越光滑,曲率半径越大,在瓶肩处产生的应力集中就越小,因而改善瓶身和瓶肩的结构,加强其强度对防止啤酒瓶的爆炸是非常有必要的.
(2)由表1、表2可见,端肩瓶的应力最大值在10 MPa左右,溜肩瓶的最大应力在4 MPa左右,可见溜肩瓶比端肩瓶的应力最大值要小一些.
2.2 优化设计
为了克服溜肩瓶较大应力分布在瓶身的缺点,本文在溜肩瓶的瓶身外表面加了两道环形凸带(如图7、图8所示).经求解表明,其瓶身应力分布值普遍减小了,整个瓶体的应力分布更均匀,在瓶体外表面应力的减小值是很显著的,在内表面应力的分布也更加连续,相对值差别变小了,应力最大处也由瓶底中部移到瓶底与瓶身的连接处.加强环利于贴标签,其造型与实现也非常容易,所以无论从理论上还是从实际的工艺生产上来说,这都是比较好的强度提高措施.环形加强环能够在啤酒瓶相互撞击时产生缓冲作用,这对防止啤酒瓶的相互冲击产生的破损尤其有非常显著的效果.
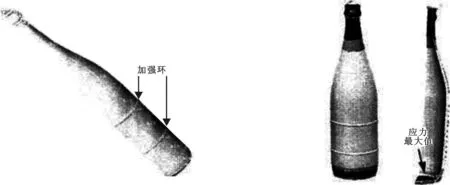
图7 结构优化模型 图8 优化后应力的分布
对于玻璃材料,其抗拉许用应力远远小于抗压许用应力,前者大约是后者的十分之一左右,所以研究玻璃瓶的强度问题只要考虑其拉应力的分布即可.玻璃破损时,通常是从玻璃表面上的伤痕开始破裂的,这称为破坏起点.
啤酒瓶的爆炸问题是由于啤酒瓶的强度不够引起的,而其最根本的原因在于瓶体微裂纹的存在.在啤酒瓶的使用及回收过程中,剧烈的相互撞击经常发生,频繁的撞击使得啤酒瓶产生微裂纹和疲劳破坏,于是再次使用时只要有一点外界因素(如物理冲击、温度突然改变引起的热冲击等)就会引起破裂或者爆炸,这样的啤酒瓶被人们称为“啤酒炸弹”.本文认为,要使啤酒瓶在使用过程中不产生突然爆炸,危害人身安全,就必须采取措施避免微裂纹的出现和疲劳破坏.为了提高加强环的缓冲性能,可以在环上进行压花处理,使瓶体的相互撞击被加强环缓解掉,避免瓶身其它部位的撞击,这样不仅能够避免微裂纹的出现,也能防止相互撞击产生的疲劳破坏.
[1] GB4544-1996.包装国家标准汇编4[S].北京:中国标准出版社,1997:448-453.
[2] 唐志祥.包装材料与实用包装技术[M].北京:化学工业出版社,1996:576-592.
[3] 陈祖云,曾秉芳.包装材料与容器手册[M].广州:广东科技出版社,1998:510-516.
[4] [美]M·贝克主编,孙荣芳译.包装技术大全[M].北京:科学出版社,1992:92-97.
[5] 金潇明.玻璃瓶的强度分析与计算[J].包装工程,1998,19(3):11-14.
[6] 徐自劳,郑百哲.中国包装工程手册[M].北京:机械工业出版社,1996:287-305.
[7] 刘 工,赵炎为.包装测试技术[M].长沙:湖南大学出版社,1989:256-260.
[8] [日]日本包装技术协会编,菜少玲等译.包装技术手册[M].北京:机械工业出版社,1994:578-584.

