基于Matlab的科里奥利力对抛体运动的影响

王安祥， 李继军， 翟学军， 张晓军

(1.西安工程大学理学院， 陕西 西安 710048； 2.内蒙古工业大学理学院， 内蒙古 呼和浩特 010051)

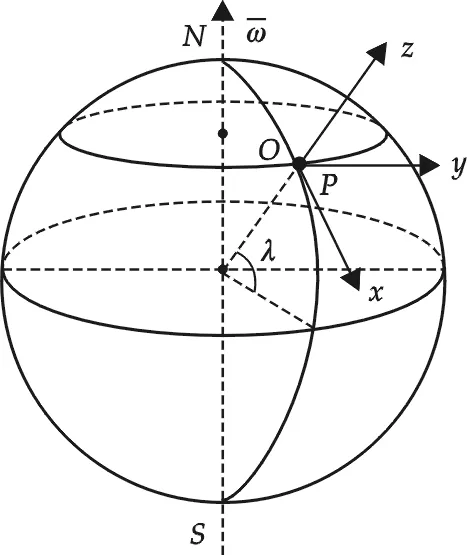
图1 地球表面上的空间转动参照系

0 前 言

地球自转对物体运动的影响主要就是科里奥利力的影响，一些教材上[1-3]只给出了物体自由落体运动的近似结果，在此之前的文献[4-7]多是研究物体自由落体运动和竖直上抛运动，并且大多数忽略了空气阻力.本文将计算不考虑空气阻力时物体自由下落和竖直上抛运动的精确解，并在此基础上计算考虑空气阻力时物体沿任意方向抛射的近似解，以期更为客观、真实地反映科里奥利力对物体运动的影响.

1 不考虑空气阻力情况下物体自由落体运动的精确解

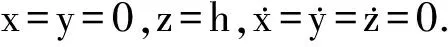
质点在x,y,z 3个方向上的运动微分方程为

(1)

由于物体除受重力外不受其它外力作用，即Fx=Fy=Fz=0，所以质点的动力学方程可简化为

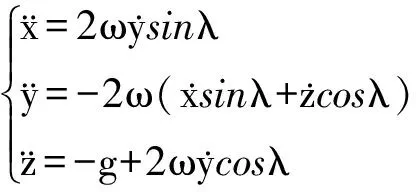
(2)

将(2)式中的第一式和第三式分别对时间积分一次，得

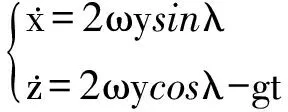
(3)

将上式代入(2)式中的第二式，可得

(4)

上式为受迫简谐运动微分方程，其通解为

(5)

将上式对时间t微分一次，得

(6)

由初始条件即可确定积分常数A和B：

所以得特解：

(7)

再将上式代入(3)式，对时间积分并应用初始条件，即可解得

(8)

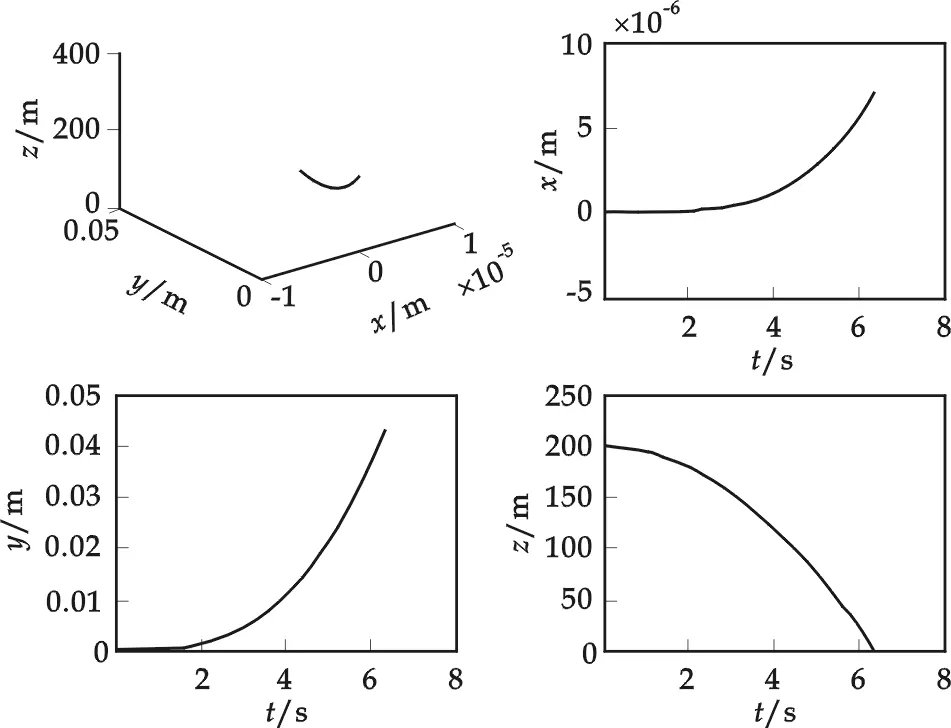
图2 自由落体运动的Matlab模拟

(6)式和(8)式即为在科里奥利力作用下忽略空气阻力时物体自由落体运动的精确解.

假设物体从北纬45°、高度h=200m处自由落下，通过Matlab模拟可得其运动轨迹如图2所示. 从图中可以看出，物体在北半球自由落体过程中，不仅要向东偏移，而且还要向南偏移，但向南偏移的量与向东偏移的量相比要小很多.

2 不考虑空气阻力情况下物体竖直上抛运动的精确解

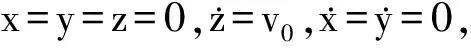
(9)

假设物体从北纬45°、以初速度v0=40m/s将物体竖直上抛，通过Matlab模拟可得其运动轨迹如图3所示. 从图中可以发现，在北半球竖直上抛过程中，物体在上升阶段做偏西运动，在下落阶段仍做偏西运动，因此竖直上抛物体的落地点是偏西的，同时物体还要向北偏移，因此落地点偏向西北方向，但是向北偏移量与向西偏移量相比非常小. 类似地，图4是利用Matlab模拟的在南纬45°以初速度v=40m/s将物体竖直上抛的运动轨迹. 从图中可以看出，在南半球竖直上抛过程中，物体在上升和下落阶段都向西偏移，同时物体还要向南偏移，因此落地点是偏向西南方向的.

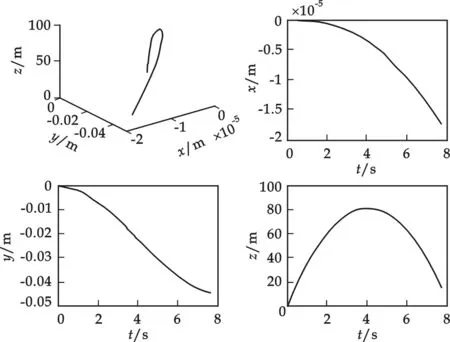
图3 竖直上抛运动的Matlab模拟(北半球)

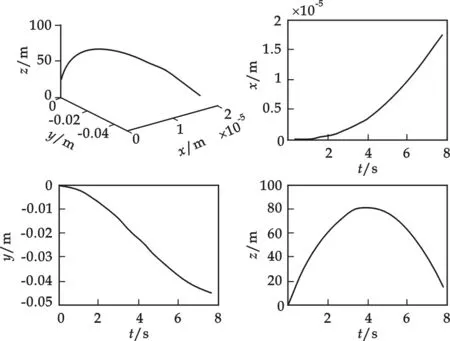
图4 竖直上抛运动的Matlab模拟(南半球)

3 考虑空气阻力情况下的物体斜抛运动的近似解

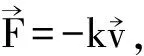
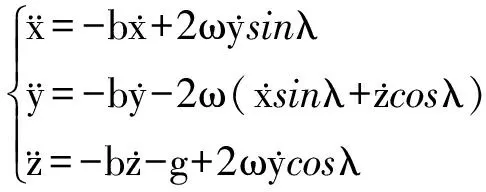
(10)

上式对时间积分一次，代入初始条件得：

(11)

将(11)式整理成下面形式，得

(12)

把(11)式代入(10)式得：

(13)

由于ω2很小，为计算方便，此处略去含ω2的项，则有

(14)

将(12)式代入(14)式，可得

(15)

对上式进行求解，并利用初始条件得：

(16)

上式即为考虑空气阻力情况下物体斜抛运动的近似解.

假设物体从北纬45°、高度h=0m处，以x、y、z 3个轴的分量都是10m/s的初速度抛出，阻力系数b=0.01N·s/(m·kg)，通过Matlab模拟可得其运动轨迹如图5所示.考虑空气阻力下的东西抛射、南北抛射及竖直上抛仅是斜抛运动的特例,下面以南北抛射为例予以说明.

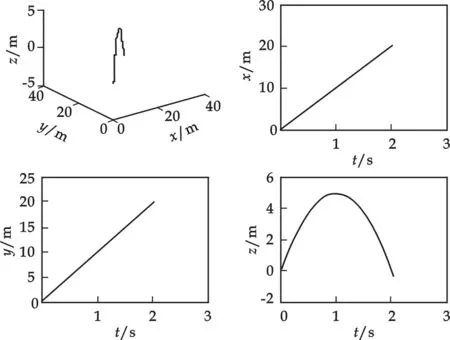
图5 考虑空气阻力下斜抛运动的Matlab模拟

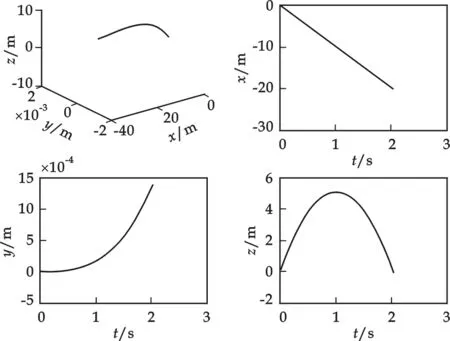
图6 考虑空气阻力下南北抛射运动的Matlab模拟

假设物体从北纬45°、高度h=0m处，以x轴分量是-10m/s、z轴的分量是10m/s、y轴的分量为零的初速度抛出，阻力系数取b=0.01N·s/(m·kg)，通过Matlab模拟可得其运动轨迹如图6所示.

从图6可以看出，在北半球自南向北抛射物体过程中，物体向东发生偏移，也就是向物体运动方向的右侧偏移.因此，在北半球抛体运动中，物体总是向着其运动方向的右侧偏移，然而在南半球抛体运动中则向着其运动方向的左侧偏移.

4 结束语

本文获得了在不考虑空气阻力情况下物体自由下落、竖直上抛运动的精确解，进一步得到了考虑空气阻力情况下物体沿任意方向抛射的近似解，并在Matlab模拟的基础上对所得结果进行了深入分析.这些结果更为客观、真实地反映了科里奥利力对物体运动的影响，更具有普适性.

参考文献

[1] 周衍柏.理论力学教程[M].北京：高等教育出版社，2009:189-191.

[2] 金尚年，马永利.理论力学[M].北京：高等教育出版社，2002:160-166.

[3] 潘武明.力学[M].北京：科学出版社，2004:93-95.

[4] 喀兴林. 落体偏东[J].大学物理，2001，20(7)：6.

[5] 徐水源.科里奥利力对竖直上抛物体运动的影响[J].黄石教育学院学报，2004，21(4):67-71.

[6] 李 拓.自由落体和抛体偏离的另一种解法[J].大学物理，2005，24(3):61-63.

[7] 周永平，刘孜杰.北半球自由落体南偏的一种精确解法[J].大学物理，1994，13(6):1-4.