多约束光学雷达轨迹规划技术
孟中杰,陈凯,黄攀峰,闫杰
(西北工业大学 智能机器人研究中心,陕西 西安710072)
0 引言
根据信号获取方式的不同,可以将现代跟踪系统分为主动式和被动式2 种。以普通雷达为代表的主动跟踪技术和以光学雷达为代表的被动跟踪技术各有优劣[1],普通雷达能够测量高精度的距离信息,而光学雷达可以测量高精度的角度信息,两者配合使用可以对目标的状态进行精确估计。但在很多恶劣的作战环境下,由于无线电静默的要求或受到敌方干扰,普通雷达不能正常工作,光学雷达需要单独对目标进行探测和跟踪。因此,被动跟踪技术一直是目标跟踪领域一个重要的研究方向。
从国内外学者对这个问题的分析研究中发现,光学雷达的单站被动跟踪问题具有强非线性和弱可观测性2 大特点,因此单站跟踪技术的可观测性分析显得异常重要。以文献[2]为代表的大量文献利用理论推导的方法得出观测平台运动方程阶次高于估计目标运动方程阶次,且观测与运动不同向时,目标可观测的结论。但这仅是目标可观测的充分条件,满足此条件时,滤波仍非常容易发散。文献[3]与文献[2]类似,研究了单站纯方位跟踪的可观测性条件,对本文优化目标函数的建立有重要的指导意义。文献[4]使用EKF 滤波,利用量测估计值的FISHER 信息量和罗美达下界的迹tr(CRLB),作为优化目标,对匀速运动目标进行跟踪,实现观测器的轨迹优化,并得出结论:使用罗美达下界进行优化时,滤波结果的位置误差较小。文献[5]提出基于P阵和CRLB 的优化函数,提高了状态估计精度。但这些研究均没有考虑对被动跟踪问题至关重要的载机机动能力、光雷探测范围等约束条件。文献[6]研究了伪线性卡尔曼滤波,对本文有很大的参考作用。文献[7 -8]提出了2 种新式的滤波算法,但计算量过大,不适用于实时计算。
本文充分考虑光学雷达的探测范围/探测周期、载机机动能力、目标进入角、载机/目标巡航高度差等多个约束,建立针对运动目标单站跟踪问题的轨迹规划模型,设计一种tr(P)与det (FIM)相结合的目标函数,采用伪线性卡尔曼滤波进行轨迹优化,最后在多种空战态势下进行了仿真分析。仿真表明:该方法生成的飞行轨迹能够满足载机机动能力和光学雷达探测能力的要求,状态估计速度快,精度高。
1 光学雷达被动跟踪模型的建立
在大地系下,建立光学雷达单站跟踪的数学模型。首先定义k 时刻目标状态为XT(k),光学雷达测量值为YT(k).

其中,xT(k),yT(k),zT(k)为目标的三向位置状态,vxT(k),vyT(k),vzT(k)为目标的三向速度状态;α(k)和β(k)分别为光学雷达纵向与侧向的测量角。为表达简便,将式(1)简写为

定义XC(k)为载机k 时刻状态。建立光学雷达单站跟踪的数学模型如式(3)所示。其中,q(k)为模型噪声;N(k)为量测噪声;Φ(k,k -1)为状态一步转移矩阵;T 为光学雷达探测周期。
对于这样一个状态方程线性、量测方程非线性的系统,可以采用UKF 或EKF 等先进的滤波算法进行滤波计算,但这些滤波方法计算量较大,为减小了计算量,本文选用伪线性卡尔曼滤波算法进行滤波计算。
将量测方程伪线性化为方程(4),推导伪线性卡尔曼滤波方程如式(5)所示。
针对建立的光学雷达被动跟踪模型,利用伪线性卡尔曼滤波技术可以估计出光学雷达单站跟踪时的目标位置/速度信息。初值选择采用探测范围内随机赋值的方法。



2 光学雷达载机飞行轨迹规划
只要光学雷达载机的运动阶次不低于目标的运动阶次,且两者运动不同向时,按照本文建立的光学雷达观测模型,即可估计出目标的位置[2]。但是光学雷达单站跟踪问题是一个弱可观测问题,按照上述充分条件飞行时,可观测度仍较低,位置估计的准确度也较低,且有可能滤波发散。因此,需要规划合理的载机飞行轨迹,使光学雷达能够较好的估计出目标的位置信息。
在实际飞行中,载机机动能力与光学雷达的探测范围是严格受限的,从而使载机的飞行轨迹受到了极大的限制;且在滤波过程中,一旦出现探测不到目标的情况,光学雷达就会马上脱离“跟踪”模式,进入“搜索”模式,造成目标估计失败。因此,在轨迹规划过程中,首先需要分析载机的实际可飞区域。
假设载机巡航飞行为匀速运动,巡航速度为v0,可用过载为nx,载机可连续机动时间间隔为TC,探测范围为±βT,载机航向角为φ,光学雷达视场中线与X 轴的夹角为β.由于机动能力限制,载机每次机动时的最大转弯角度βC为

经推导,载机每次机动时可选飞行区域为

下面研究光学雷达轨迹规划目标函数的设计问题。滤波每一步计算的P 阵反映了目标的运动信息,所以可以将P 阵的迹(tr(P))作为优化目标之一;当滤波的FISHER 信息量的行列式较大时,系统可观测性较强,滤波方差较小,因此将det (FIM)也作为优化目标之一。
在目标可观测的前提下,量测角变化越快,系统可观测度越高,收敛速度越快,收敛精度越高[2-3]。对光学雷达单站跟踪问题进行进一步分析和初步的仿真发现:基于P 阵的优化目标函数主要通过减小目标与载机间的距离,来加速量测角的变化;而基于FISHER 信息量的优化目标函数主要以载机机动的方式来增加量测角的变化;因此,设计优化目标函数如下

P 阵在滤波的每一步计算时可以得到,下面推导滤波的FISHER 信息量FIM.
量测角的分布函数为[4]

将式(3)、式(4)联立,可以解出滤波的FISHER信息量:
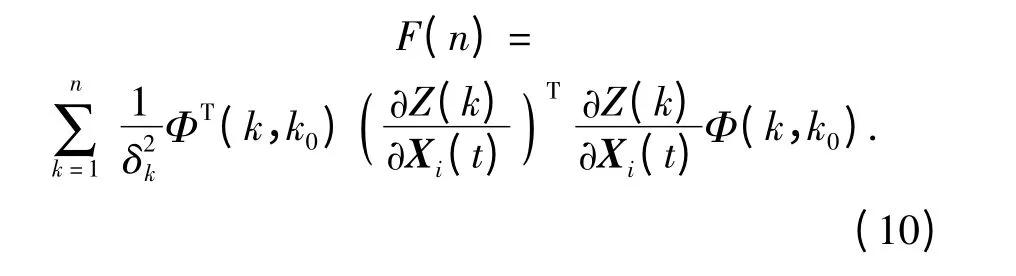
将式(10)写成递推形式得:

为提高规划速度,将全局优化问题简化为局部优化问题,选择动态规划法规划飞行轨迹。光学雷达载机飞行轨迹规划流程如图1所示。
3 仿真分析
为验证本文推导的光学雷达被动跟踪模型和设计的轨迹规划策略,设置仿真初始条件如表1所示;光学雷达及系统噪声指标设置如表2所示。
滤波初值的选择采用无先验信息的随机分布。利用本文设计的轨迹规划思路,规划出载机最优飞行轨迹。目标与载机运动态势、估计的目标位置如三维图2所示。飞行全程光雷视线角,飞行过程需用过载如图3所示。从图2、图3可以看出,算法规划出的飞行轨迹是一个类似“S”型的轨迹,这条轨迹使光学雷达的视线角先变到正最大允许值,再变到负最大允许值,变化的速率和飞行过程中的可用过载成一定的对应关系。

表1 仿真初值Tab.1 The initial value for simulation

表2 光学雷达及系统噪声指标Tab.2 The noises of optical radar and system
载机按照规划出的轨迹飞行,目标状态估计的误差曲线如图4、图5所示。由仿真结果可以看出目标位置和速度的估计非常准确,精度极高,且滤波收敛较快,仅需50 s 左右。

图2 飞行态势及跟踪效果曲线图(迎头)Fig.2 The flying state and track result (head on)

图3 优化得到的航迹及载机状态Fig.3 The trajectory and state after optimization

图4 目标位置估计误差Fig.4 Estimation error of the target location
更改飞行态势为尾追,通过本文的方法规划出飞行态势如图6所示。可以看出,规划出的轨迹依然是一个类似“S”型的轨迹,这条轨迹使光学雷达的视线角先变到正最大允许值,再变到负最大允许值。通过改变目标变速度、目标机动、迎头/尾追等多种态势的仿真分析,均可以得出同样的结论。这个结论可以使载机在由于某种故障无法进行航迹规划时,由驾驶员操纵载机进行飞行,最大限度的保证光学雷达的观测效果。这些仿真也验证了经本文的规划策略规划出的飞行轨迹能够在满足载机机动能力和光学雷达探测范围的基础上,尽快地估计出目标位置、速度等诸参数,而且算法的计算量较小,鲁棒性强。
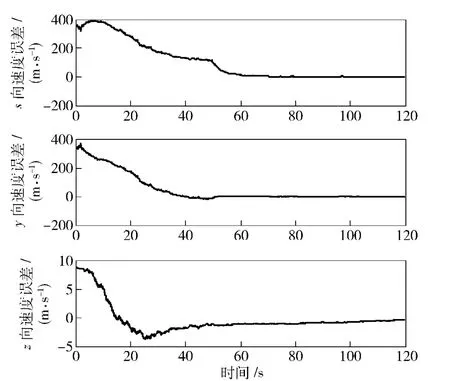
图5 目标速度估计误差Fig.5 Estimation error of the target speed
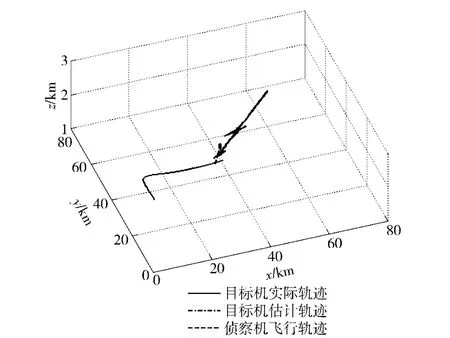
图6 飞行态势及跟踪效果曲线图(尾追)Fig.6 the flying state and track result (trail guidance)
4 结束语
本文考虑光学雷达的探测范围/探测周期,载机机动能力,巡航高度差等多种强约束条件,建立了光学雷达单站跟踪问题的轨迹规划模型,设计了一种tr(P)与tr(CRLB)相结合的目标函数,采用分段优化策略规划强约束条件下光学雷达被动跟踪的载机最优飞行轨迹。仿真结果表明:该方法规划的飞行轨迹满足载机机动要求和光学雷达的探测要求,光学雷达被动跟踪速度较快,估计精度高。
从光学雷达的视线角看,规划的轨迹使光学雷达的视线角以20°~60°~-60°的变化规律变化,类似于对固定目标的S 形机动。因此,实战中,若侦察机无法进行航迹规划时,可以按照视线角的这种变化规律飞行,提高目标观测效果。
本文的跟踪模型是在目标匀速巡航的假设下建立,目标机动情况下的光学雷达轨迹规划技术值得进一步研究。
References)
[1]郭云飞.纯方位角目标跟踪理论与应用研究[D].杭州:浙江大学,2007.GUO Yun-fei.Theory and application research on bearing only target tracking[D].Hangzhou:Zhejiang University,2007.(in Chinese)
[2]Jauffret C,Pillon D.Observability in passive target motion analysis[J].IEEE Transon Aerospace and Electronic Systems,1996,32(4):1290 -1300.
[3]杨国胜,窦丽华,侯朝桢.基于纯角度的三维运动目标可观性研究[J].兵工学报,2004,25(2):182 -185.YANG Guo-sheng,DOU Li-hua,HOU Chao-zhen,Observability criteria based on bearing-only measurements for three-dimensional moving targets[J].Acta Armamentarii,2004,25(2):182 -185.(in Chinese)
[4]Le Cadre J P,Michel S L.Optimizing the receiver maneuvers for bearings-only tracking[J].Elsevier Science on Automatic,1999,35(5):591 -606.
[5]张益.被动式跟踪轨迹优化算法研究[D].西安:西北工业大学学位论文,2005.ZHANG Yi.The study on optimizing trajectory in passive tracking[D].Xian:Northwestern Polytechnical University,2005.(in Chinese)
[6]辛云宏,杨万海.基于伪线性卡尔曼滤波的两站红外无源定位及跟踪技术[J].西安电子科技大学学报,2004,31(4):505-508.XIN Yun-hong,YANG Wan-hai.Pseudo-linear Kalman filter based passive location and tracking techniques by two infrared stations[J].Journal of Xidian University,2004,31(4):505 -508.(in Chinese)
[7]马野,王孝通,李博,等.舰船导航信号非线性UKF 滤波定位解算方法研究[J].兵工学报,2007,28(5):539 -542.MA Ye,WANG Xiao-tong,LI Bo,et al.Positioning algorithm for ship's navigation signal based on nonlinear UKF[J].Acta Armamentarii,2007,28(5):539 -542.(in Chinese)
[8]杨争斌,郭福成,周一宇.基于UT 变换的机动辐射源单站被动跟踪IMM 算法[J].系统工程与电子技术,2007,29(1):5-8.YANG Zheng-bin,GUO Fu-cheng,ZHOU Yi-yu.Maneuve ring emitter tracking with a single passive observer using IMM algorithm based on unscented transformation[J].Systems Engineering and Electronics,2007,29(1):5 -8.(in Chinese)
——2022 F1意大利大奖赛

