涵道式无人机鲁棒控制系统设计

李远伟， 王常虹， 伊国兴， 奚伯齐

（哈尔滨工业大学空间控制与惯性技术研究中心，黑龙江哈尔滨 150080）

0 引言

具有自主飞行能力的小型涵道式无人机，可用于航拍、桥梁检测、交通监控、资源调查、低空突防、空中巡逻、反恐救援、情报搜集和敌方战场搜救等任务［1］，具有广泛的军事、民用和科学研究价值。本文所研究的小型涵道式无人机采用环道螺桨升力装置和涵道导流系统抗扭技术，具有如下特点:①结构紧凑、机动灵活，可以完成垂直起降、悬停、高速飞行等一系列特殊动作;②推进效率高;③噪音低、隐蔽性好，涵道的存在降低了风扇的气动噪声，提高了螺旋桨使用的安全性。

目前世界上多个国家把具有垂直起降功能的涵道式无人机作为研究的重点，其中最具代表性的是Allied Aerospace公司的 i-STAR 涵道无人机［1－2］，霍尼韦尔公司的Kestrel涵道无人机也完成了试飞，目前在各种恶劣环境下进行测试以测定该无人机的使用范围。除此之外，新加坡也推出了自己的涵道风扇无人机Fan-tail。国内对涵道式无人机的研究起步较晚，还停留在对涵道风扇系统的气动特性研究中，南京航空航天大学通过风洞实验分析了涵道风扇升力系统的升阻特性，指出涵道风扇作为升力装置仅适合于强调悬停和低速飞行性能的飞行器，对涵道式无人机的设计和应用有很大的指导意义［3－4］。但是对于控制方法应用于涵道式飞行器飞行试验目前鲜有研究成果报道。

本文将结合小型涵道式无人机的研制过程来分析涵道式无人机的建模与控制问题，并将其应用于飞行试验。首先，建立精确的数学模型对于控制系统设计有很大的帮助，但是涵道风扇式无人机具有独特的气动外形导致周围流场的分布很复杂［5］，目前还没有成熟的理论分析和计算方法，因而基于刚体动力学建立的数学模型与实际模型具有很大的偏差，这就要求控制器具有很强的鲁棒性。在涵道式无人机控制问题上，目前大多将PID控制应用于飞行试验，它能够满足悬停和小范围机动;但是对于大攻角高速前飞时，往往会由于外界的干扰和模型参数的时变性使系统变得不稳定。本文将H∞理论应用于控制器设计中，以提高系统的鲁棒稳定性和抗干扰性。

1 涵道式无人机动力学分析

涵道式飞行器结构如图1所示，包括上载荷仓、涵道风扇系统、下载荷仓和着陆架等4部分，其中上载荷仓用来装载有效载荷，涵道中间为发动机，下载荷仓用来装载电子设备，如飞行控制器等。飞行姿态由对称分布在涵道尾部的四组舵片控制，高度由螺旋桨转速决定;因此，无人机所受到的力主要来自于以上各组成部分的空气动力和重力，飞行器所受到的力以及力矩为

式中:Faero，Maero分别为机体空气动力和力矩;Frotor，Mrotor分别为旋翼空气动力和力矩;Fduct，Mduct分别为涵道空气动力和力矩;Fvane，Mvane分别为控制舵面空气动力和力矩;Fgrav为重力;Mgyro为陀螺力矩。下面将给出各组成部分的动力学分析。

图1 涵道式无人机结构Fig．1 Configuration of the ducted fan UAV

1.1 机体空气动力分析

机体主要包括上载荷仓，涵道，下载荷仓和起落架等4部分，各自所受的空气动力可以表示为

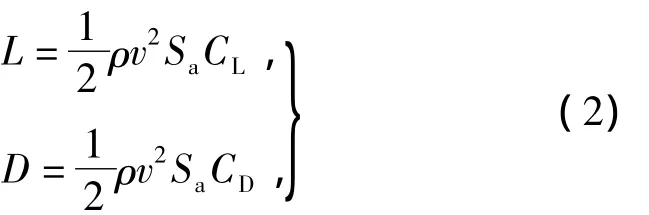
式中:ρ为空气密度;CL，CD分别为无量纲的机体阻力和升力系数，与机体的攻角有关;Sa为机体特征面积。

1.2 涵道风扇推力系统空气动力分析

涵道的存在提高了螺旋桨的气动性能，并且提高了使用安全性，与孤立螺旋桨相比，在相同功率、相同直径时，可产生较大的拉力。在相同功率下产生相同拉力时需要的直径较小，原因在于:涵道的存在改变了螺旋桨下游的滑流状态，增大了滑流面积，减小了滑流速度和滑流动能损失，从而较多地将螺旋桨桨盘后面的动能转化为压力能;涵道壁面改善了螺旋桨桨尖区域的绕流特性，减小了将建损失;涵道的入口前缘形成了较大的负压区，产生了附加拉力。设T为涵道风扇系统总拉力，Ts为涵道拉力，Tp为螺旋桨拉力，因此

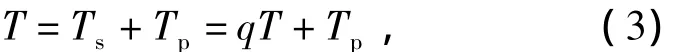
其中q为涵道拉力比例因子，q=Ts/T。涵道拉力因子q理论公式可用，目前主要利用R．Kriebel关于薄圆柱涵道螺旋桨的研究成果，螺旋桨拉力Tp和总拉力T之比的近似为

根据涡流理论推导出螺旋桨产生的拉力和螺旋桨反扭矩分别为［6］

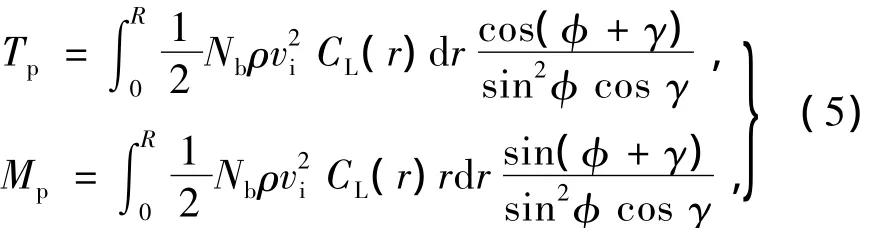
式中:vi为诱导速度;Nb为桨叶数量;ωp为旋翼转速;CL（r）为旋翼无量纲升力和阻力系数，与r有关，r表示叶素所在的位置到桨轴的距离。由此可以计算出涵道风扇系统产生的总拉力。

当无人机前飞或存在侧风的情况下的悬停时，涵道处于横向来流和涵道风扇轴向吸流的综合作用之下，涵道周围流场分布不均匀，横向气流通过涵道后方向改变为沿涵道轴向流动，会对机体产生阻力和俯仰力矩［7］，即

1.3 控制舵面空气动力分析

控制舵面的空气动力为

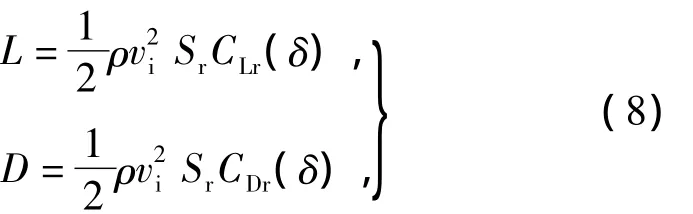
式中:Sr为控制舵面特征面积;CLr，CDr分别为控制舵面的无量纲升力和阻力系数，与舵面的偏转角δ有关。

控制舵面的分布如图2所示，控制量分配为δ1= δp+ δr，δ2= δq－ δr，δ3= δp－ δr，δ4= δq+ δr，（9）式中:δp，δq，δr分别为横滚、俯仰、偏航控制量;δ1，δ2，δ3，δ4分别为各组舵片的偏转角度。

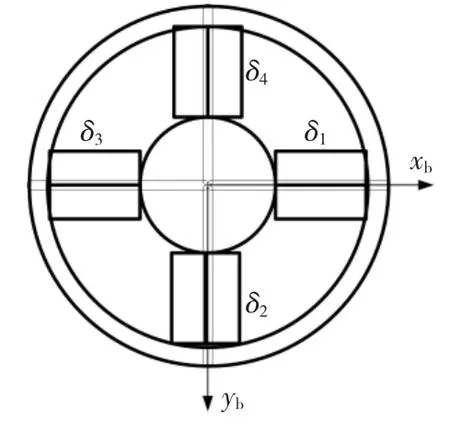
图2 控制舵片分布Fig．2 Configuration of control vanes

1.4 重力

机体所受到的重力为

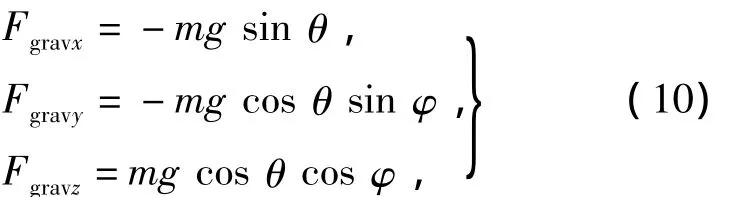
其中m为机体质量。

1.5 陀螺力矩

螺旋桨的选装会带来陀螺力矩，由

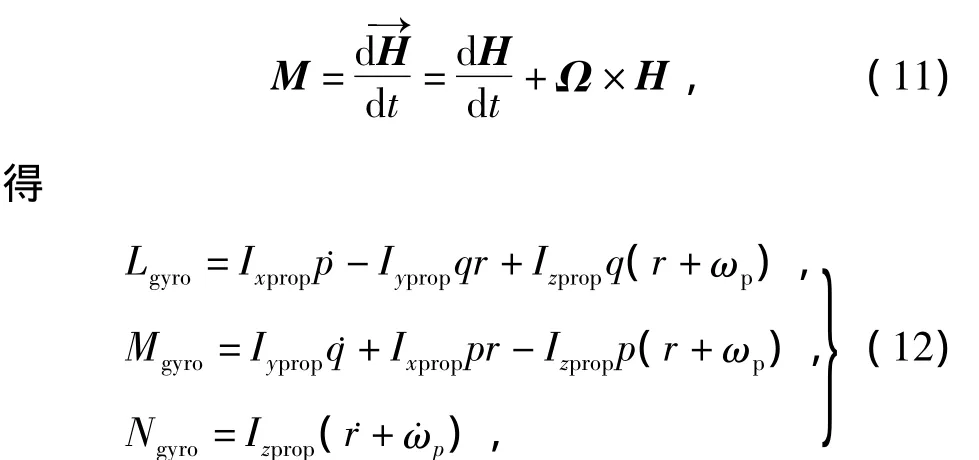
式中:ωp为螺旋桨转速;Ixprop，Iyprop，Izprop分别为螺旋桨转动惯量。由于Ixprop=Iyprop≈0，在稳定控制阶段˙ωp≈0、˙r≈0，可以得到由陀螺力矩效应产生的耦合力矩

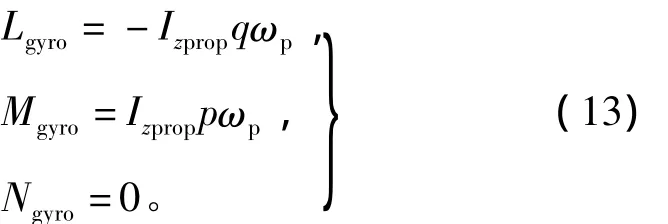
2 模型简化

无人机系统为一多输入多输出系统，各个通道之间存在耦合，要对各个通道单独控制，必须对系统进行解耦。假设各控制舵片之间不存在相互干扰，除了陀螺力矩效应之外，不存在其它耦合，由式（13）可得的解耦方法［8］如图3所示。

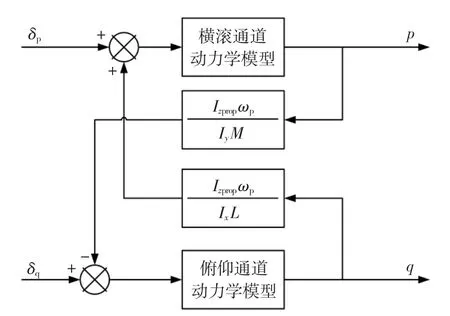
图3 解耦框图Fig．3 Decoupling block diagram

通过解耦得到以下各通道的模型。

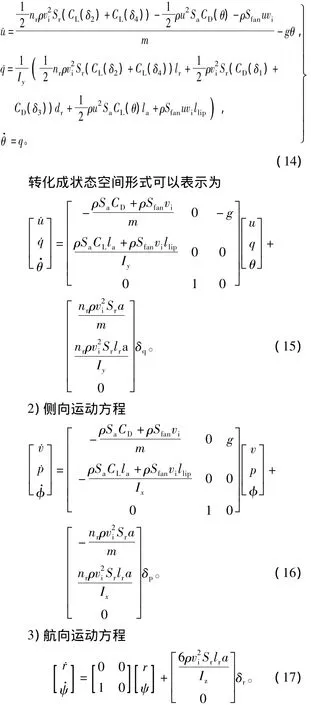
1）纵向运动方程

在悬停稳定控制阶段，姿态角度变化范围小，因而控制舵片偏转角度小。假设在小角度范围内控制舵片的升力系数和阻力系数与偏转角度呈线性关系，即 CL（δ）=aδ、CD（δ）=bδ，在此假设无人机质心与机体气动力中心处于同一水平面上，则纵向通道运动方程可以简化为

4）垂直运动方程

在悬停时，高度由油门开度控制，假设在悬停时，旋翼转速为ω0，对应油门开度为δe0，则

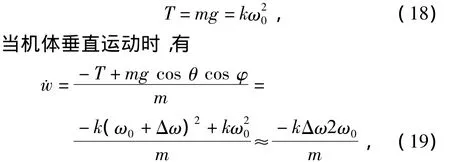
因此高度控制就可以转化为旋翼转速的控制，垂直方向运动的状态空间表达式为

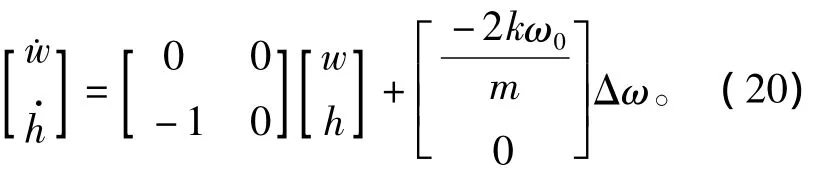
3 控制系统设计

本文所研究的涵道式无人机具有质量小、结构紧凑、惯量小等特点，导致它更容易受到外界干扰。涵道式无人飞行器具有独特的气动外形，其气动特性与传统的固定翼飞行器不同，周围流场分布复杂，动力学方程具有非线性、不确定等特征;因此姿态控制器必须具有较强的鲁棒性，设计控制器时需考虑如下干扰和参数不确定性。

3.1 干扰分析

涵道式无人机所受到的干扰主要来自于自然界的风。考虑风的干扰时，纵向运动方程为

3.2 参数不确定性

在实际应用中，无人机随着高度不同、飞行速度不同，以及负载引起的重心变化等都会导致部分气动参数的大范围变化，导致部分模型参数发生大范围的摄动。参数不确定性主要来源于模型线性化误差、无人机转动惯量的计算误差以及气动参数的时变性等。文献［9］中指出相邻控制舵片间无干扰的最小距离，而在结构设计中很难达到要求，同一组控制舵片之间必然存在的相互影响，它们之间的干扰无法准确计算，因此在动力学分析时会产生误差［9］。

考虑参数不确定性，被控对象描述为

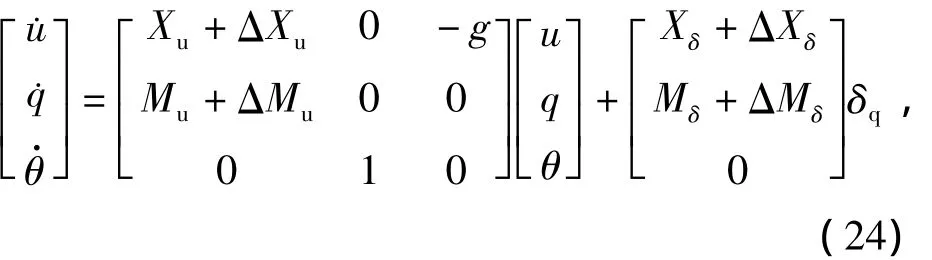
其中 ΔXu，ΔMu，Δg，ΔXδ，ΔMδ分别为各参数的摄动参数。

为了保证飞行器控制性能，当参数变化时，飞行姿态仍能保持稳定，即设计反馈控制器，使得参数在一定范围内变化时，系统仍能保持稳定。

3.3 鲁棒控制器设计

鲁棒H∞控制器研究参数摄动情况下的扰动抑制问题，使得系统在有外部干扰和参数摄动的情况下仍能保持稳定［9］。

考虑被控对象

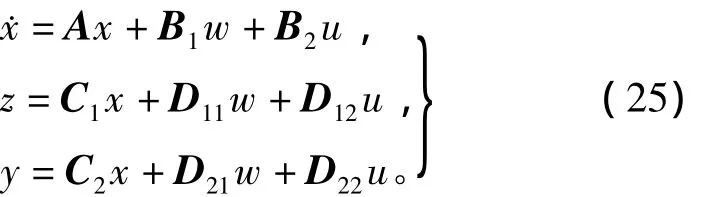
定义1 H∞标准控制问题:对于给定增广被控对象，判断是否存在反馈控制器K（s），使得闭环系统内部稳定且‖Tzw‖∞＜1。如果存在那样的控制器，则求之。

定理1 对于系统（25），存在一个状态反馈H∞控制器，当且仅当存在一个对称正定阵X和矩阵W，使得矩阵不等式

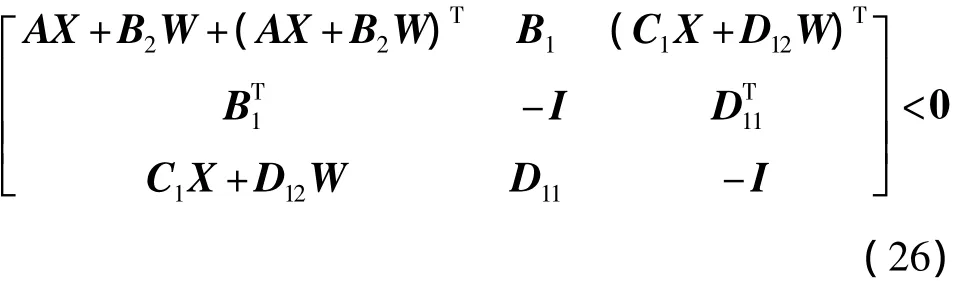
成立。进而，如果不等式（26）存在一个可行解X、W，则u=WX－1x是系统（25）的一个状态反馈H∞控制器［10］。

引理1［10］对称矩阵满足

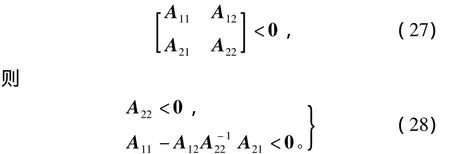
引理2［10］给定适当维数的矩阵Y、D和E，其中Y是对称的，则

对所有满足FFT＜I的矩阵F成立，当且仅当存在一个常数ε＞0，使得

针对涵道式无人机的参数不确定性和干扰抑制问题，需要设计同时满足鲁棒稳定性和干扰抑制性能要求的控制器，被控对象如下:

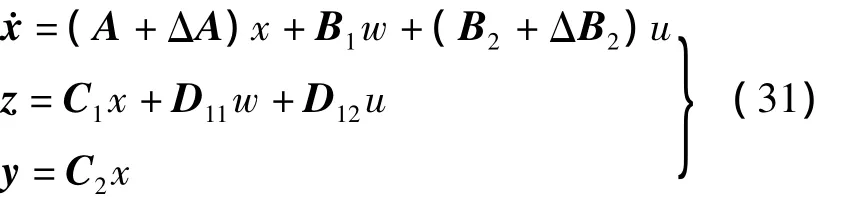
通过求解线性矩阵不等式（35）得到X和W，利用K=WX－1得到满足性能指标的状态反馈控制器 K［11］。

4 数学仿真

以无人机纵向运动为例，代入飞行器参数，得到含参数不确定性的线性化模型

通过解式（35）所对应的矩阵不等式得到满足要求的控制器为

将得到的控制器带入原非线性模型中进行仿真，在干扰输入端加入白噪声，并在第10 s加入了持续时间为10 s的4 m/s的侧风常值干扰。图4为鲁棒控制与PID控制系统仿真结果的比较。其中在PID控制作用下飞行器姿态能够很好的跟踪姿态指令，在10 s处加入4 m/s常值侧风干扰后系统能在较短时间内恢复稳定。当常值干扰取消后也能迅速恢复稳定，但是对于噪声干扰的抑制效果有限。在鲁棒控制器作用下，系统能够很好的跟踪姿态指令，在10 s处加入侧风干扰后系统能在较短时间内恢复稳定，当常值干扰消失后也能迅速恢复稳定，说明该控制器具有很强的鲁棒性，并且可以看出此时系统对噪声干扰具有很好的抑制效果。

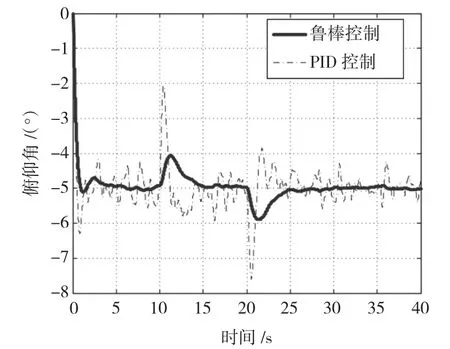
图4 鲁棒与PID控制仿真结果比较Fig．4 Comparison between robust controller and PID controller

为了验证控制器在参数变化时系统的鲁棒稳定性，在质量和转动惯量发生改变（±30%）时的仿真结果如图5所示。

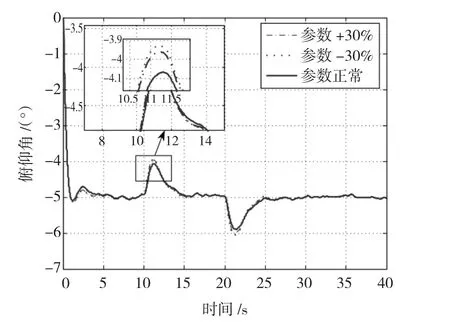
图5 参数变化时鲁棒控制仿真曲线Fig．5 Simulation of robust controller with parameter variation

由图5可以看出，当质量和转动惯量发生改变时系统的仍然具有很好的稳定性以及跟踪性能，验证了该控制器具有较好的鲁棒性，下面将进一步通过飞行试验来验证。

5 飞行试验研究

试验条件:西南风2.6 m/s（1 min内平均值）。为了验证控制系统的鲁棒性，在原机体质量的基础上装载500 g负载。飞行试验结果如图6～图8所示。

从图7可以看到，采用PID控制器时，系统对15°以内俯仰姿态角指令具有较好的跟踪性能，当超过范围时就会存在较大的跟踪误差，同时在悬停时姿态系统对于噪声干扰的抑制作用有限，由图8看出，采用鲁棒控制时系统对25°范围内俯仰姿态角指令具有较好的跟踪性能，对噪声干扰的抑制能力明显增强，由此可以得出控制器具有很强的鲁棒性和抗干扰性。

图6 飞行试验Fig．6 Flight testing of the UAV

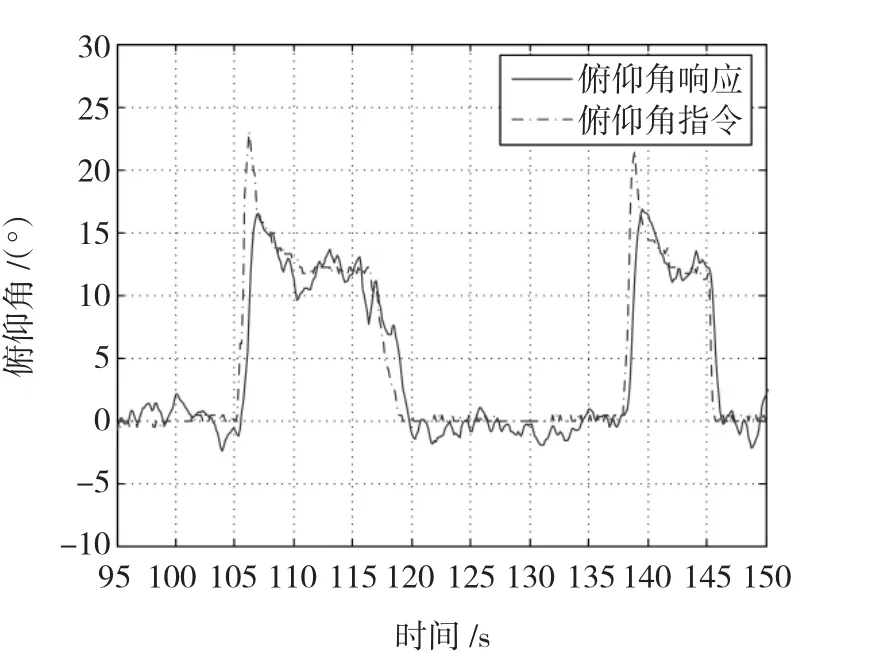
图7 PID控制俯仰姿态角响应Fig．7 Response of Pitch Attitude for PID controller

图8 鲁棒控制俯仰姿态角响应Fig．8 Response of pitch attitude for robust controller

6 结论

经过仿真和实际飞行试验验证了控制算法的有效性。飞行试验结果表明，通过解耦后设计经典PID控制器能够保证无人机在悬停以及小角度机动飞行中的快速准确的姿态跟踪性能，但是对于大攻角高速前飞时系统的稳定性不能保证，而采用鲁棒控制时系统的稳定性得到了大大的提高，同时对噪声干扰的抑制能力大大加强。

［1］LARRY L，JASON D，MARK B．The micro craft iSTAR air vehicle:control system design and testing［C］∥American Helicopter Society57th Annual forum．Washington DC:American Helicopter Society International，2001:1 －11．

［2］ CHRISTINA M，MOHAMMADREZA H，MARK B，et al．Nonlinear inversion control for a ducted fan UAV［C］∥AIAA Atmospheric Flight Mechanics Conference and Exhibit．San Francisco，California:American Institute of Aeronautics and Astronautics，2005:1－26．

［3］李建波，高正，唐正飞，等．涵道风扇升力系统的升阻特性试验研究［J］．南京航空航天大学学报，2004，36（2）:164－168．

LI Jianbo，GAO Zheng，TANG Zhengfei，et al．Experimental investigation on lift and drag of ducted fan system［J］．Journal of Nanjing University of Aeronautics＆Astronautics，2004，36（2）:164－168．

［4］李建波，高正．涵道风扇空气动力学特性分析［J］．南京航空航天大学学报，2005，37（6）:680－684．

LI Jianbo，GAO Zheng．Aerodynamical characteristics analysis of ducted fan［J］．Journal of Nanjing University of Aeronautics＆Astronautics，2005，37（6）:680 －684．

［5］ GUERRERO I，LONDENBERG K，GELHAUSEN，et al．A powered lift aerodynamic analysis for the design of ducted fan UAVs［C］∥2ndAIAA UAV Conference．San Diego:AIAA，2003:1－8．

［6］刘沛清．空气螺旋桨理论及其应用［M］．北京:北京航空航天大学出版社，2006．

［7］FLEMING J．Improving control system effectiveness for ducted fan VTOL UAVs operating in crosswinds［C］∥AIAA Unmanned Unlimited Systems，Technologies，and Operations．San Diego，California:AIAA，2003:1－11．

［8］DANIEL N．Comprehensive system identification of ducted fan UAVs［D］．San Luis Obispo，CA:California Polytechnic State U-niversity，2004．

［9］MATTIAS E．Performance estimation of a ducted fan UAV［D］．Link Ping，Sweden:Avdelning Institution Division，Department of Electrical Engineering．2006．

［10］申铁龙．H∞控制理论及应用［M］．北京:清华大学出版社，1996:112－123．

［11］俞立．鲁棒控制——线形矩阵不等式处理方法［M］．北京:清华大学出版社，2002:44－45．

（编辑:张静）